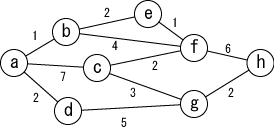
「グラフ(graph)」とは「ノード(節点、node)」を 「エッジ(辺、edge)」で結んだものです。 「ノード」は「頂点(vertex)」、「エッジ」は「枝(branch)」と呼ばれることもあります。
グラフの例を図1に示します。 図の中で「ノード」はアルファベットに丸で、「エッジ」はノードをつなぐ 線で表現されています。 エッジの近くの数字は、エッジの重み(次の問題では「ノード間の距離」)です。
 |
| 図1:グラフの例 |
図1のグラフは表1の隣接行列で表現できます。 ここで、行列の各要素は、ノード間にエッジがある場合はその「重み」に、 ない場合は「-」になっています。 また、同一ノードの間の重みは0であるとしています。
| 表1: 隣接行列 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
いくつかの都市と、それらの都市をつなぐ道路の距離が与えられている。 出発地点と目的地点が与えられたとき、最短経路を探すプログラムを 作りなさい。
$N$ $R$
$A_1$ $B_1$ $L_1$
$A_2$ $B_2$ $L_2$
$\quad\cdots$
$A_R$ $B_R$ $L_R$
$S$ $D$
最初の行には2個の整数 $N$ と $R$ が含まれる。 $N$ は都市の数を表し、 $R$ はそれらの都市をつなぐ道の個数を表す。
$1 \leqq N \leqq 100$
2行目以降は $R$ 行に渡って、3個の整数
$~~$ $A_i$, $B_i$, $L_i$ $~~$ ($1 \leqq i \leqq R$)$~~$
が含まれる。
$A_i$ と $B_i$ は道の両端の都市を表し、$L_i$ は道の距離を表す。
$0 \leqq A_i \leqq N-1$
$0 \leqq B_i \leqq N-1$
その次の行に2個の整数 $S$, $D$ が含まれる。 $S$ は出発地点の都市を表し、$D$は目的地点の都市を表す
$0 \leqq S \leqq N-1$
$0 \leqq D \leqq N-1$
答が発見された場合は次のように出力しなさい。
最初の行に「最短経路の距離」を表す整数を出力し、
次の行に「 最短経路を辿ったときの都市を、出発地点から
目的地点まで順にスペースを1個ずつあけて」出力しなさい。
最短経路が複数ある場合は、そのうちの1つの経路を答えとすればよい
ものとする。
答えが無い場合は、"No route"と出力しなさい。
ダイクストラ法とは、各ノードへの最短経路を、始点の周辺から1個所ずつ 確定し、徐々に範囲を広げていく方法です。 グラフ中の全てのエッジの重みが0以上のときに利用できます。
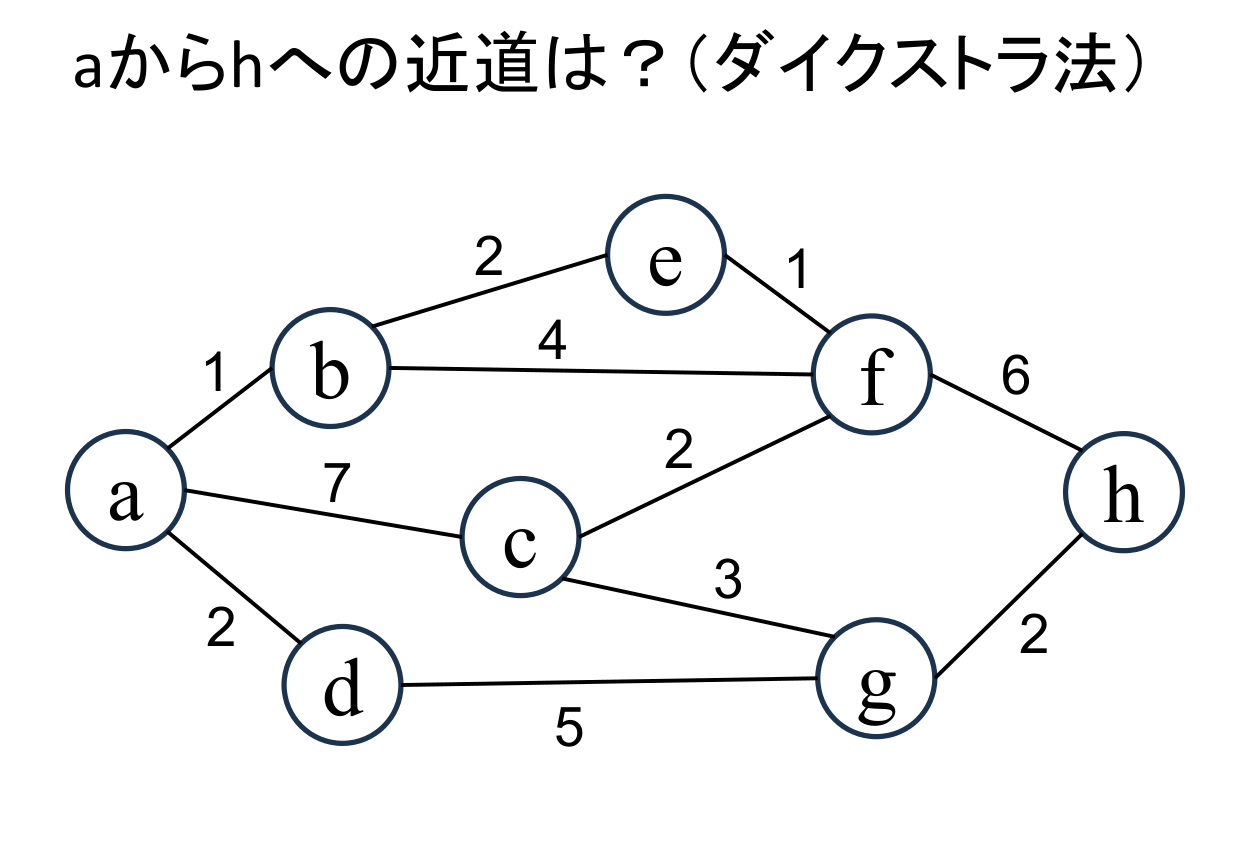 |
出発地点をa、目的地点をhとして、最短経路を通った場合の距離を求めましょう。 |
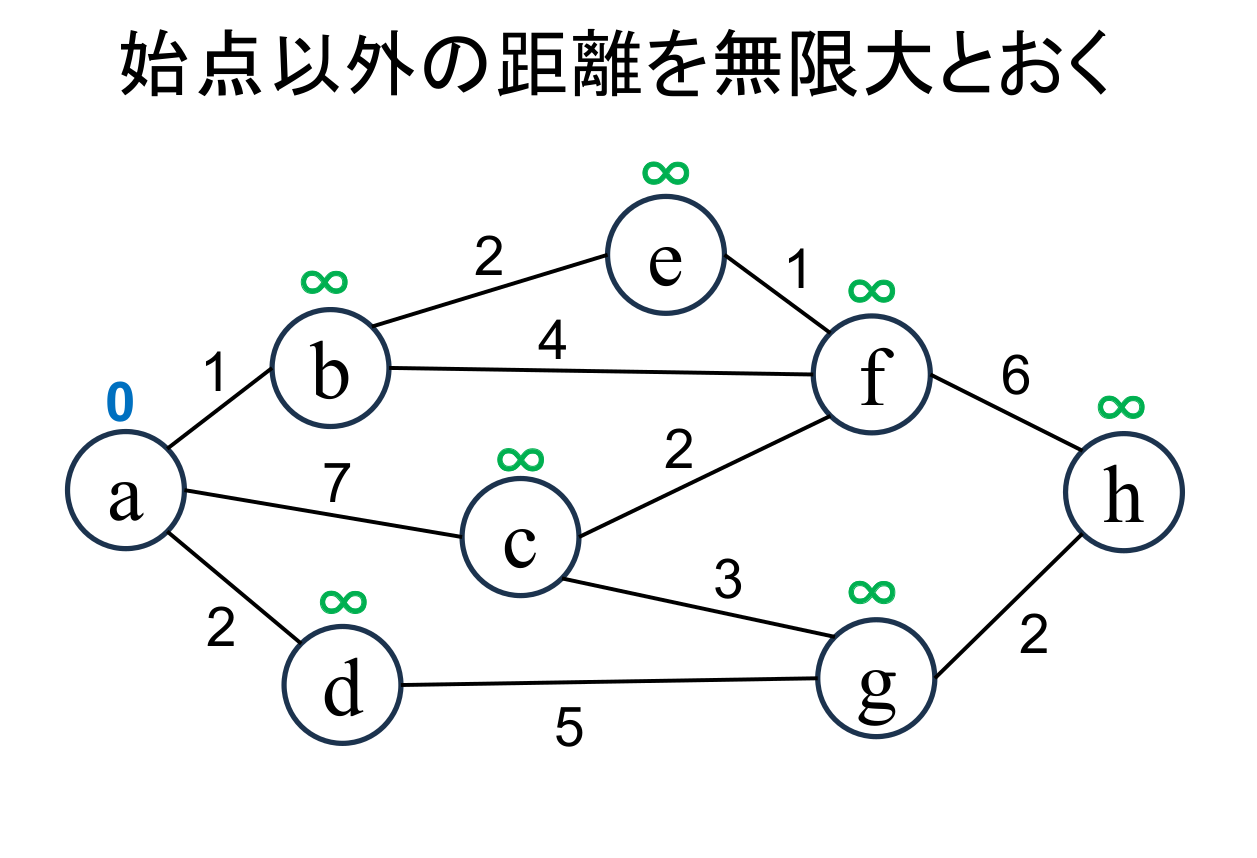 |
全ての地点までの距離を未確定とし、とりあえず無限大 (∞)としておきます。 その上で、出発地点(a)までの距離を0とします。 |
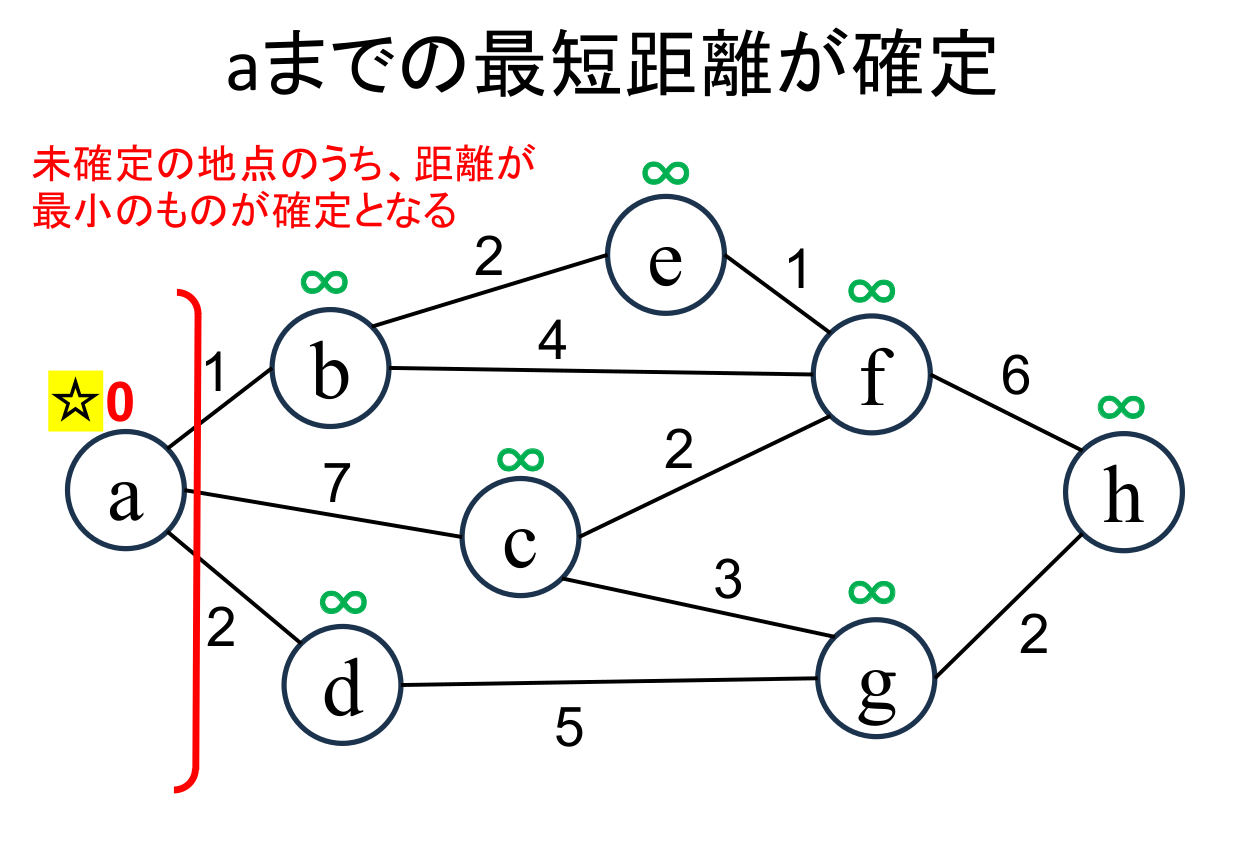 |
未確定の中から距離が最も小さい地点(a)を選んで、 現在の値(0)をその地点の最小距離として確定します。 直近で確定した地点は☆印 をつけて表しています。 確定した地点は、赤い境界線(フロンティア, frontier)で囲んで表しています。 |
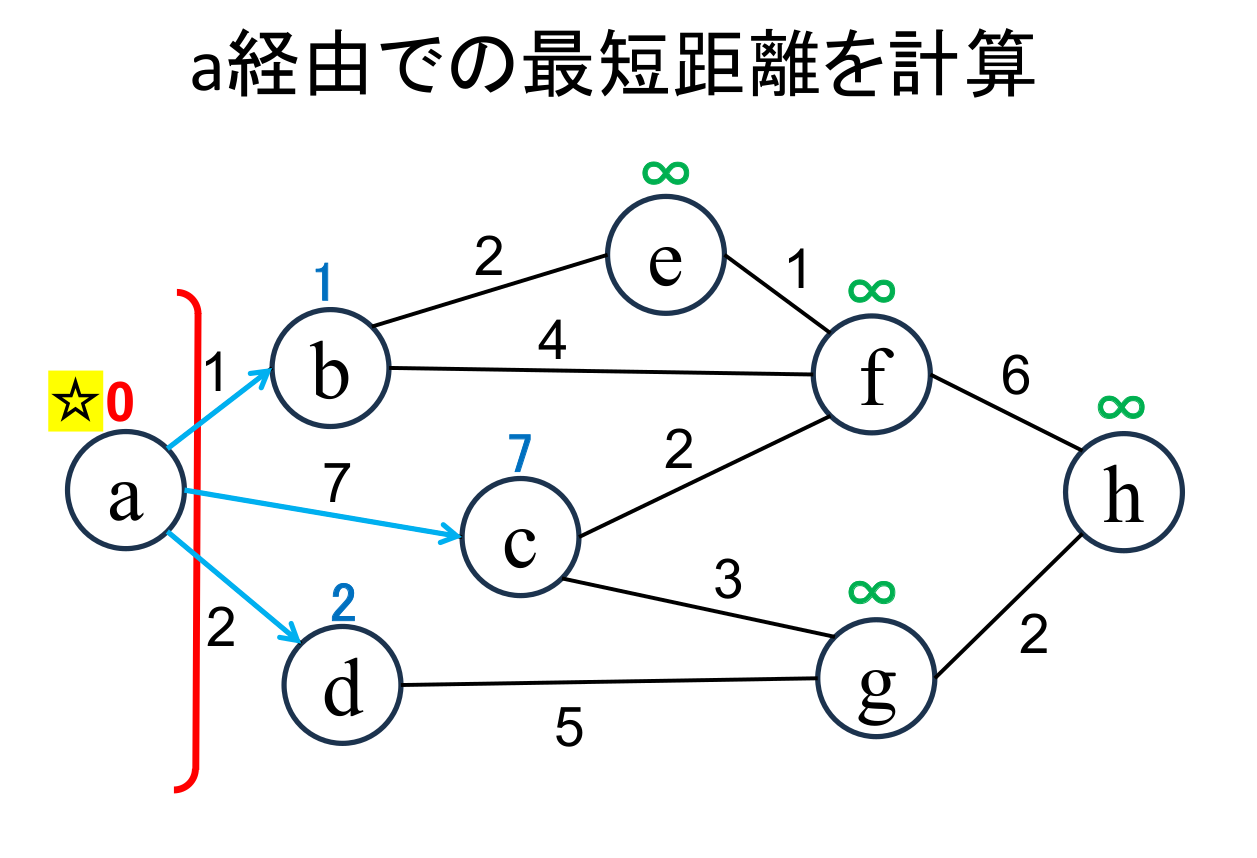 |
直近で確定した地点(☆印 がついている地点, a)から 「直接つながっている」かつ「未確定の」地点(b, c, d)に関して、 今確定した地点(a)を経由した場合の距離を 計算し、今までの距離よりも小さければ更新します。 (b,c,d がそれぞれ $\infty$から1,7,2に書き替りました)。 境界線を超えて未確定ノードの最短距離を書き換えたエッジを水色の矢印で表しています。 |
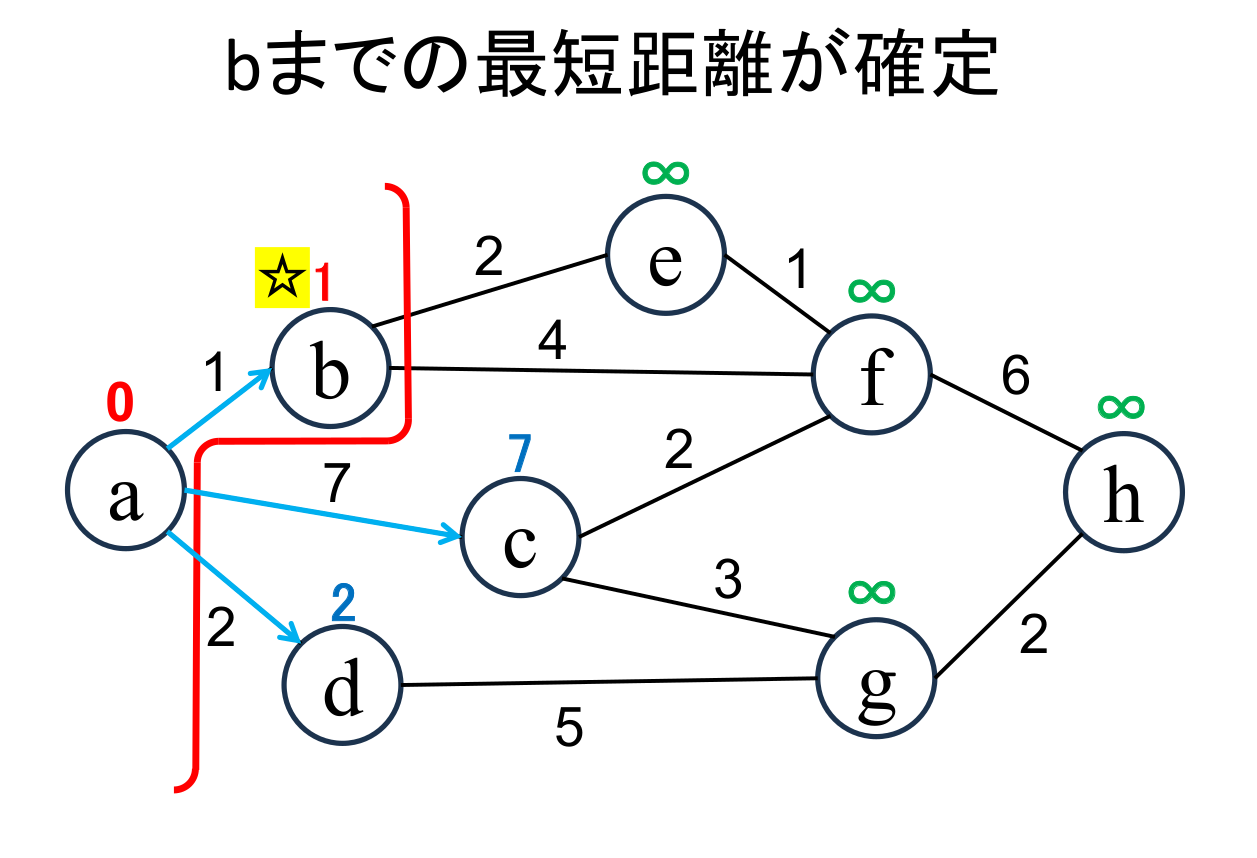 |
未確定の中から距離が最も小さい地点(b)を選んで、その距離 (1)を その地点の最小距離として確定します。 もし、最小値を持つ地点が複数ある場合は、そのなかのどれを 選んでも構いません。 直近で確定した地点(b)を☆印 をつけて表しています。 |
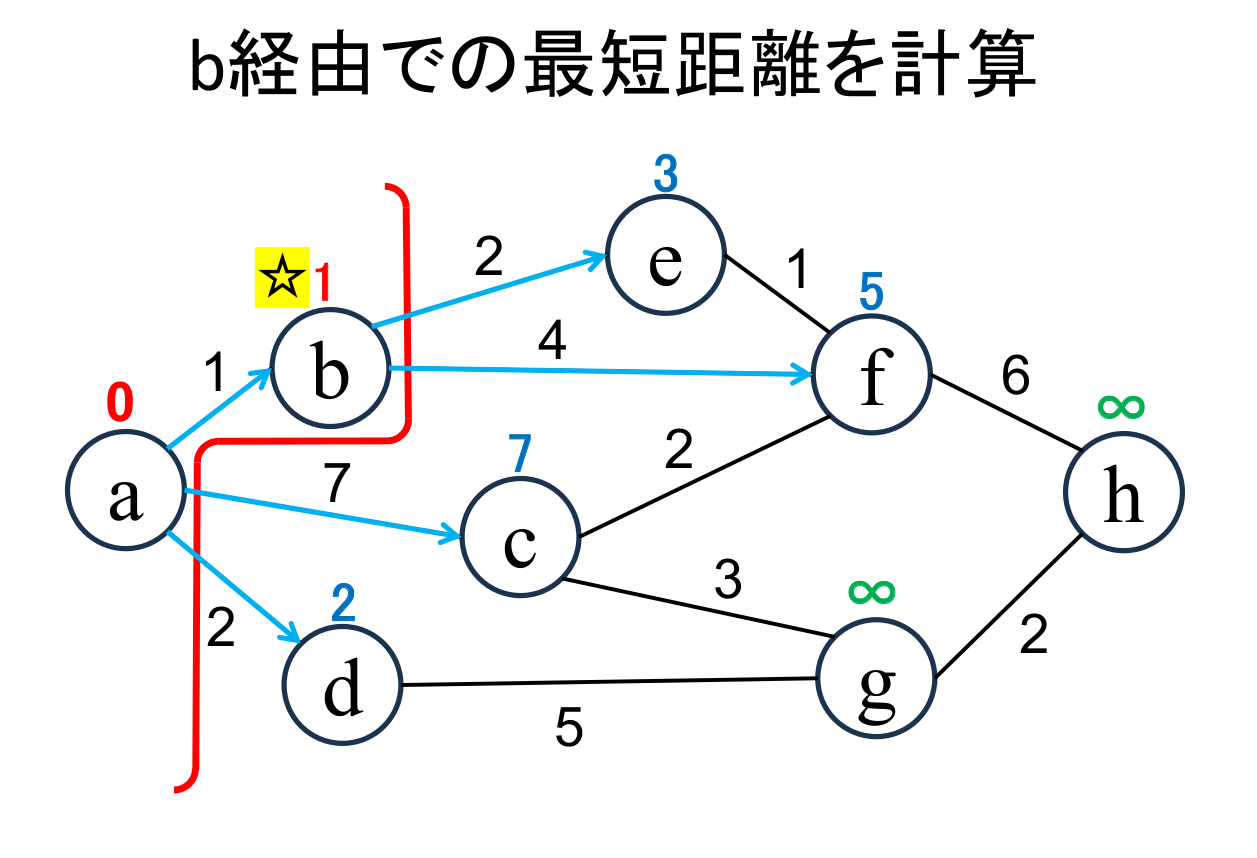 |
直近で確定した地点(☆印 がついている地点, b)から「直接つながっている」 かつ「未確定の」地点(e, f)に関して、今確定した地点(b)を経由した場合の距離を 計算し、今までの距離よりも小さければ更新します。 (e,fがそれぞれ3,5に書き替りました)。 |
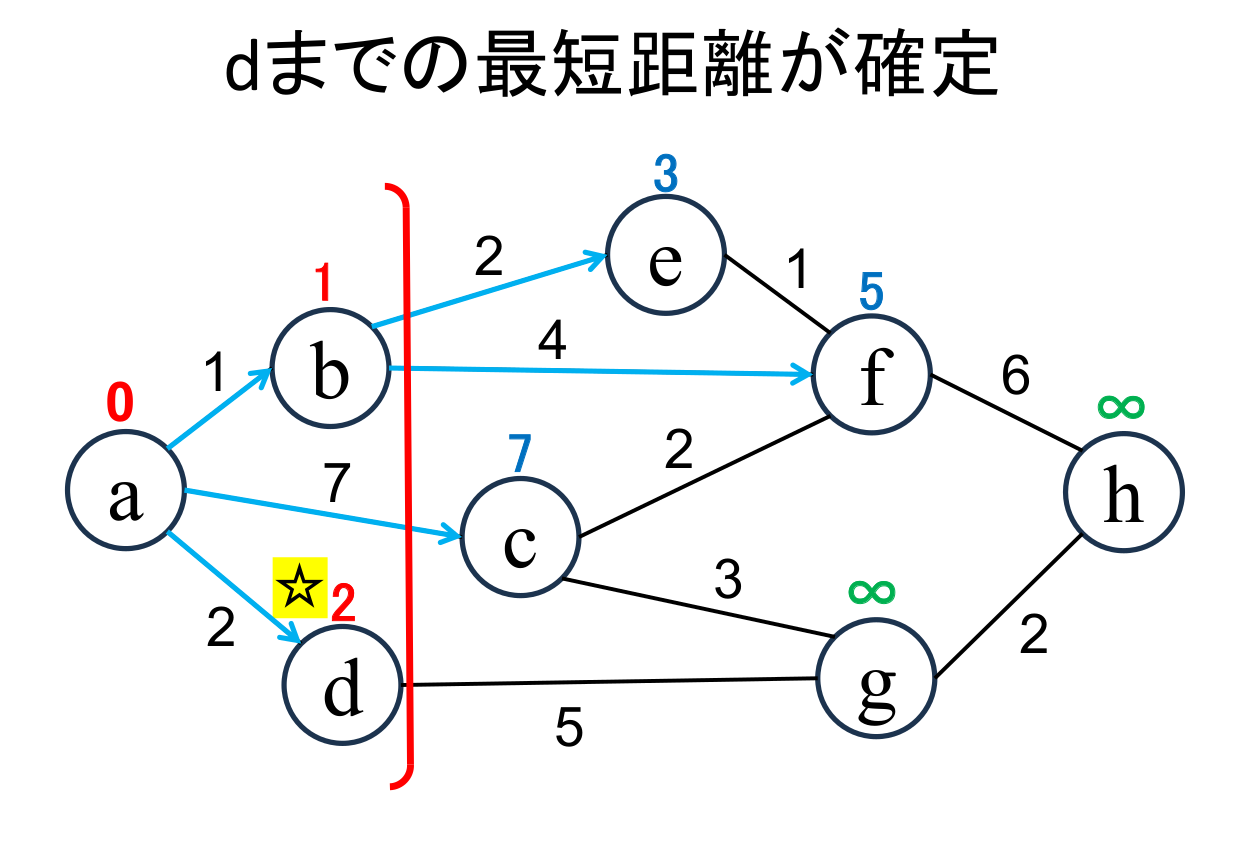 |
未確定の中から距離が最も小さい地点(d)を選んで、その距離 (2)を その地点の最小距離として確定します。 |
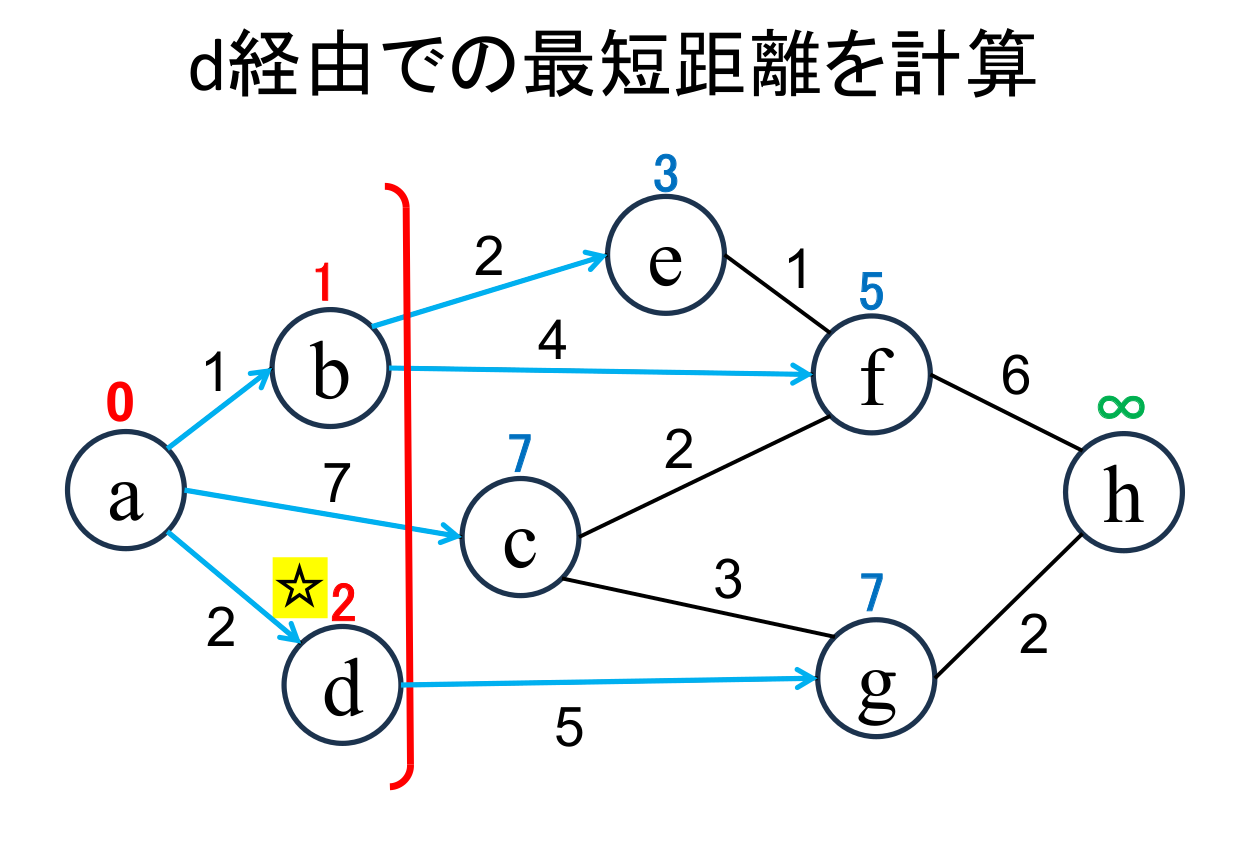 |
直近で確定した地点(☆印 がついている地点, d)から「直接つながっている」 かつ「未確定の」地点(g)に関して、今確定した地点を経由した場合の距離を計算し、 今までの距離よりも小さければ更新します。 (gが7に書き替りました)。 |
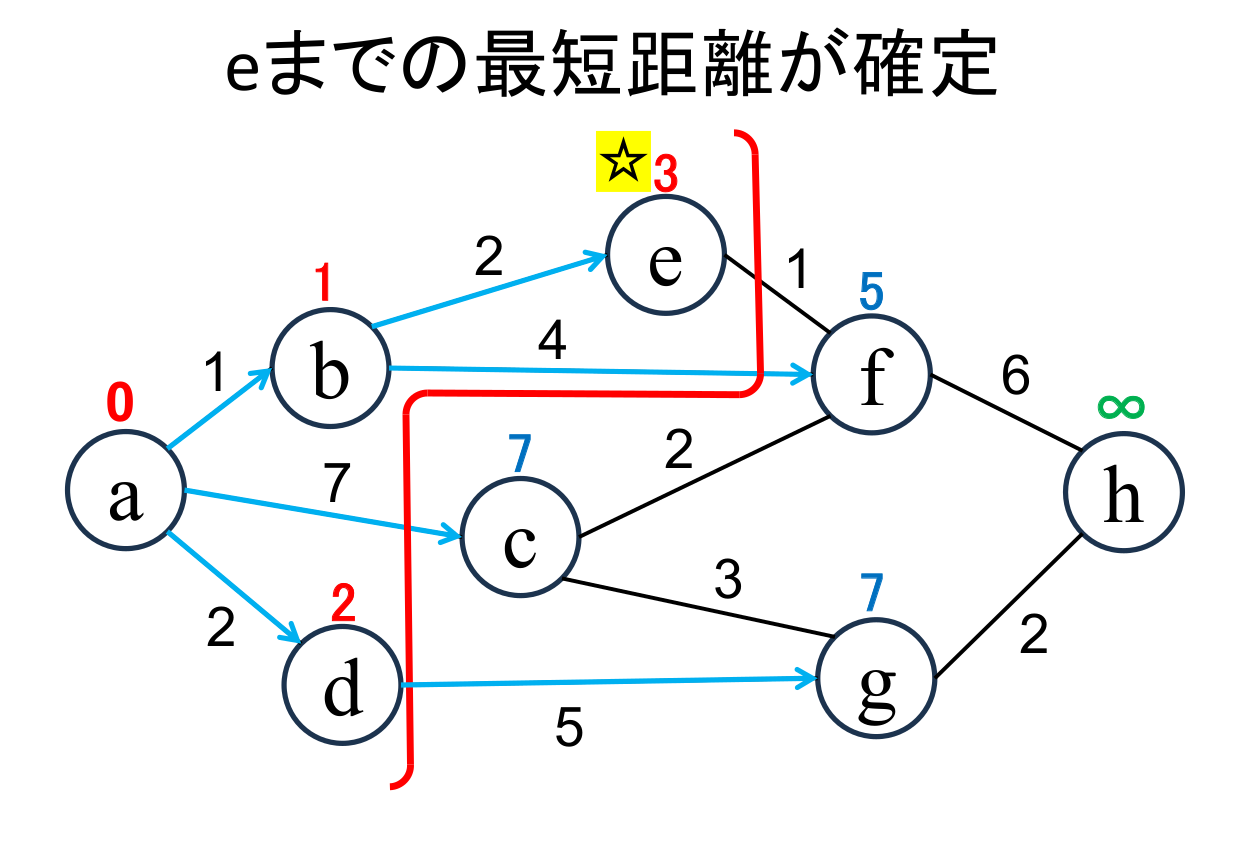 |
未確定の中から距離が最も小さい地点(e)を選んで、その距離 (3)を その地点の最小距離として確定します。 |
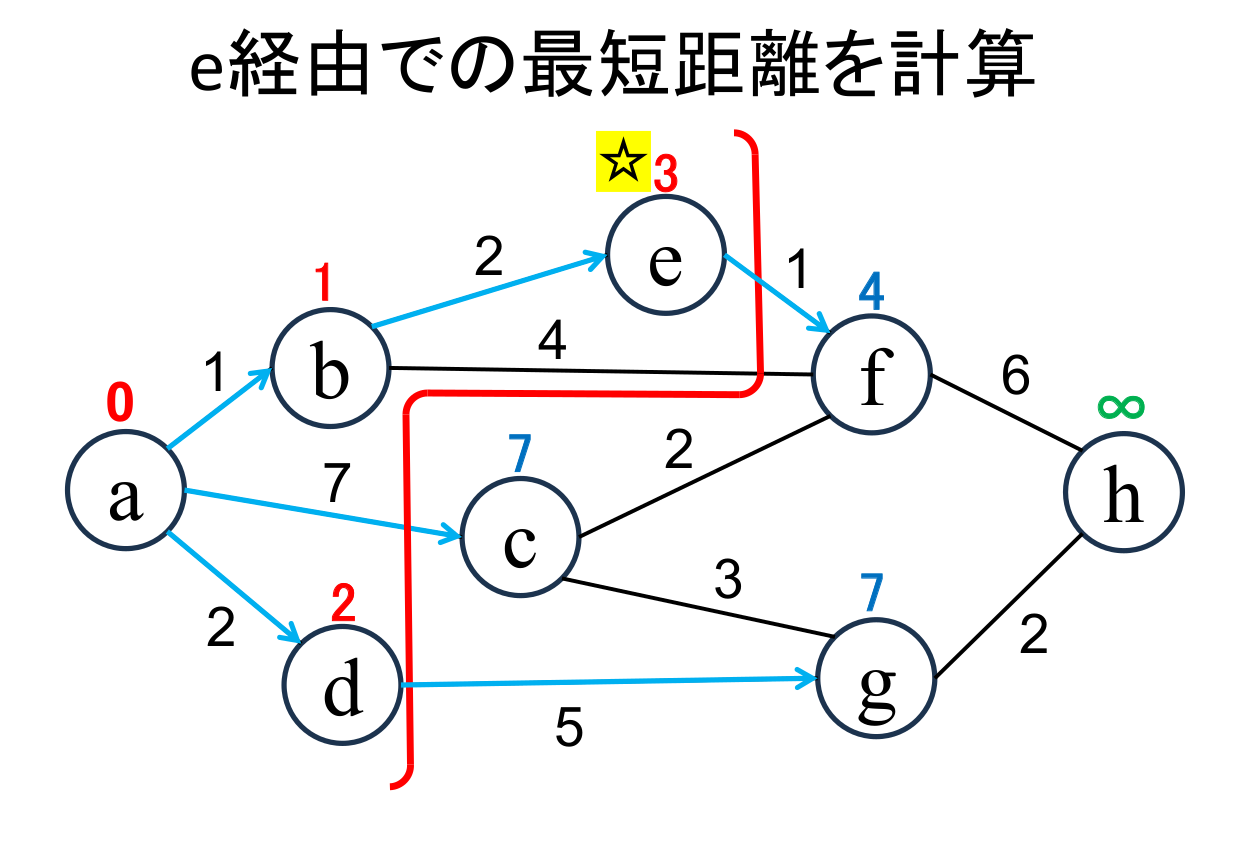 |
直近で確定した地点(☆印 がついている地点, e)から「直接つながっている」 かつ「未確定の」地点(f)に関して、今確定した地点を経由した場合の距離を計算し、 今までの距離よりも小さければ更新します。 (fが 4 に書き替りました)。 |
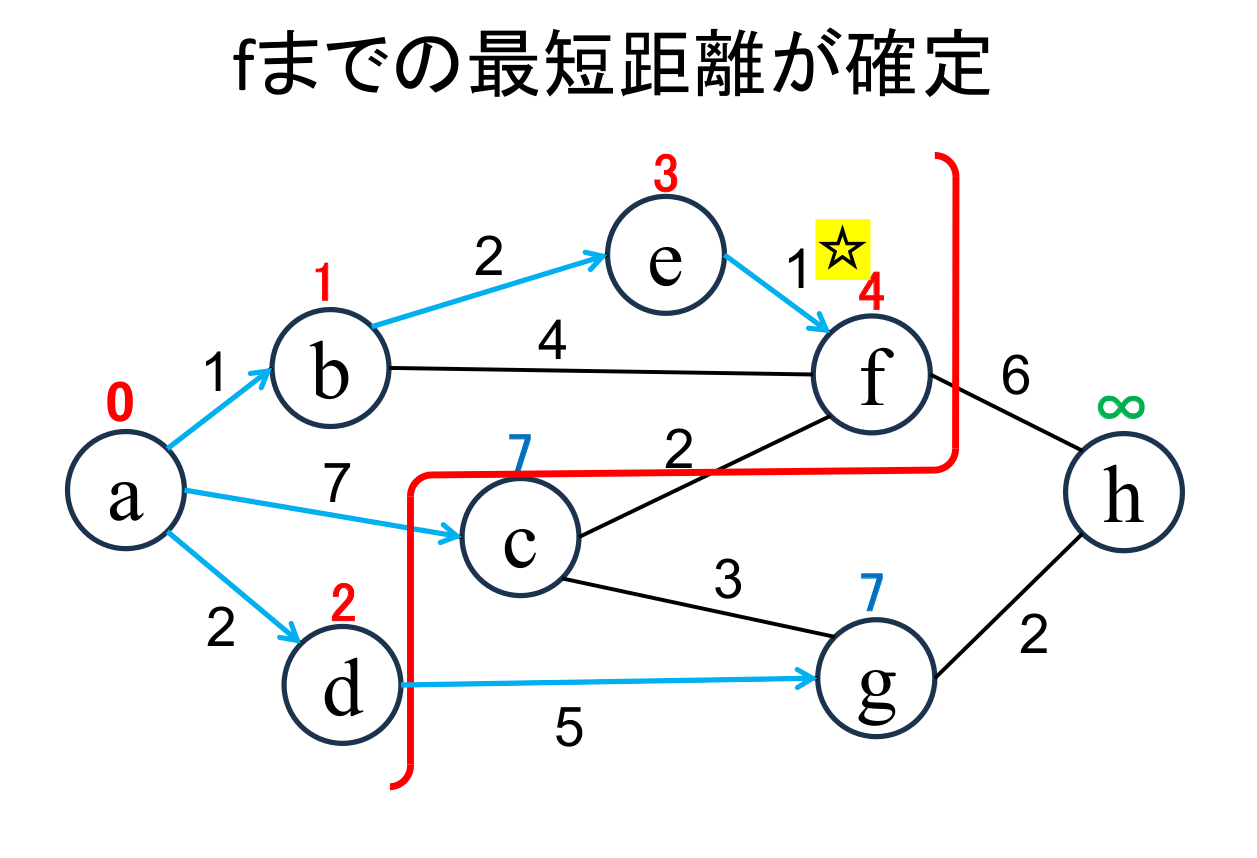 |
未確定の中から距離が最も小さい地点(f)を選んで、その距離 (4) を その地点の最小距離として確定します。 |
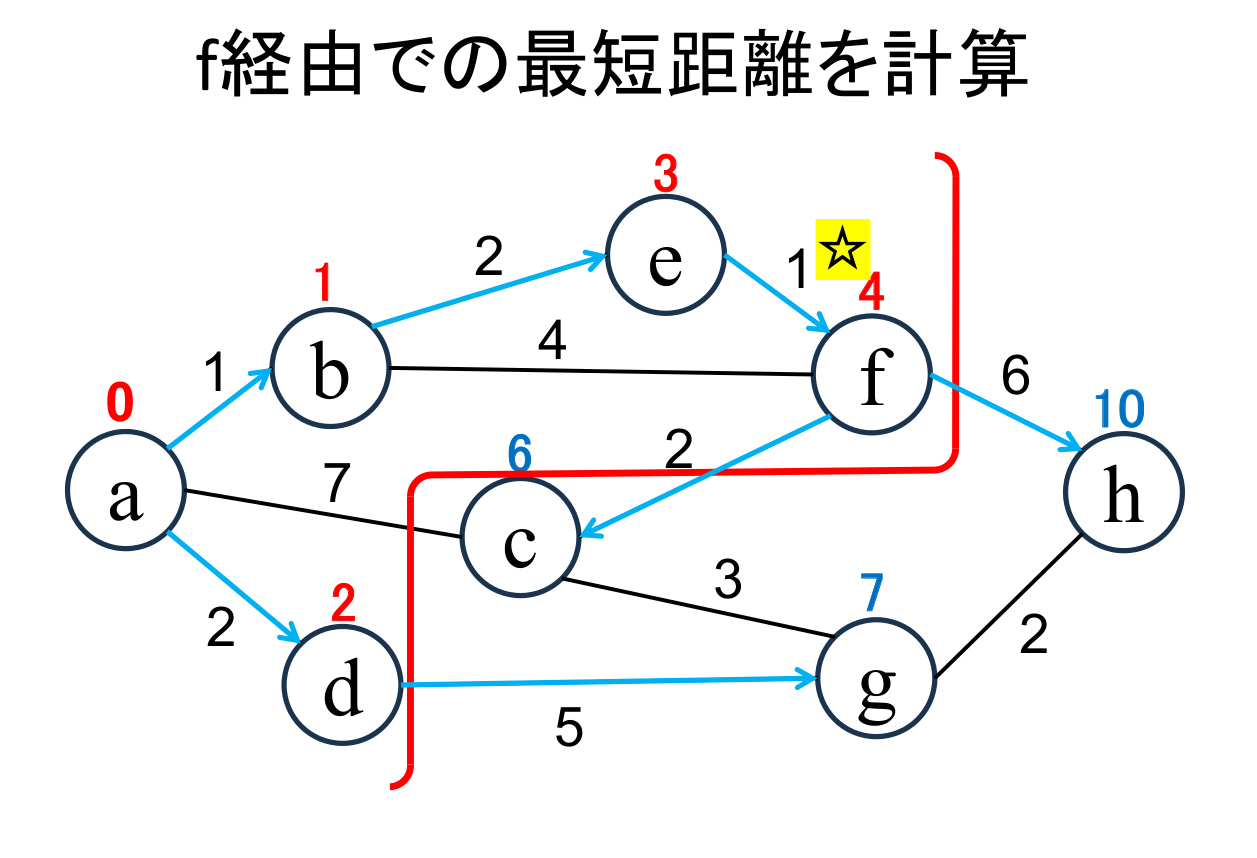 |
今確定した地点(☆印 がついている地点, f)から「直接つながっている」 かつ「未確定の」地点(c, h)に関して、今確定した地点を経由した場合の距離を計算し、 今までの距離よりも小さければ更新します。 (c,hがそれぞれ6,10に書き替りました)。 |
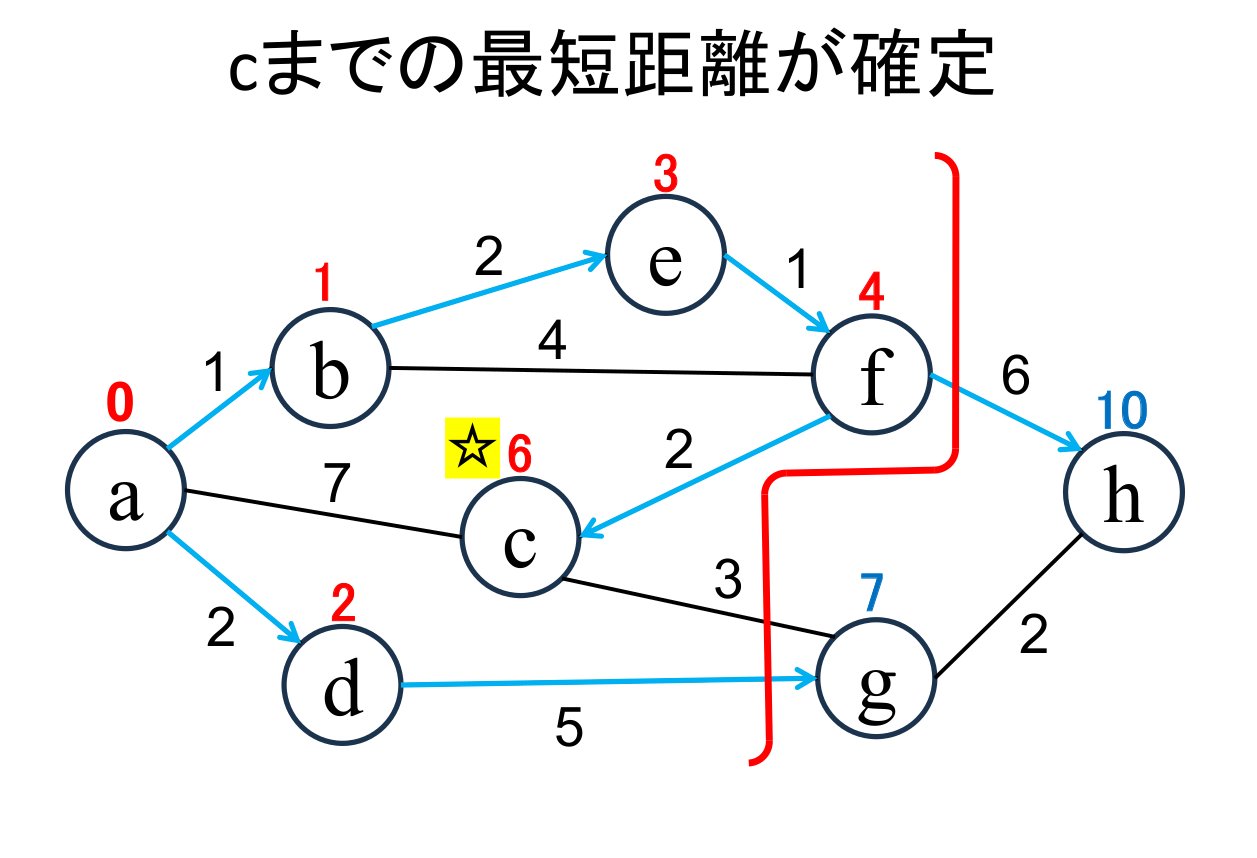 |
未確定の中から距離が最も小さい地点(c)を選んで、その距離 (6) を その地点の最小距離として確定します。 |
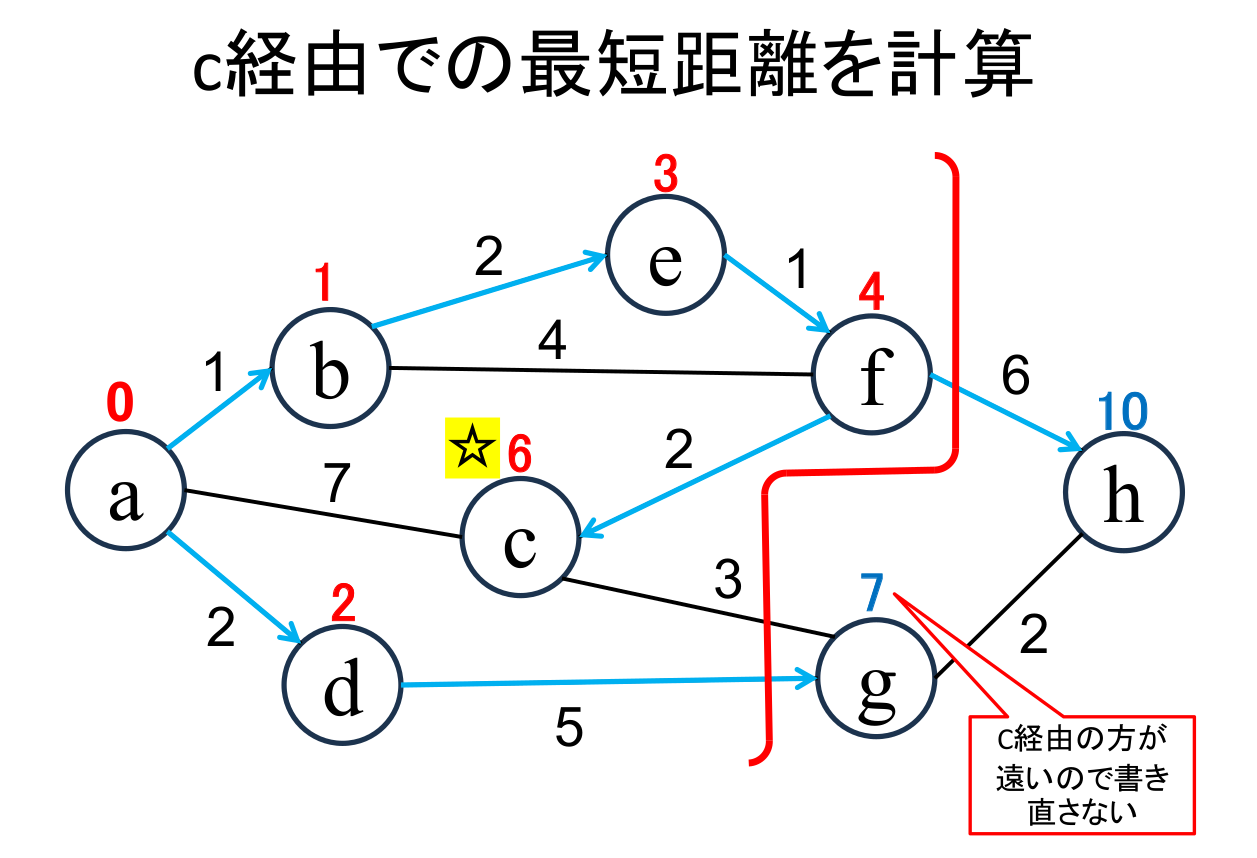 |
今確定した地点(☆印 がついている地点, c)から「直接つながっている」 かつ「未確定の」地点(g)に関して、今確定した地点を経由した場合の距離を計算し、 今までの距離よりも小さければ更新します。 (gは書き替りませんでした)。 |
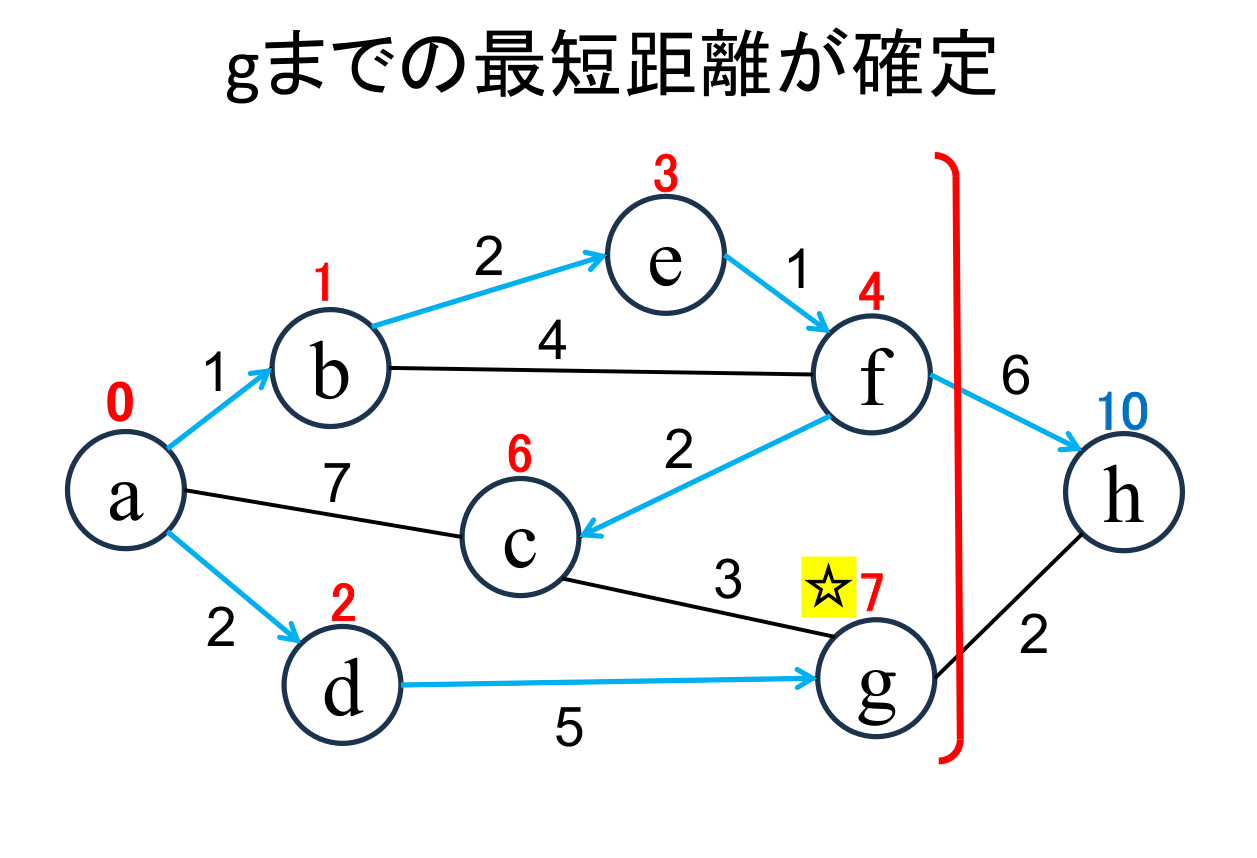 |
未確定の中から距離が最も小さい地点(g)を選んで、その距離 (7) を その地点の最小距離として確定します。 |
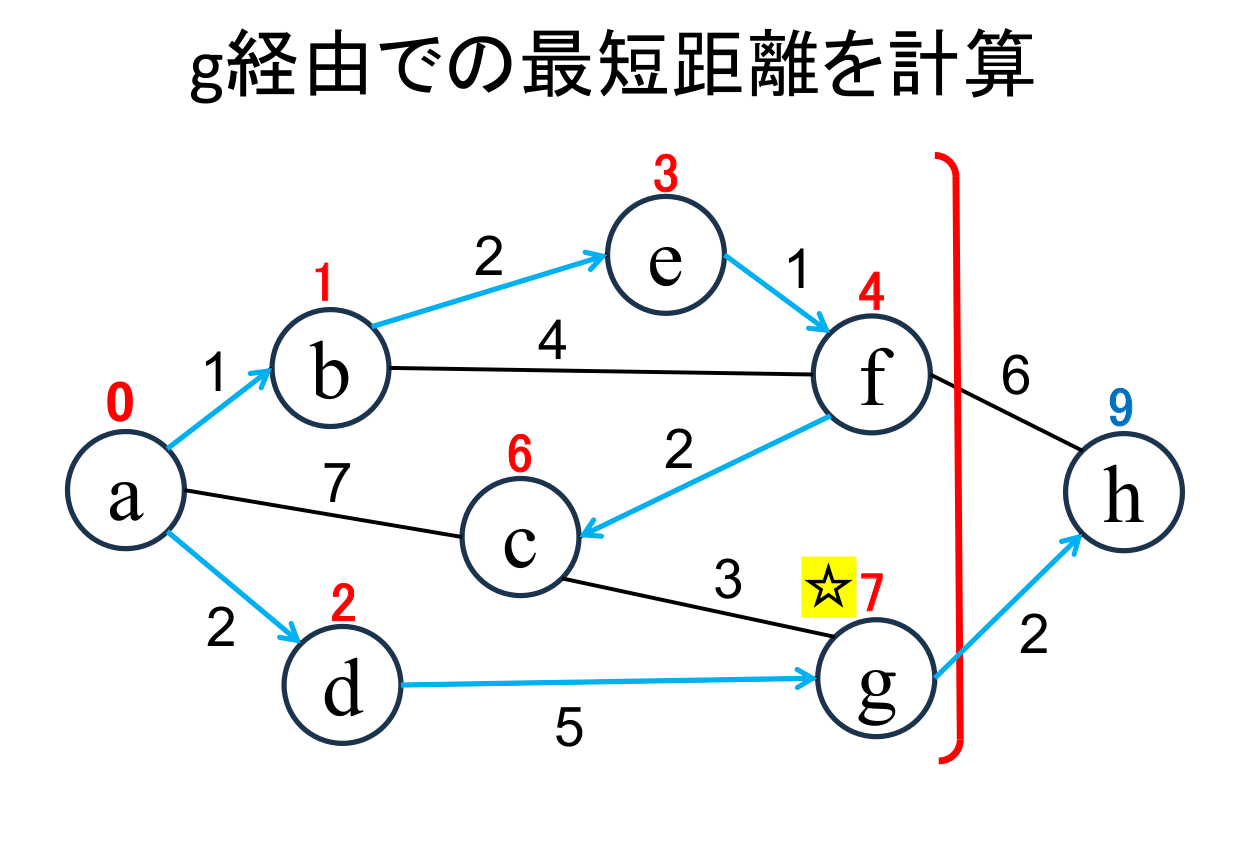 |
今確定した地点(☆印 がついている地点, g)から「直接つながっている」 かつ「未確定の」地点(h)に関して、今確定した地点を経由した場合の距離を計算し、 今までの距離よりも小さければ更新します。 (hは 9 に書き替りました)。 |
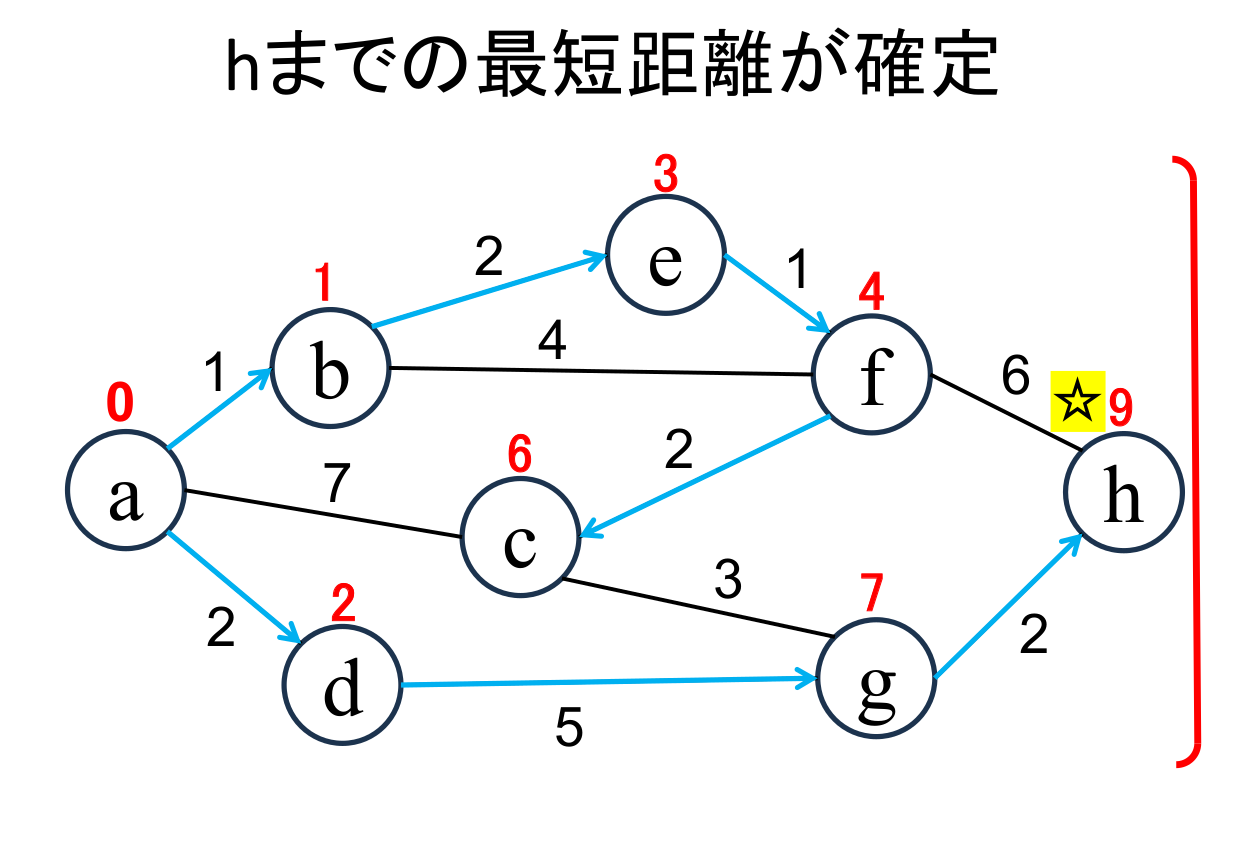 |
未確定の中から距離が最も小さい地点(h)を選んで、その距離 (9) を その地点の最小距離として確定します。 これで全ての地点までの最短距離が確定しました。 |
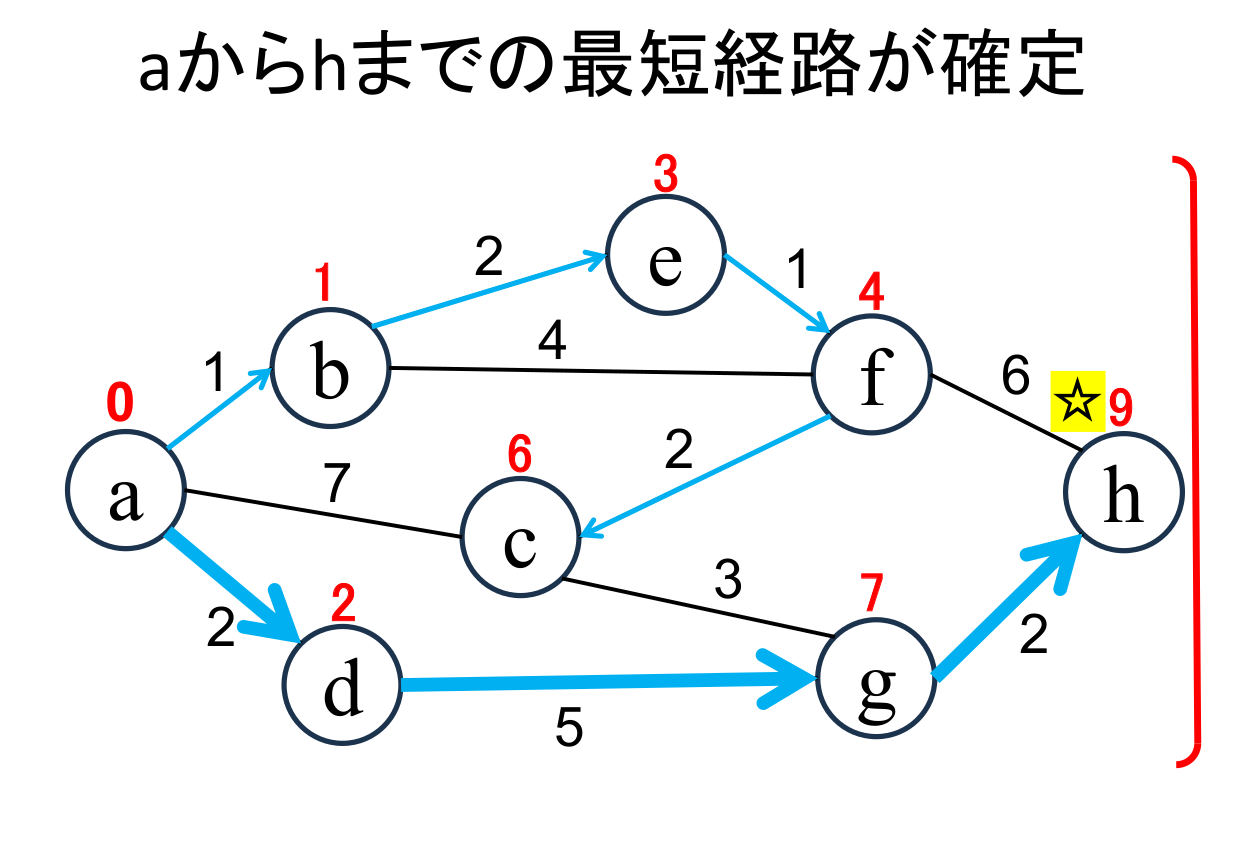 |
始点aから終点hまでの最短距離 (9)と最短経路(a → d → g → h )が確定します。 |
ダイクストラ法で、最短距離が正しく求まる理由を説明します。

上図は、「ノードb が確定し、ノードe, f への推定距離が更新」された直後で、
赤い境界線が確定ノード群と未確定ノード群を隔てていて、 境界線の左側が確定したノードで、右側が未確定なノードです。
この状況で、ダイクストラ法は 「未確定なノードのうちで最小のノード (d) への最短距離を現在の推定値 (2) で確定してよい」 ことを主張します。 そして、その主張が正しいことは 「ダイクストラ法が対象にしているグラフはエッジの重みが 0 以上」であることから明らかです。
境界線の右側にある未確定なノードを見ると、 「未確定だが推定値あり」なノード (c, d, e, f)は、 それぞれ現時点での 確定ノード(a, b)のどれかを経由した最短距離(推定値)を保持しています。 これらの中で最小の値を持つノード (d) は、「未確定かつ無限大」 なノード(g, h) たちを含めても最小となります。 このため、ノード d に対して他の未確定ノードを経由すると必ず遠回り(現在の値よりも大きな距離)になってしまいます。 なにしろ全てのエッジの重みは0以上ですから。
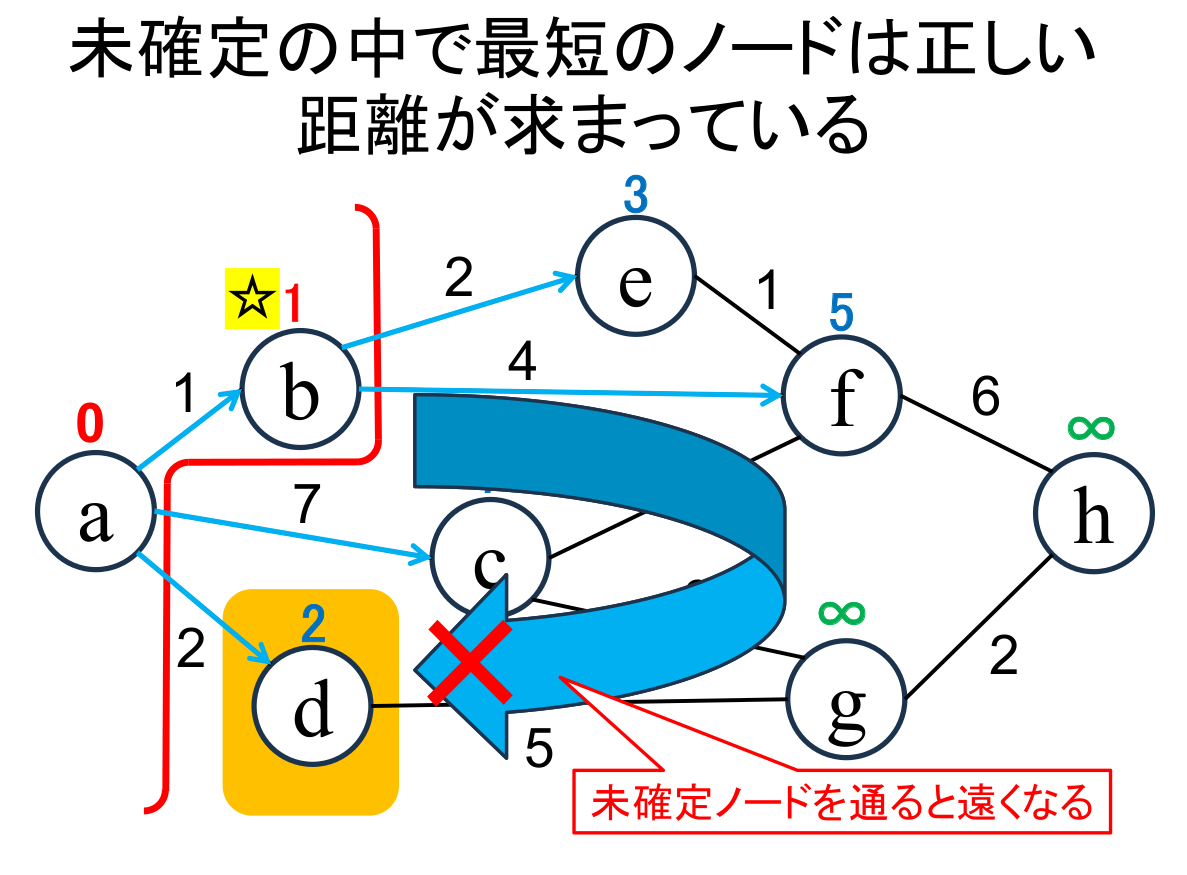
つまり、始点からノード d への最短距離は現時点で正しく推定されており、 現在の値で確定してよいのです。

このように考えると、ダイクストラ法はごくごく当たり前のことを主張していることがわかります。
「確定ノード群」と「未確定ノード群」を隔てる境界線に着目すると理解しやすくなります。 境界線に接している未確定ノード群のうちで現在最小のノードは「他の未確定ノードを経由してさらに小さくなりようがない」、 すなわち、「既に最小値が求まっている」ことが容易に納得できると思います。
一回のループでひとつの地点の最短距離が確定します。 これを $n$ 個の地点に関して繰り返しますので、この繰り返し操作の計算量は $O(n)$ です。
ひとつの地点の最短距離が確定したら、その地点とつながっている各地点の推定距離を更新します。 あるノードにつながっているノードは数は最大で $n-1$ 個ありますので、この操作の計算量は$O(n)$です。
したがって、全体の計算量は $O(n) \times O(n) = O(n^2)$ となります。
次のグラフに関して、出発地点をa, 目的地点をiとしたときの、 最短経路の距離を答えなさい。
a: 出発ノード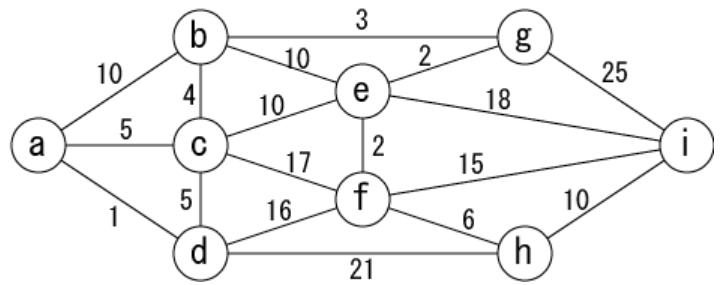
dijkstraPath.py を次のデータに対して動作させて、計算時間を計測して下さい。
| dijkstra.py |
#!/usr/bin/env python
import queue
G = [{}]
def setNode(n):
global G
G = [{} for i in range(n)]
def addEdge(s,t,w):
global G
G[s][t]=w
def solve(s,t):
global G
fixed = {}
q = queue.PriorityQueue()
q.put((0,s))
while q.empty() == False:
w,x = q.get()
if x in fixed: continue;
fixed[x] = w
if x == t: return w
for y in G[x]:
if (y in fixed) == False:
q.put((w + G[x][y], y))
return None
n,m = map(int,input().split())
setNode(n)
for i in range(m):
s,t,w = map(int,input().split())
addEdge(s,t,w)
addEdge(t,s,w)
src, dst = map(int,input().split())
print(solve(src,dst))
|
| dijkstra.pyの実行例 |
$ ./dijkstra.py < route03.data |
ノードへの距離を更新するときに、直前に経由したノードを via[] に記録しておきます。 目的地ノードまでの最短距離が決定したら、経由ノードを逆順にたどれば最短経路が求まります。
| dijkstraPath.py |
#!/usr/bin/env python
import queue
G = [{}]
def setNode(n):
global G
G = [{} for i in range(n)]
def addEdge(s,t,w):
global G
G[s][t]=w
def getRoute(via,s,t):
r = [t]
y = t
while y != s:
y = via[y]
r.append(y)
r.reverse()
return r
def solve(s,t):
global G
fixed = {}
via = {}
q = queue.PriorityQueue()
q.put((0,s,None))
while q.empty() == False:
w,x,prev = q.get()
if x in fixed: continue;
fixed[x] = w
via[x] = prev
if x == t:
return w, getRoute(via,s,t)
for y in G[x]:
if (y in fixed) == False:
q.put((w + G[x][y],y,x))
return None, None
n,m = map(int,input().split())
setNode(n)
for i in range(m):
s,t,w = map(int,input().split())
addEdge(s,t,w)
addEdge(t,s,w)
src, dst = map(int,input().split())
d,r = solve(src,dst)
print(d)
print(r)
|
| dijkstraPath.pyの実行例 |
$ ./dijkstraPath.py < route03.data |
Java で、敢えて愚直に書いた遅いプログラムは次のようになります。
| Dijkstra.java |
import java.util.*;
public class Dijkstra {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in); // 標準入力から読む
int n = sc.nextInt(); // ノードの数
int m = sc.nextInt(); // エッジの数
int[][] mat = new int[n][n]; // ノードの接続関係を表す隣接行列
for (int i=0; i<n; i++) // 隣接行列を初期化する
for (int j=0; j<n; j++)
mat[i][j] = (i==j) ? 0 : -1;
for (int i=0; i<m; i++) { // エッジの定義を読み込む
int s = sc.nextInt(); // 始点
int t = sc.nextInt(); // 終点
int w = sc.nextInt(); // 重み
mat[s][t] = mat[t][s] = w;
}
int src = sc.nextInt(); // スタートノード
int dst = sc.nextInt(); // 目的地ノード
int d = dijkstra(mat,src,dst);
System.out.println((d==Integer.MAX_VALUE) ? "no route" : d);
}
public static int dijkstra(int[][] mat,int src,int dst) {
int n = mat.length;
int[] distance = new int[n]; // 各ノードへの最短距離
boolean[] fixed = new boolean[n]; // 各ノードの最短距離が確定したか?
for (int i=0; i<n; i++) { // ノードを初期化する
distance[i] = Integer.MAX_VALUE; // 距離は無限大
fixed[i] = false; // 最短距離は未確定
}
distance[src] = 0; // 始点ノードの距離は0
while (true) {
int x = minIndex(distance,fixed); // 未確定の中で最小のノード
if (x == dst) return distance[x]; // 解を発見した
if (x < 0 || distance[x]==Integer.MAX_VALUE) return Integer.MAX_VALUE; // 非連結グラフ
fixed[x] = true; // ノード x までの距離は確定となる
for (int y=0; y<n; y++) { // 各ノードに関して
if (mat[x][y]>0 && !fixed[y]) { // xからyへエッジが存在し、yが未確定ならば
int d2 = distance[x]+mat[x][y];// xを経由したyまでの距離
// 今までの距離よりも小さければ、それを覚える
if (d2 < distance[y]) distance[y] = d2;
}
}
}
}
// fixed[]がfalseの中で、distance[]が最小のインデックスを返す
static int minIndex(int[] distance,boolean[] fixed) {
int idx = -1;
for (int i=0; i<fixed.length; i++) {
if (!fixed[i]) // 未確定で
if (idx < 0 || distance[idx] > distance[i]) idx = i; // 最小距離のインデックス
}
return idx;
}
}
|
| Dijkstra.javaの実行例 |
$ javac Dijkstra.java |
Dijkstra.java はグラフの接続関係を2次元配列としてメモリに保持するので、 ノード数が大きいデータを入力として与えると実行環境によっては 「ヒープメモリが確保できない」というエラー(例外)を起こして プログラムの実行が途中で終了することがあります。 その場合は、javaコマンドの-Xmsオプションでjava仮想マシンのヒープメモリを広げて 実行します。
| route13.data(一部) |
62500 124906 0 1 15 0 250 58 1 2 79 1 251 1 2 3 144 ...(略)... |
| ヒープメモリを広げて Dijkstra.java を実行する例 |
$ javac Dijkstra.java |
最短経路を表示するように変更してみましょう。
各地点の距離を更新するときに、どの地点を直前に経由したのかを 記録するようにします。
DijkstraPath.javaの変更点diff -c Dijkstra.java DijkstraPath.javaの出力 |
*** Dijkstra.java Mon Jun 19 13:40:15 2023
--- DijkstraPath.java Mon Jun 19 13:40:28 2023
***************
*** 1,3 ****
import java.util.*;
! public class Dijkstra {
public static void main(String[] args) {
--- 1,4 ----
import java.util.*;
! public class DijkstraPath {
! static int[] via; // 経由ノード
public static void main(String[] args) {
***************
*** 19,21 ****
int d = dijkstra(mat,src,dst);
! System.out.println((d==Integer.MAX_VALUE) ? "no route" : d);
}
--- 20,40 ----
int d = dijkstra(mat,src,dst);
! if (d == Integer.MAX_VALUE) {
! System.out.println("no route");
! } else {
! System.out.println(d);
! StringBuilder sb = new StringBuilder();
! for (int x: getRoute(src, dst)) sb.append(x + " ");
! System.out.println(sb.toString());
! }
! }
! static ArrayList<Integer> getRoute(int src, int dst) {
! ArrayList<Integer> r = new ArrayList<>();
! r.add(dst);
! int x = dst;
! while (x != src) {
! x = via[x];
! r.add(x);
! }
! Collections.reverse(r);
! return r;
}
***************
*** 25,26 ****
--- 44,46 ----
boolean[] fixed = new boolean[n]; // 各ノードの最短距離が確定したか?
+ via = new int[n]; // 経由ノード
for (int i=0; i<n; i++) { // ノードを初期化する
***************
*** 28,29 ****
--- 48,50 ----
fixed[i] = false; // 最短距離は未確定
+ via[i] = -1; // 経由ノードは未確定
}
***************
*** 39,41 ****
// 今までの距離よりも小さければ、それを覚える
! if (d2 < distance[y]) distance[y] = d2;
}
--- 60,62 ----
// 今までの距離よりも小さければ、それを覚える
! if (d2 < distance[y]) { distance[y] = d2; via[y] = x; }
}
|
| DijkstraPath.javaの実行例 |
$ javac DijkstraPath.java |
ノードの数が多い疎なグラフを表すデータ、たとえば route13.data に対しては、DijkstraPath.java をヒープを広げて実行してみましょう。 実行環境によっては、時間はかかりますが計算できます。
| route13.data に対する DijkstraPath.java の実行時間 CPU:Ryzen 5900HX, Memory: DDR4 32GB |
$ time (java -Xms16g DijkstraPath < route13.data >/dev/null) |
ダイクストラ法において、疎なグラフ(つまりノード数に比べて エッジの数が少ないグラフ)を扱う場合には、
Priority First Search の計算量は、
「$n$個の各ノードについて」$\times$ (「ヒープから最小のノードを取り出す手間」 + 「新規確定ノードにつながるノードの推定値を再計算する手間」)
となります。ここで、
「ヒープから最小のノードを取り出す手間」: $\log n$
「新規確定ノードにつながるノードの推定値を再計算する手間」: $n$ ← 疎なグラフなので定数とみなせる
なので、実際の計算は
$O(n) \times O( \log n + \mbox{定数}) = O(n \log n)$
で行われることが期待できる、というわけです。
Priority Queueは「ヒープ」と呼ばれる、 「特定のデータへのアクセスが$O(\log n)$で可能」 なデータ構造です。
JavaではPriorityQueueクラスが標準ライブラリにありますので、 これを使ってPriority First Searchを記述してみましょう。
| PFSPath.java |
import java.util.*;
public class PFSPath {
static ArrayList<Node> graph = new ArrayList<>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in); // 標準入力から読む
int n = sc.nextInt(); // ノードの数
int m = sc.nextInt(); // エッジの数
for (int i=0; i<n; i++)
graph.add(new Node(i, Integer.MAX_VALUE)); // 各ノードを生成する
for (int i=0; i<m; i++) { // エッジの定義を読み込む
int s = sc.nextInt(); // 始点
int t = sc.nextInt(); // 終点
int w = sc.nextInt(); // 重み
graph.get(s).addEdge(t,w); // ノードsからtにエッジを張る
graph.get(t).addEdge(s,w); // ノードtからsにエッジを張る
}
Node src = graph.get(sc.nextInt()); // スタートノード
Node dst = graph.get(sc.nextInt()); // 目的地ノード
int d = dijkstra(src, dst);
if (d ==Integer.MAX_VALUE) {
System.out.println("no route");
} else {
System.out.println(d);
StringBuilder sb = new StringBuilder();
for (Node x: getRoute(src, dst)) sb.append(x.id + " ");
System.out.println(sb.toString());
}
}
public static int dijkstra(Node src, Node dst) {
HashSet<Node> fixed = new HashSet<>(); // 最短距離が確定したノード
src.d = 0; // 始点ノードの距離を0とおく
var queue = new PriorityQueue<Node>();
queue.add(src);
while (queue.size() > 0) {
Node x = queue.poll(); // キューからの中で最小のノードを取り出す
assert !fixed.contains(x);
if (x == dst) return x.d; // 解を発見した
fixed.add(x); // x を確定ノードとする
for (Map.Entry<Integer,Integer> entry: x.edges.entrySet()) { // xから出ている各エッジに対して
Node y = graph.get(entry.getKey()); // エッジの終端ノード
int w = entry.getValue(); // エッジの重み
int d2 = x.d + w; // xを経由したyまでの距離
if (fixed.contains(y) || d2 >= y.d) continue; // 「すでに確定済み」or「x経由は遠い」場合何もしない
if (queue.contains(y)) queue.remove(y); // yがキューに含まれる場合は一旦取り出す
y.d = d2; // yまでの距離を更新して
y.via = x; // yの経由地はx
queue.add(y); // yをキューに追加する
}
}
return Integer.MAX_VALUE; // 到達不可能(非連結グラフ)
}
static ArrayList<Node> getRoute(Node src, Node dst) { // src->dst の最短経路
ArrayList<Node> r = new ArrayList<>();
r.add(dst); // dst から始めて
Node x = dst;
while (x != src) { //src まで逆順にたどる
x = x.via;
r.add(x);
}
Collections.reverse(r); // src->dst の順に並べ直す
return r;
}
static class Node implements Comparable<Node> { // ノードの定義 (比較可能)
int id; // ノード番号
int d; // 距離
Node via; // 直前の経由ノード
HashMap<Integer, Integer> edges; // エッジ: toノード, 重み
public Node(int id, int d) {
this.id = id;
this.d = d;
edges = new HashMap<>();
}
void addEdge(int t, int w) { edges.put(t, w); }
public int compareTo(Node x) { return d - x.d; }
}
}
|
| PFSPath.java の実行例 |
$ java PFSPath < route03.data |
ノードの数が多い疎なグラフを表すデータ、たとえば route13.data に対して、PFSPath.java を実行してみましょう。 DijkstraPath.java の場合とは異なり、「小さなメモリ消費量」で且つ「高速」に答が得られることがわかります。
| route13.data に対する PFSPath.java の実行時間 CPU:Ryzen 5900HX, Memory: DDR4 32GB |
$ time (java PFSPath < route13.data >/dev/null) |