1. Introduction

This document describes PTX, a low-level parallel thread execution virtual machine and instruction set architecture (ISA). PTX exposes the GPU as a data-parallel computing device.

1.1. Scalable Data-Parallel Computing using GPUs

Driven by the insatiable market demand for real-time, high-definition 3D graphics, the programmable GPU has evolved into a highly parallel, multithreaded, many-core processor with tremendous computational horsepower and very high memory bandwidth. The GPU is especially well-suited to address problems that can be expressed as data-parallel computations - the same program is executed on many data elements in parallel - with high arithmetic intensity - the ratio of arithmetic operations to memory operations. Because the same program is executed for each data element, there is a lower requirement for sophisticated flow control; and because it is executed on many data elements and has high arithmetic intensity, the memory access latency can be hidden with calculations instead of big data caches.

Data-parallel processing maps data elements to parallel processing threads. Many applications that process large data sets can use a data-parallel programming model to speed up the computations. In 3D rendering large sets of pixels and vertices are mapped to parallel threads. Similarly, image and media processing applications such as post-processing of rendered images, video encoding and decoding, image scaling, stereo vision, and pattern recognition can map image blocks and pixels to parallel processing threads. In fact, many algorithms outside the field of image rendering and processing are accelerated by data-parallel processing, from general signal processing or physics simulation to computational finance or computational biology.

PTX defines a virtual machine and ISA for general purpose parallel thread execution. PTX programs are translated at install time to the target hardware instruction set. The PTX-to-GPU translator and driver enable NVIDIA GPUs to be used as programmable parallel computers.

1.2. Goals of PTX

PTX provides a stable programming model and instruction set for general purpose parallel programming. It is designed to be efficient on NVIDIA GPUs supporting the computation features defined by the NVIDIA Tesla architecture. High level language compilers for languages such as CUDA and C/C++ generate PTX instructions, which are optimized for and translated to native target-architecture instructions.

The goals for PTX include the following:
  • Provide a stable ISA that spans multiple GPU generations.
  • Achieve performance in compiled applications comparable to native GPU performance.
  • Provide a machine-independent ISA for C/C++ and other compilers to target.
  • Provide a code distribution ISA for application and middleware developers.
  • Provide a common source-level ISA for optimizing code generators and translators, which map PTX to specific target machines.
  • Facilitate hand-coding of libraries, performance kernels, and architecture tests.
  • Provide a scalable programming model that spans GPU sizes from a single unit to many parallel units.

1.3. PTX ISA Version 6.0

PTX ISA version 6.0 introduces the following new features:
  • Support for sm_70 target architecture.
  • Specifies the memory consistency model for programs running on sm_70 and later architectures.
  • Various extensions to memory instructions to specify memory synchronization semantics and scopes at which such synchronization can be observed.
  • New instruction wmma for matrix operations which allows loading matrices from memory, performing multiply-and-accumulate on them and storing result in memory.
  • Support for new barrier instruction.
  • Extends neg instruction to support .f16 and .f16x2 types.
  • A new instruction fns which allows finding n-th set bit in integer.
  • A new instruction bar.warp.sync which allows synchronizing threads in warp.
  • Extends vote and shfl instructions with .sync modifier which waits for specified threads before executing the vote and shfl operation respectively.
  • A new instruction match.sync which allows broadcasting and comparing a value across threads in warp.
  • A new instruction brx.idx which allows branching to a label indexed from list of potential targets.
  • Support for unsized array parameter for .func which can be used to implement variadic functions.
  • Support for .b16 integer type in dwarf-lines.
  • Support for taking address of device function return parameters using mov instruction.

1.4. Document Structure

The information in this document is organized into the following Chapters:

References

2. Programming Model

2.1. A Highly Multithreaded Coprocessor

The GPU is a compute device capable of executing a very large number of threads in parallel. It operates as a coprocessor to the main CPU, or host: In other words, data-parallel, compute-intensive portions of applications running on the host are off-loaded onto the device.

More precisely, a portion of an application that is executed many times, but independently on different data, can be isolated into a kernel function that is executed on the GPU as many different threads. To that effect, such a function is compiled to the PTX instruction set and the resulting kernel is translated at install time to the target GPU instruction set.

2.2. Thread Hierarchy

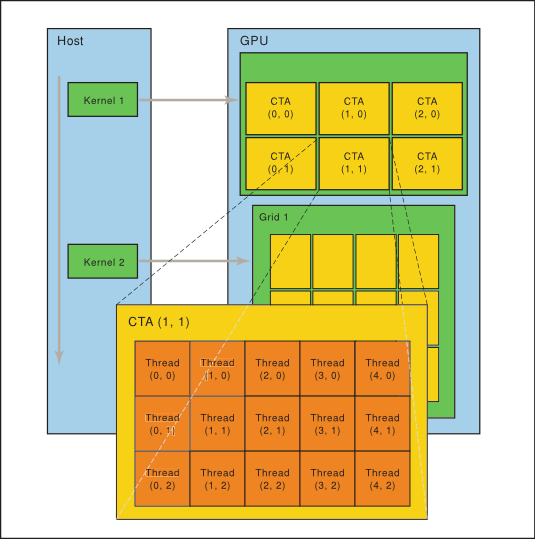
The batch of threads that executes a kernel is organized as a grid of cooperative thread arrays as described in this section and illustrated in Figure 1. Cooperative thread arrays (CTAs) implement CUDA thread blocks.

2.2.1. Cooperative Thread Arrays

The Parallel Thread Execution (PTX) programming model is explicitly parallel: a PTX program specifies the execution of a given thread of a parallel thread array. A cooperative thread array, or CTA, is an array of threads that execute a kernel concurrently or in parallel.

Threads within a CTA can communicate with each other. To coordinate the communication of the threads within the CTA, one can specify synchronization points where threads wait until all threads in the CTA have arrived.

Each thread has a unique thread identifier within the CTA. Programs use a data parallel decomposition to partition inputs, work, and results across the threads of the CTA. Each CTA thread uses its thread identifier to determine its assigned role, assign specific input and output positions, compute addresses, and select work to perform. The thread identifier is a three-element vector tid, (with elements tid.x, tid.y, and tid.z) that specifies the thread's position within a 1D, 2D, or 3D CTA. Each thread identifier component ranges from zero up to the number of thread ids in that CTA dimension.

Each CTA has a 1D, 2D, or 3D shape specified by a three-element vector ntid (with elements ntid.x, ntid.y, and ntid.z). The vector ntid specifies the number of threads in each CTA dimension.

Threads within a CTA execute in SIMT (single-instruction, multiple-thread) fashion in groups called warps. A warp is a maximal subset of threads from a single CTA, such that the threads execute the same instructions at the same time. Threads within a warp are sequentially numbered. The warp size is a machine-dependent constant. Typically, a warp has 32 threads. Some applications may be able to maximize performance with knowledge of the warp size, so PTX includes a run-time immediate constant, WARP_SZ, which may be used in any instruction where an immediate operand is allowed.

2.2.2. Grid of Cooperative Thread Arrays

There is a maximum number of threads that a CTA can contain. However, CTAs that execute the same kernel can be batched together into a grid of CTAs, so that the total number of threads that can be launched in a single kernel invocation is very large. This comes at the expense of reduced thread communication and synchronization, because threads in different CTAs cannot communicate and synchronize with each other.

Multiple CTAs may execute concurrently and in parallel, or sequentially, depending on the platform. Each CTA has a unique CTA identifier (ctaid) within a grid of CTAs. Each grid of CTAs has a 1D, 2D , or 3D shape specified by the parameter nctaid. Each grid also has a unique temporal grid identifier (gridid). Threads may read and use these values through predefined, read-only special registers %tid, %ntid, %ctaid, %nctaid, and %gridid.

The host issues a succession of kernel invocations to the device. Each kernel is executed as a batch of threads organized as a grid of CTAs (Figure 1).

Figure 1. Thread Batching

Thread Batching

Note: A cooperative thread array (CTA) is a set of concurrent threads that execute the same kernel program. A grid is a set of CTAs that execute independently.

2.3. Memory Hierarchy

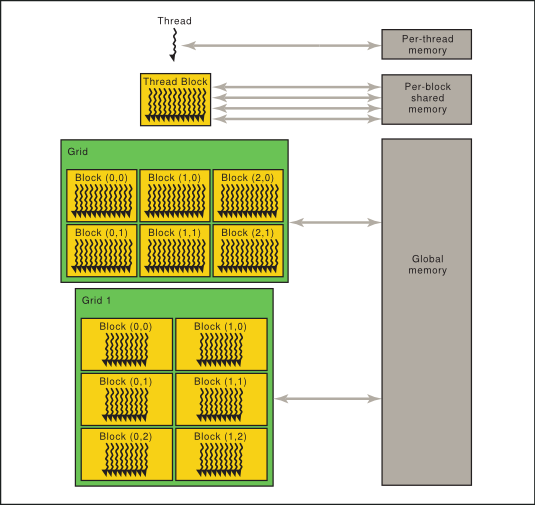
PTX threads may access data from multiple memory spaces during their execution as illustrated by Figure 2. Each thread has a private local memory. Each thread block (CTA) has a shared memory visible to all threads of the block and with the same lifetime as the block. Finally, all threads have access to the same global memory.

There are additional memory spaces accessible by all threads: the constant, texture, and surface memory spaces.  Constant and texture memory are read-only; surface memory is readable and writable. The global, constant, texture, and surface memory spaces are optimized for different memory usages. For example, texture memory offers different addressing modes as well as data filtering for specific data formats. Note that texture and surface memory is cached, and within the same kernel call, the cache is not kept coherent with respect to global memory writes and surface memory writes, so any texture fetch or surface read to an address that has been written to via a global or a surface write in the same kernel call returns undefined data. In other words, a thread can safely read some texture or surface memory location only if this memory location has been updated by a previous kernel call or memory copy, but not if it has been previously updated by the same thread or another thread from the same kernel call.

The global, constant, and texture memory spaces are persistent across kernel launches by the same application.

Both the host and the device maintain their own local memory, referred to as host memory and device memory, respectively. The device memory may be mapped and read or written by the host, or, for more efficient transfer, copied from the host memory through optimized API calls that utilize the device's high-performance Direct Memory Access (DMA) engine.

Figure 2. Memory Hierarchy

Memory Hierarchy

3. PTX Machine Model

3.1. A Set of SIMT Multiprocessors with On-chip Shared Memory

The NVIDIA Tesla architecture is built around a scalable array of multithreaded Streaming Multiprocessors (SMs). When a host program invokes a kernel grid, the blocks of the grid are enumerated and distributed to multiprocessors with available execution capacity. The threads of a thread block execute concurrently on one multiprocessor. As thread blocks terminate, new blocks are launched on the vacated multiprocessors.

A multiprocessor consists of multiple Scalar Processor (SP) cores, a multithreaded instruction unit, and on-chip shared memory. The multiprocessor creates, manages, and executes concurrent threads in hardware with zero scheduling overhead. It implements a single-instruction barrier synchronization. Fast barrier synchronization together with lightweight thread creation and zero-overhead thread scheduling efficiently support very fine-grained parallelism, allowing, for example, a low granularity decomposition of problems by assigning one thread to each data element (such as a pixel in an image, a voxel in a volume, a cell in a grid-based computation).

To manage hundreds of threads running several different programs, the multiprocessor employs a new architecture we call SIMT (single-instruction, multiple-thread). The multiprocessor maps each thread to one scalar processor core, and each scalar thread executes independently with its own instruction address and register state. The multiprocessor SIMT unit creates, manages, schedules, and executes threads in groups of parallel threads called warps. (This term originates from weaving, the first parallel thread technology.) Individual threads composing a SIMT warp start together at the same program address but are otherwise free to branch and execute independently.

When a multiprocessor is given one or more thread blocks to execute, it splits them into warps that get scheduled by the SIMT unit. The way a block is split into warps is always the same; each warp contains threads of consecutive, increasing thread IDs with the first warp containing thread 0.

At every instruction issue time, the SIMT unit selects a warp that is ready to execute and issues the next instruction to the active threads of the warp. A warp executes one common instruction at a time, so full efficiency is realized when all threads of a warp agree on their execution path. If threads of a warp diverge via a data-dependent conditional branch, the warp serially executes each branch path taken, disabling threads that are not on that path, and when all paths complete, the threads converge back to the same execution path. Branch divergence occurs only within a warp; different warps execute independently regardless of whether they are executing common or disjointed code paths.

SIMT architecture is akin to SIMD (Single Instruction, Multiple Data) vector organizations in that a single instruction controls multiple processing elements. A key difference is that SIMD vector organizations expose the SIMD width to the software, whereas SIMT instructions specify the execution and branching behavior of a single thread. In contrast with SIMD vector machines, SIMT enables programmers to write thread-level parallel code for independent, scalar threads, as well as data-parallel code for coordinated threads. For the purposes of correctness, the programmer can essentially ignore the SIMT behavior; however, substantial performance improvements can be realized by taking care that the code seldom requires threads in a warp to diverge. In practice, this is analogous to the role of cache lines in traditional code: Cache line size can be safely ignored when designing for correctness but must be considered in the code structure when designing for peak performance. Vector architectures, on the other hand, require the software to coalesce loads into vectors and manage divergence manually.

As illustrated by Figure 3,each multiprocessor has on-chip memory of the four following types:

  • One set of local 32-bit registers per processor,
  • A parallel data cache or shared memory that is shared by all scalar processor cores and is where the shared memory space resides,
  • A read-only constant cache that is shared by all scalar processor cores and speeds up reads from the constant memory space, which is a read-only region of device memory,
  • A read-only texture cache that is shared by all scalar processor cores and speeds up reads from the texture memory space, which is a read-only region of device memory; each multiprocessor accesses the texture cache via a texture unit that implements the various addressing modes and data filtering.

The local and global memory spaces are read-write regions of device memory and are not cached.

How many blocks a multiprocessor can process at once depends on how many registers per thread and how much shared memory per block are required for a given kernel since the multiprocessor's registers and shared memory are split among all the threads of the batch of blocks. If there are not enough registers or shared memory available per multiprocessor to process at least one block, the kernel will fail to launch.

Figure 3. Hardware ModelSet of SIMT Multiprocessors
Note: A set of SIMT multiprocessors with on-chip shared memory.

4. Syntax

PTX programs are a collection of text source modules (files). PTX source modules have an assembly-language style syntax with instruction operation codes and operands. Pseudo-operations specify symbol and addressing management. The ptxas optimizing backend compiler optimizes and assembles PTX source modules to produce corresponding binary object files.

4.1. Source Format

Source modules are ASCII text. Lines are separated by the newline character (\n).

All whitespace characters are equivalent; whitespace is ignored except for its use in separating tokens in the language.

The C preprocessor cpp may be used to process PTX source modules. Lines beginning with # are preprocessor directives. The following are common preprocessor directives:

#include, #define, #if, #ifdef, #else, #endif, #line, #file

C: A Reference Manual by Harbison and Steele provides a good description of the C preprocessor.

PTX is case sensitive and uses lowercase for keywords.

Each PTX module must begin with a .version directive specifying the PTX language version, followed by a .target directive specifying the target architecture assumed. See PTX Module Directives for a more information on these directives.

4.2. Comments

Comments in PTX follow C/C++ syntax, using non-nested /* and */ for comments that may span multiple lines, and using // to begin a comment that extends up to the next newline character, which terminates the current line. Comments cannot occur within character constants, string literals, or within other comments.

Comments in PTX are treated as whitespace.

4.3. Statements

A PTX statement is either a directive or an instruction. Statements begin with an optional label and end with a semicolon.

Examples

        .reg     .b32 r1, r2; 
        .global  .f32  array[N]; 

start:  mov.b32   r1, %tid.x;
        shl.b32   r1, r1, 2;          // shift thread id by 2 bits
        ld.global.b32 r2, array[r1];  // thread[tid] gets array[tid]
        add.f32   r2, r2, 0.5;        // add 1/2

4.3.1. Directive Statements

Directive keywords begin with a dot, so no conflict is possible with user-defined identifiers. The directives in PTX are listed in Table 1 and described in State Spaces, Types, and Variables and Directives.

Table 1. PTX Directives
.address_size .file .minnctapersm .target
.align .func .param .tex
.branchtargets .global .pragma .version
.callprototype .loc .reg .visible
.calltargets .local .reqntid .weak
.const .maxnctapersm .section  
.entry .maxnreg .shared  
.extern .maxntid .sreg  

4.3.2. Instruction Statements

Instructions are formed from an instruction opcode followed by a comma-separated list of zero or more operands, and terminated with a semicolon. Operands may be register variables, constant expressions, address expressions, or label names. Instructions have an optional guard predicate which controls conditional execution. The guard predicate follows the optional label and precedes the opcode, and is written as @p, where p is a predicate register. The guard predicate may be optionally negated, written as @!p.

The destination operand is first, followed by source operands.

Instruction keywords are listed in Table 2.All instruction keywords are reserved tokens in PTX.

Table 2. Reserved Instruction Keywords
abs div or sin vavrg2, vavrg4
add ex2 pmevent slct vmad
addc exit popc sqrt vmax
and fma prefetch st vmax2, vmax4
atom isspacep prefetchu sub vmin
bar ld prmt subc vmin2, vmin4
bfe ldu rcp suld vote
bfi lg2 red suq vset
bfind mad rem sured vset2, vset4
bra mad24 ret sust vshl
brev madc rsqrt testp vshr
brkpt max sad tex vsub
call membar selp tld4 vsub2, vsub4
clz min set trap xor
cnot mov setp txq  
copysign mul shf vabsdiff  
cos mul 24 shfl vabsdiff2, vabsdiff4  
cvt neg shl vadd  
cvta not shr vadd2, vadd4  

4.4. Identifiers

User-defined identifiers follow extended C++ rules: they either start with a letter followed by zero or more letters, digits, underscore, or dollar characters; or they start with an underscore, dollar, or percentage character followed by one or more letters, digits, underscore, or dollar characters: 

      followsym:   [a-zA-Z0-9_$]
      identifier:  [a-zA-Z]{followsym}* | {[_$%]{followsym}+

PTX does not specify a maximum length for identifiers and suggests that all implementations support a minimum length of at least 1024 characters.

Many high-level languages such as C and C++ follow similar rules for identifier names, except that the percentage sign is not allowed. PTX allows the percentage sign as the first character of an identifier. The percentage sign can be used to avoid name conflicts, e.g., between user-defined variable names and compiler-generated names.

PTX predefines one constant and a small number of special registers that begin with the percentage sign, listed in Table 3.

Table 3. Predefined Identifiers
%clock %laneid %lanemask_gt %pm0, ..., %pm7
%clock64 %lanemask_eq %nctaid %smid
%ctaid %lanemask_le %ntid %tid
%envreg<32> %lanemask_lt %nsmid %warpid
%gridid %lanemask_ge %nwarpid WARP_SZ

4.5. Constants

PTX supports integer and floating-point constants and constant expressions. These constants may be used in data initialization and as operands to instructions. Type checking rules remain the same for integer, floating-point, and bit-size types. For predicate-type data and instructions, integer constants are allowed and are interpreted as in C, i.e., zero values are False and non-zero values are True.

4.6. Integer Constants

Integer constants are 64-bits in size and are either signed or unsigned, i.e., every integer constant has type .s64 or .u64. The signed/unsigned nature of an integer constant is needed to correctly evaluate constant expressions containing operations such as division and ordered comparisons, where the behavior of the operation depends on the operand types. When used in an instruction or data initialization, each integer constant is converted to the appropriate size based on the data or instruction type at its use.

Integer literals may be written in decimal, hexadecimal, octal, or binary notation. The syntax follows that of C. Integer literals may be followed immediately by the letter U to indicate that the literal is unsigned. 

      hexadecimal literal:  0[xX]{hexdigit}+U?
      octal literal:        0{octal digit}+U?
      binary literal:       0[bB]{bit}+U?
      decimal literal       {nonzero-digit}{digit}*U?

Integer literals are non-negative and have a type determined by their magnitude and optional type suffix as follows: literals are signed (.s64) unless the value cannot be fully represented in .s64 or the unsigned suffix is specified, in which case the literal is unsigned (.u64).

The predefined integer constant WARP_SZ specifies the number of threads per warp for the target platform; to date, all target architectures have a WARP_SZ value of 32.

4.6.1. Floating-Point Constants

Floating-point constants are represented as 64-bit double-precision values, and all floating-point constant expressions are evaluated using 64-bit double precision arithmetic. The only exception is the 32-bit hex notation for expressing an exact single-precision floating-point value; such values retain their exact 32-bit single-precision value and may not be used in constant expressions. Each 64-bit floating-point constant is converted to the appropriate floating-point size based on the data or instruction type at its use.

Floating-point literals may be written with an optional decimal point and an optional signed exponent. Unlike C and C++, there is no suffix letter to specify size; literals are always represented in 64-bit double-precision format.

PTX includes a second representation of floating-point constants for specifying the exact machine representation using a hexadecimal constant. To specify IEEE 754 double-precision floating point values, the constant begins with 0d or 0D followed by 16 hex digits. To specify IEEE 754 single-precision floating point values, the constant begins with 0f or 0F followed by 8 hex digits. 

0[fF]{hexdigit}{8}      // single-precision floating point
0[dD]{hexdigit}{16}     // double-precision floating point

Example

      mov.f32  $f3, 0F3f800000;       //  1.0

4.6.2. Predicate Constants

In PTX, integer constants may be used as predicates. For predicate-type data initializers and instruction operands, integer constants are interpreted as in C, i.e., zero values are False and non-zero values are True.

4.6.3. Constant Expressions

In PTX, constant expressions are formed using operators as in C and are evaluated using rules similar to those in C, but simplified by restricting types and sizes, removing most casts, and defining full semantics to eliminate cases where expression evaluation in C is implementation dependent.

Constant expressions are formed from constant literals, unary plus and minus, basic arithmetic operators (addition, subtraction, multiplication, division), comparison operators, the conditional ternary operator ( ?: ), and parentheses. Integer constant expressions also allow unary logical negation (!), bitwise complement (~), remainder (%), shift operators (<< and >>), bit-type operators (&, |, and ^), and logical operators (&&, ||).

Constant expressions in PTX do not support casts between integer and floating-point.

Constant expressions are evaluated using the same operator precedence as in C. Table 4 gives operator precedence and associativity. Operator precedence is highest for unary operators and decreases with each line in the chart. Operators on the same line have the same precedence and are evaluated right-to-left for unary operators and left-to-right for binary operators.

Table 4. Operator Precedence
Kind Operator Symbols Operator Names Associates
Primary () parenthesis n/a
Unary +- ! ~ plus, minus, negation, complement right
(.s64)(.u64) casts right
Binary */ % multiplication, division, remainder left
+- addition, subtraction
>> << shifts
< > <= >= ordered comparisons
== != equal, not equal
& bitwise AND
^ bitwise XOR
| bitwise OR
&& logical AND
|| logical OR
Ternary ?: conditional right

4.6.4. Integer Constant Expression Evaluation

Integer constant expressions are evaluated at compile time according to a set of rules that determine the type (signed .s64 versus unsigned .u64) of each sub-expression.  These rules are based on the rules in C, but they've been simplified to apply only to 64-bit integers, and behavior is fully defined in all cases (specifically, for remainder and shift operators).

  • Literals are signed unless unsigned is needed to prevent overflow, or unless the literal uses a U suffix. For example:
    • 42, 0x1234, 0123 are signed.
    • 0xfabc123400000000, 42U, 0x1234U are unsigned.
  • Unary plus and minus preserve the type of the input operand. For example:
    • +123, -1, -(-42) are signed.
    • -1U, -0xfabc123400000000 are unsigned.
  • Unary logical negation (!) produces a signed result with value 0 or 1.
  • Unary bitwise complement (~) interprets the source operand as unsigned and produces an unsigned result.
  • Some binary operators require normalization of source operands. This normalization is known as the usual arithmetic conversions and simply converts both operands to unsigned type if either operand is unsigned.
  • Addition, subtraction, multiplication, and division perform the usual arithmetic conversions and produce a result with the same type as the converted operands.  That is, the operands and result are unsigned if either source operand is unsigned, and is otherwise signed.
  • Remainder (%) interprets the operands as unsigned. Note that this differs from C, which allows a negative divisor but defines the behavior to be implementation dependent.
  • Left and right shift interpret the second operand as unsigned and produce a result with the same type as the first operand. Note that the behavior of right-shift is determined by the type of the first operand: right shift of a signed value is arithmetic and preserves the sign, and right shift of an unsigned value is logical and shifts in a zero bit.
  • AND (&), OR (|), and XOR (^) perform the usual arithmetic conversions and produce a result with the same type as the converted operands.
  • AND_OP (&&), OR_OP (||), Equal (==), and Not_Equal (!=) produce a signed result. The result value is 0 or 1.
  • Ordered comparisons (<, <=, >, >=) perform the usual arithmetic conversions on source operands and produce a signed result. The result value is 0 or 1.
  • Casting of expressions to signed or unsigned is supported using (.s64) and (.u64) casts.
  • For the conditional operator ( ? : ) , the first operand must be an integer, and the second and third operands are either both integers or both floating-point. The usual arithmetic conversions are performed on the second and third operands, and the result type is the same as the converted type.

4.6.5. Summary of Constant Expression Evaluation Rules

Table 5 contains a summary of the constant expression evaluation rules.

Table 5. Constant Expression Evaluation Rules
Kind Operator Operand Types Operand Interpretation Result Type
Primary () any type same as source same as source
constant literal n/a n/a .u64, .s64, or .f64
Unary +- any type same as source same as source
! integer zero or non-zero .s64
~ integer .u64 .u64
Cast (.u64) integer .u64 .u64
(.s64) integer .s64 .s64
Binary +- * / .f64 .f64 .f64
integer use usual conversions converted type
< > <= >= .f64 .f64 .s64
integer use usual conversions .s64
== != .f64 .f64 .s64
integer use usual conversions .s64
% integer .u64 .s64
>> << integer 1st unchanged, 2nd is .u64 same as 1st operand
& | ^ integer .u64 .u64
&& || integer zero or non-zero .s64
Ternary ?: int ? .f64 : .f64 same as sources .f64
int ? int : int use usual conversions converted type

5. State Spaces, Types, and Variables

While the specific resources available in a given target GPU will vary, the kinds of resources will be common across platforms, and these resources are abstracted in PTX through state spaces and data types.

5.1. State Spaces

A state space is a storage area with particular characteristics. All variables reside in some state space. The characteristics of a state space include its size, addressability, access speed, access rights, and level of sharing between threads.

The state spaces defined in PTX are a byproduct of parallel programming and graphics programming. The list of state spaces is shown in Table 6,and properties of state spaces are shown in Table 7.

Table 6. State Spaces
Name Description
.reg Registers, fast.
.sreg Special registers. Read-only; pre-defined; platform-specific.
.const Shared, read-only memory.
.global Global memory, shared by all threads.
.local Local memory, private to each thread.
.param

Kernel parameters, defined per-grid; or

Function or local parameters, defined per-thread.
.shared Addressable memory shared between threads in 1 CTA.
.tex Global texture memory (deprecated).
Table 7. Properties of State Spaces
Name Addressable Initializable Access Sharing
.reg No No R/W per-thread
.sreg No No RO per-CTA
.const Yes Yes1 RO per-grid
.global Yes Yes1 R/W Context
.local Yes No R/W per-thread
.param (as input to kernel) Yes2 No RO per-grid
.param (used in functions) Restricted3 No R/W per-thread
.shared Yes No R/W per-CTA
.tex No4 Yes, via driver RO Context

Notes:

1 Variables in .const and .global state spaces are initialized to zero by default.

2 Accessible only via the ld.param instruction. Address may be taken via mov instruction.

3 Accessible via ld.param and st.param instructions. Device function input and return parameters may have their address taken via mov; the parameter is then located on the stack frame and its address is in the .local state space.

4 Accessible only via the tex instruction.

5.1.1. Register State Space

Registers (.reg state space) are fast storage locations. The number of registers is limited, and will vary from platform to platform. When the limit is exceeded, register variables will be spilled to memory, causing changes in performance. For each architecture, there is a recommended maximum number of registers to use (see the CUDA Programming Guide for details).

Registers may be typed (signed integer, unsigned integer, floating point, predicate) or untyped. Register size is restricted; aside from predicate registers which are 1-bit, scalar registers have a width of 8-, 16-, 32-, or 64-bits, and vector registers have a width of 16-, 32-, 64-, or 128-bits. The most common use of 8-bit registers is with ld, st, and cvt instructions, or as elements of vector tuples.

Registers differ from the other state spaces in that they are not fully addressable, i.e., it is not possible to refer to the address of a register. When compiling to use the Application Binary Interface (ABI), register variables are restricted to function scope and may not be declared at module scope. When compiling legacy PTX code (ISA versions prior to 3.0) containing module-scoped .reg variables, the compiler silently disables use of the ABI. Registers may have alignment boundaries required by multi-word loads and stores.

5.1.2. Special Register State Space

The special register (.sreg) state space holds predefined, platform-specific registers, such as grid, CTA, and thread parameters, clock counters, and performance monitoring registers. All special registers are predefined.

5.1.3. Constant State Space

The constant (.const) state space is a read-only memory initialized by the host. Constant memory is accessed with a ld.const instruction. Constant memory is restricted in size, currently limited to 64 KB which can be used to hold statically-sized constant variables. There is an additional 640 KB of constant memory, organized as ten independent 64 KB regions. The driver may allocate and initialize constant buffers in these regions and pass pointers to the buffers as kernel function parameters. Since the ten regions are not contiguous, the driver must ensure that constant buffers are allocated so that each buffer fits entirely within a 64 KB region and does not span a region boundary.

Statically-sized constant variables have an optional variable initializer; constant variables with no explicit initializer are initialized to zero by default. Constant buffers allocated by the driver are initialized by the host, and pointers to such buffers are passed to the kernel as parameters. See the description of kernel parameter attributes in Kernel Function Parameter Attributes for more details on passing pointers to constant buffers as kernel parameters.

5.1.3.1. Banked Constant State Space (deprecated)

Previous versions of PTX exposed constant memory as a set of eleven 64 KB banks, with explicit bank numbers required for variable declaration and during access.

Prior to PTX ISA version 2.2, the constant memory was organized into fixed size banks. There were eleven 64 KB banks, and banks were specified using the .const[bank] modifier, where bank ranged from 0 to 10. If no bank number was given, bank zero was assumed.

By convention, bank zero was used for all statically-sized constant variables. The remaining banks were used to declare incomplete constant arrays (as in C, for example), where the size is not known at compile time. For example, the declaration 
.extern .const[2] .b32 const_buffer[];
resulted in const_buffer pointing to the start of constant bank two. This pointer could then be used to access the entire 64 KB constant bank. Multiple incomplete array variables declared in the same bank were aliased, with each pointing to the start address of the specified constant bank.
To access data in contant banks 1 through 10, the bank number was required in the state space of the load instruction. For example, an incomplete array in bank 2 was accessed as follows: 
.extern .const[2] .b32 const_buffer[];
ld.const[2].b32  %r1, [const_buffer+4]; // load second word
In PTX ISA version 2.2, we eliminated explicit banks and replaced the incomplete array representation of driver-allocated constant buffers with kernel parameter attributes that allow pointers to constant buffers to be passed as kernel parameters.

5.1.4. Global State Space

The global (.global) state space is memory that is accessible by all threads in a context. It is the mechanism by which different CTAs and different grids can communicate. Use ld.global, st.global, and atom.global to access global variables.

Global variables have an optional variable initializer; global variables with no explicit initializer are initialized to zero by default.

5.1.5. Local State Space

The local state space (.local) is private memory for each thread to keep its own data. It is typically standard memory with cache. The size is limited, as it must be allocated on a per-thread basis. Use ld.local and st.local to access local variables.

When compiling to use the Application Binary Interface (ABI), .local state-space variables must be declared within function scope and are allocated on the stack. In implementations that do not support a stack, all local memory variables are stored at fixed addresses, recursive function calls are not supported, and .local variables may be declared at module scope. When compiling legacy PTX code (ISA versions prior to 3.0) containing module-scoped .local variables, the compiler silently disables use of the ABI.

5.1.6. Parameter State Space

The parameter (.param) state space is used (1) to pass input arguments from the host to the kernel, (2a) to declare formal input and return parameters for device functions called from within kernel execution, and (2b) to declare locally-scoped byte array variables that serve as function call arguments, typically for passing large structures by value to a function. Kernel function parameters differ from device function parameters in terms of access and sharing (read-only versus read-write, per-kernel versus per-thread). Note that PTX ISA versions 1.x supports only kernel function parameters in .param space; device function parameters were previously restricted to the register state space. The use of parameter state space for device function parameters was introduced in PTX ISA version 2.0 and requires target architecture sm_20 or higher.

Note: The location of parameter space is implementation specific. For example, in some implementations kernel parameters reside in global memory. No access protection is provided between parameter and global space in this case. Similarly, function parameters are mapped to parameter passing registers and/or  stack locations based on the function calling conventions of the Application Binary Interface (ABI). Therefore, PTX code should make no assumptions about the relative locations or ordering of .param space variables.

5.1.6.1. Kernel Function Parameters

Each kernel function definition includes an optional list of parameters. These parameters are addressable, read-only variables declared in the .param state space. Values passed from the host to the kernel are accessed through these parameter variables using ld.param instructions. The kernel parameter variables are shared across all CTAs within a grid.

The address of a kernel parameter may be moved into a register using the mov instruction. The resulting address is in the .param state space and is accessed using ld.param instructions.

Example
.entry foo ( .param .b32 N, .param .align 8 .b8 buffer[64] )
{
    .reg .u32 %n;
    .reg .f64 %d;

    ld.param.u32 %n, [N];  
    ld.param.f64 %d, [buffer];
    ...
Example
.entry bar ( .param .b32 len )
{
    .reg .u32 %ptr, %n;

    mov.u32      %ptr, len;
    ld.param.u32 %n, [%ptr];
    ...

Kernel function parameters may represent normal data values, or they may hold addresses to objects in constant, global, local, or shared state spaces. In the case of pointers, the compiler and runtime system need information about which parameters are pointers, and to which state space they point. Kernel parameter attribute directives are used to provide this information at the PTX level. See Kernel Function Parameter Attributes for a description of kernel parameter attribute directives.

Note: The current implementation does not allow creation of generic pointers to constant variables (cvta.const) in programs that have pointers to constant buffers passed as kernel parameters.

5.1.6.2. Kernel Function Parameter Attributes

Kernel function parameters may be declared with an optional .ptr attribute to indicate that a parameter is a pointer to memory, and also indicate the state space and alignment of the memory being pointed to. Kernel Parameter Attribute: .ptr describes the .ptr kernel parameter attribute.

5.1.6.3. Kernel Parameter Attribute: .ptr

.ptr

Kernel parameter alignment attribute.

Syntax
.param .type .ptr .space .align N  varname
.param .type .ptr        .align N  varname

.space = { .const, .global, .local, .shared };
Description

Used to specify the state space and, optionally, the alignment of memory pointed to by a pointer type kernel parameter. The alignment value N, if present, must be a power of two. If no state space is specified, the pointer is assumed to be a generic address pointing to one of const, global, local, or shared memory. If no alignment is specified, the memory pointed to is assumed to be aligned to a 4 byte boundary.

Spaces between .ptr, .space, and .align may be eliminated to improve readability.

PTX ISA Notes
  • Introduced in PTX ISA version 2.2.
  • Support for generic addressing of .const space added in PTX ISA version 3.1.
Target ISA Notes
  • Supported on all target architectures.
Examples
.entry foo ( .param .u32 param1,
             .param .u32 .ptr.global.align 16 param2,
             .param .u32 .ptr.const.align 8 param3,
             .param .u32 .ptr.align 16 param4  // generic address
                                               // pointer
) { .. }

5.1.6.4. Device Function Parameters

PTX ISA version 2.0 extended the use of parameter space to device function parameters. The most common use is for passing objects by value that do not fit within a PTX register, such as C structures larger than 8 bytes. In this case, a byte array in parameter space is used. Typically, the caller will declare a locally-scoped .param byte array variable that represents a flattened C structure or union. This will be passed by value to a callee, which declares a .param formal parameter having the same size and alignment as the passed argument.

Example
// pass object of type struct { double d; int y; };
.func foo ( .reg .b32 N, .param .align 8 .b8 buffer[12] )
{
    .reg .f64 %d;
    .reg .s32 %y;

    ld.param.f64 %d, [buffer];
    ld.param.s32 %y, [buffer+8];
    ...
}

// code snippet from the caller
// struct { double d; int y; } mystruct; is flattened, passed to foo
    ...
    .reg .f64 dbl;
    .reg .s32 x;
    .param .align 8 .b8 mystruct;  
    ...
    st.param.f64 [mystruct+0], dbl;
    st.param.s32 [mystruct+8], x;
    call foo, (4, mystruct);
    ...

See the section on function call syntax for more details.

Function input parameters may be read via ld.param and function return parameters may be written using st.param; it is illegal to write to an input parameter or read from a return parameter.

Aside from passing structures by value, .param space is also required whenever a formal parameter has its address taken within the called function. In PTX, the address of a function input parameter may be moved into a register using the mov instruction. Note that the parameter will be copied to the stack if necessary, and so the address will be in the .local state space and is accessed via ld.local and st.local instructions. It is not possible to use mov to get the address of or a locally-scoped .param space variable. Starting PTX ISA version 6.0, it is possible to use mov instruction to get address of return parameter of device function.

Example
// pass array of up to eight floating-point values in buffer
.func foo ( .param .b32 N, .param .b32 buffer[32] )
{
    .reg .u32  %n, %r;
    .reg .f32  %f;
    .reg .pred %p;

    ld.param.u32 %n, [N];
    mov.u32      %r, buffer;  // forces buffer to .local state space
Loop:
    setp.eq.u32  %p, %n, 0;
@p: bra          Done;
    ld.local.f32 %f, [%r];
    ... 
    add.u32      %r, %r, 4;
    sub.u32      %n, %n, 1;
    bra          Loop;
Done:
    ...
}

5.1.7. Shared State Space

The shared (.shared) state space is a per-CTA region of memory for threads in a CTA to share data. An address in shared memory can be read and written by any thread in a CTA. Use ld.shared and st.shared to access shared variables.

Shared memory typically has some optimizations to support the sharing. One example is broadcast; where all threads read from the same address. Another is sequential access from sequential threads.

5.1.8. Texture State Space (deprecated)

The texture (.tex) state space is global memory accessed via the texture instruction. It is shared by all threads in a context. Texture memory is read-only and cached, so accesses to texture memory are not coherent with global memory stores to the texture image.

The GPU hardware has a fixed number of texture bindings that can be accessed within a single kernel (typically 128). The .tex directive will bind the named texture memory variable to a hardware texture identifier, where texture identifiers are allocated sequentially beginning with zero. Multiple names may be bound to the same physical texture identifier. An error is generated if the maximum number of physical resources is exceeded. The texture name must be of type .u32 or .u64.

Physical texture resources are allocated on a per-kernel granularity, and .tex variables are required to be defined in the global scope.

Texture memory is read-only. A texture's base address is assumed to be aligned to a 16 byte boundary.

Example

    .tex .u32 tex_a;         // bound to physical texture 0
    .tex .u32 tex_c, tex_d;  // both bound to physical texture 1
    .tex .u32 tex_d;         // bound to physical texture 2
    .tex .u32 tex_f;         // bound to physical texture 3
Note: Explicit declarations of variables in the texture state space is deprecated, and programs should instead reference texture memory through variables of type .texref. The .tex directive is retained for backward compatibility, and variables declared in the .tex state space are equivalent to module-scoped .texref variables in the .global state space.
For example, a legacy PTX definitions such as 
    .tex .u32 tex_a;
is equivalent to: 
    .global .texref tex_a;

See Texture Sampler and Surface Types for the description of the .texref type and Texture Instructions for its use in texture instructions.

5.2. Types

5.2.1. Fundamental Types

In PTX, the fundamental types reflect the native data types supported by the target architectures. A fundamental type specifies both a basic type and a size. Register variables are always of a fundamental type, and instructions operate on these types.  The same type-size specifiers are used for both variable definitions and for typing instructions, so their names are intentionally short.

Table 8 lists the fundamental type specifiers for each basic type:

Table 8. Fundamental Type Specifiers
Basic Type Fundamental Type Specifiers
Signed integer .s8, .s16, .s32, .s64
Unsigned integer .u8, .u16, .u32, .u64
Floating-point .f16, .f16x2, .f32, .f64
Bits (untyped) .b8, .b16, .b32, .b64
Predicate .pred

Most instructions have one or more type specifiers, needed to fully specify instruction behavior. Operand types and sizes are checked against instruction types for compatibility.

Two fundamental types are compatible if they have the same basic type and are the same size. Signed and unsigned integer types are compatible if they have the same size. The bit-size type is compatible with any fundamental type having the same size.

In principle, all variables (aside from predicates) could be declared using only bit-size types, but typed variables enhance program readability and allow for better operand type checking.

5.2.2. Restricted Use of Sub-Word Sizes

The .u8, .s8, and .b8 instruction types are restricted to ld, st, and cvt instructions. The .f16 floating-point type is allowed only in conversions to and from .f32, .f64 types, in half precision floating point instructions and texture fetch instructions. The .f16x2 floating point type is allowed only in half precision floating point arithmetic instructions and texture fetch instructions.

For convenience, ld, st, and cvt instructions permit source and destination data operands to be wider than the instruction-type size, so that narrow values may be loaded, stored, and converted using regular-width registers. For example, 8-bit or 16-bit values may be held directly in 32-bit or 64-bit registers when being loaded, stored, or converted to other types and sizes.

5.3. Texture Sampler and Surface Types

PTX includes built-in opaque types for defining texture, sampler, and surface descriptor variables. These types have named fields similar to structures, but all information about layout, field ordering, base address, and overall size is hidden to a PTX program, hence the term opaque. The use of these opaque types is limited to:

  • Variable definition within global (module) scope and in kernel entry parameter lists.
  • Static initialization of module-scope variables using comma-delimited static assignment expressions for the named members of the type.
  • Referencing textures, samplers, or surfaces via texture and surface load/store instructions (tex, suld, sust, sured).
  • Retrieving the value of a named member via query instructions (txq, suq).
  • Creating pointers to opaque variables using mov, e.g., mov.u64 reg, opaque_var;. The resulting pointer may be stored to and loaded from memory, passed as a parameter to functions, and de-referenced by texture and surface load, store, and query instructions, but the pointer cannot otherwise be treated as an address, i.e., accessing the pointer with ld and st instructions, or performing pointer arithmetic will result in undefined results.
  • Opaque variables may not appear in initializers, e.g., to initialize a pointer to an opaque variable.
Note:

Indirect access to textures and surfaces using pointers to opaque variables is supported beginning with PTX ISA version 3.1 and requires target sm_20 or later.

Indirect access to textures is supported only in unified texture mode (see below).

The three built-in types are .texref, .samplerref, and .surfref. For working with textures and samplers, PTX has two modes of operation. In the unified mode, texture and sampler information is accessed through a single .texref handle. In the independent mode, texture and sampler information each have their own handle, allowing them to be defined separately and combined at the site of usage in the program. In independent mode, the fields of the .texref type that describe sampler properties are ignored, since these properties are defined by .samplerref variables.

Table 9 and Table 10 list the named members of each type for unified and independent texture modes. These members and their values have precise mappings to methods and values defined in the texture HW class as well as exposed values via the API.

Table 9. Opaque Type Fields in Unified Texture Mode
Member .texref values .surfref values
width in elements
height in elements
depth in elements
channel_data_type enum type corresponding to source language API
channel_order enum type corresponding to source language API
normalized_coords 0, 1 N/A
filter_mode nearest, linear N/A
addr_mode_0, addr_mode_1, addr_mode_2 wrap,mirror, clamp_ogl, clamp_to_edge, clamp_to_border N/A
array_size as number of textures in a texture array as number of surfaces in a surface array
num_mipmap_levels as number of levels in a mipmapped texture N/A
num_samples as number of samples in a multi-sample texture N/A
memory_layout N/A 1 for linear memory layout; 0 otherwise

Texture and Surface Properties

Fields width, height, and depth specify the size of the texture or surface in number of elements in each dimension.

The channel_data_type and channel_order fields specify these properties of the texture or surface using enumeration types corresponding to the source language API. For example, see Channel Data Type and Channel Order Fields for the OpenCL enumeration types currently supported in PTX.

5.3.2. Sampler Properties

The normalized_coords field indicates whether the texture or surface uses normalized coordinates in the range [0.0, 1.0) instead of unnormalized coordinates in the range [0, N). If no value is specified, the default is set by the runtime system based on the source language.

The filter_mode field specifies how the values returned by texture reads are computed based on the input texture coordinates.

The addr_mode_{0,1,2} fields define the addressing mode in each dimension, which determine how out-of-range coordinates are handled.

See the CUDA C Programming Guide for more details of these properties.

Table 10. Opaque Type Fields in Independent Texture Mode
Member .samplerref values .texref values .surfref values
width N/A in elements
height N/A in elements
depth N/A in elements
channel_data_type N/A enum type corresponding to source language API
channel_order N/A enum type corresponding to source language AP
normalized_coords N/A 0, 1 N/A
force_unnormalized_coords 0, 1 N/A N/A
filter_mode nearest, linear ignored N/A
addr_mode_0, addr_mode_1, addr_mode_2 wrap,mirror, clamp_ogl, clamp_to_edge, clamp_to_border N/A
array_size N/A as number of textures in a texture array as number of surfaces in a surface array
num_mipmap_levels N/A as number of levels in a mipmapped texture N/A
num_samples N/A as number of samples in a multi-sample texture N/A
memory_layout N/A N/A 1 for linear memory layout; 0 otherwise

In independent texture mode, the sampler properties are carried in an independent .samplerref variable, and these fields are disabled in the .texref variables. One additional sampler property, force_unnormalized_coords, is available in independent texture mode.

The force_unnormalized_coords field is a property of .samplerref variables that allows the sampler to override the texture header normalized_coords property. This field is defined only in independent texture mode. When True, the texture header setting is overridden and unnormalized coordinates are used; when False, the texture header setting is used.

The force_unnormalized_coords property is used in compiling OpenCL; in OpenCL, the property of normalized coordinates is carried in sampler headers. To compile OpenCL to PTX, texture headers are always initialized with normalized_coords set to True, and the OpenCL sampler-based normalized_coords flag maps (negated) to the PTX-level force_unnormalized_coords flag.

Variables using these types may be declared at module scope or within kernel entry parameter lists. At module scope, these variables must be in the .global state space.  As kernel parameters, these variables are declared in the .param state space.

Example

      .global .texref     my_texture_name;
      .global .samplerref my_sampler_name;
      .global .surfref    my_surface_name;

When declared at module scope, the types may be initialized using a list of static expressions assigning values to the named members.

Example

      .global .texref tex1;
      .global .samplerref tsamp1 = { addr_mode_0 = clamp_to_border, 
                                     filter_mode = nearest
                                   };

5.3.3. Channel Data Type and Channel Order Fields

The channel_data_type and channel_order fields have enumeration types corresponding to the source language API. Currently, OpenCL is the only source language that defines these fields. Table 12 and Table 11 show the enumeration values defined in OpenCL version 1.0 for channel data type and channel order.

Table 11. OpenCL 1.0 Channel Data Type Definition
CL_SNORM_INT8 0x10D0
CL_SNORM_INT16 0x10D1
CL_UNORM_INT8 0x10D2
CL_UNORM_INT16 0x10D3
CL_UNORM_SHORT_565 0x10D4
CL_UNORM_SHORT_555 0x10D5
CL_UNORM_INT_101010 0x10D6
CL_SIGNED_INT8 0x10D7
CL_SIGNED_INT16 0x10D8
CL_SIGNED_INT32 0x10D9
CL_UNSIGNED_INT8 0x10DA
CL_UNSIGNED_INT16 0x10DB
CL_UNSIGNED_INT32 0x10DC
CL_HALF_FLOAT 0x10DD
CL_FLOAT 0x10DE
Table 12. OpenCL 1.0 Channel Order Definition
CL_R 0x10B0
CL_A 0x10B1
CL_RG 0x10B2
CL_RA 0x10B3
CL_RGB 0x10B4
CL_RGBA 0x10B5
CL_BGRA 0x10B6
CL_ARGB 0x10B7
CL_INTENSITY 0x10B8
CL_LUMINANCE 0x10B9

5.4. Variables

In PTX, a variable declaration describes both the variable's type and its state space.  In addition to fundamental types, PTX supports types for simple aggregate objects such as vectors and arrays.

5.4.1. Variable Declarations

All storage for data is specified with variable declarations. Every variable must reside in one of the state spaces enumerated in the previous section.

A variable declaration names the space in which the variable resides, its type and size, its name, an optional array size, an optional initializer, and an optional fixed address for the variable.

Predicate variables may only be declared in the register state space.

Examples

      .global .u32 loc;
      .reg    .s32 i;
      .const  .f32 bias[] = {-1.0, 1.0};
      .global .u8  bg[4] = {0, 0, 0, 0};
      .reg    .v4 .f32 accel;
      .reg    .pred p, q, r;

5.4.2. Vectors

Limited-length vector types are supported. Vectors of length 2 and 4 of any non-predicate fundamental type can be declared by prefixing the type with .v2 or .v4. Vectors must be based on a fundamental type, and they may reside in the register space. Vectors cannot exceed 128-bits in length; for example, .v4.f64 is not allowed. Three-element vectors may be handled by using a .v4 vector, where the fourth element provides padding. This is a common case for three-dimensional grids, textures, etc.

Examples

      .global .v4 .f32 V;   // a length-4 vector of floats
      .shared .v2 .u16 uv;  // a length-2 vector of unsigned ints
      .global .v4 .b8  v;   // a length-4 vector of bytes

By default, vector variables are aligned to a multiple of their overall size (vector length times base-type size), to enable vector load and store instructions which require addresses aligned to a multiple of the access size.

5.4.3. Array Declarations

Array declarations are provided to allow the programmer to reserve space. To declare an array, the variable name is followed with dimensional declarations similar to fixed-size array declarations in C. The size of each dimension is a constant expression.

Examples

      .local  .u16 kernel[19][19];
      .shared .u8  mailbox[128];

The size of the array specifies how many elements should be reserved. For the declaration of array kernel above, 19*19 = 361 halfwords are reserved, for a total of 722 bytes.

When declared with an initializer, the first dimension of the array may be omitted. The size of the first array dimension is determined by the number of elements in the array initializer.

Examples

      .global .u32 index[] = { 0, 1, 2, 3, 4, 5, 6, 7 };
      .global .s32 offset[][2] = { {-1, 0}, {0, -1}, {1, 0}, {0, 1} };

Array index has eight elements, and array offset is a 4x2 array.

5.4.4. Initializers

Declared variables may specify an initial value using a syntax similar to C/C++, where the variable name is followed by an equals sign and the initial value or values for the variable. A scalar takes a single value, while vectors and arrays take nested lists of values inside of curly braces (the nesting matches the dimensionality of the declaration).

As in C, array initializers may be incomplete, i.e., the number of initializer elements may be less than the extent of the corresponding array dimension, with remaining array locations initialized to the default value for the specified array type.

Examples

      .const  .f32 vals[8] = { 0.33, 0.25, 0.125 };
      .global .s32 x[3][2] = { {1,2}, {3} };
is equivalent to 
      .const  .f32 vals[4] = { 0.33, 0.25, 0.125, 0.0, 0.0 };
      .global .s32 x[3][2] = { {1,2}, {3,0}, {0,0} };

Currently, variable initialization is supported only for constant and global state spaces. Variables in constant and global state spaces with no explicit initializer are initialized to zero by default. Initializers are not allowed in external variable declarations.

Variable names appearing in initializers represent the address of the variable; this can be used to statically initialize a pointer to a variable. Initializers may also contain var+offset expressions, where offset is a byte offset added to the address of var. Only variables in .global or .const state spaces may be used in initializers. By default, the resulting address is the offset in the variable's state space (as is the case when taking the address of a variable with a mov instruction). An operator, generic(), is provided to create a generic address for variables used in initializers.

Examples

      .const  .u32 foo = 42;
      .global .u32 bar[] = { 2, 3, 5 };
      .global .u32 p1 = foo;          // offset of foo in .const space
      .global .u32 p2 = generic(foo); // generic address of foo

      // array of generic-address pointers to elements of bar
      .global .u32 parr[] = { generic(bar), generic(bar)+4,
      generic(bar)+8 };
Note: PTX 3.1 redefines the default addressing for global variables in initializers, from generic addresses to offsets in the global state space. Legacy PTX code is treated as having an implicit generic() operator for each global variable used in an initializer. PTX 3.1 code should either include explicit generic() operators in initializers, use cvta.global to form generic addresses at runtime, or load from the non-generic address using ld.global.

Device function names appearing in initializers represent the address of the first instruction in the function; this can be used to initialize a table of function pointers to be used with indirect calls. Beginning in PTX ISA version 3.1, kernel function names can be used as initializers e.g. to initialize a table of kernel function pointers, to be used with CUDA Dynamic Parallelism to launch kernels from GPU. See the CUDA Dynamic Parallelism Programming Guide for details.

Labels cannot be used in initializers.

Variables that hold addresses of variables or functions should be of type .u32 or .u64.

Initializers are allowed for all types except .f16, .f16x2 and .pred.

Examples

      .global .s32 n = 10;
      .global .f32 blur_kernel[][3]
                     = {{.05,.1,.05},{.1,.4,.1},{.05,.1,.05}};

      .global .u32 foo[] = { 2, 3, 5, 7, 9, 11 };
      .global .u64 ptr = generic(foo);   // generic address of foo[0]
      .global .u64 ptr = generic(foo)+8; // generic address of foo[2]

5.4.5. Alignment

Byte alignment of storage for all addressable variables can be specified in the variable declaration. Alignment is specified using an optional .alignbyte-count specifier immediately following the state-space specifier. The variable will be aligned to an address which is an integer multiple of byte-count. The alignment value byte-count must be a power of two. For arrays, alignment specifies the address alignment for the starting address of the entire array, not for individual elements.

The default alignment for scalar and array variables is to a multiple of the base-type size. The default alignment for vector variables is to a multiple of the overall vector size.

Examples

       // allocate array at 4-byte aligned address.  Elements are bytes.
      .const .align 4 .b8 bar[8] = {0,0,0,0,2,0,0,0};

Note that all PTX instructions that access memory require that the address be aligned to a multiple of the transfer size.

5.4.6. Parameterized Variable Names

Since PTX supports virtual registers, it is quite common for a compiler frontend to generate a large number of register names. Rather than require explicit declaration of every name, PTX supports a syntax for creating a set of variables having a common prefix string appended with integer suffixes.

For example, suppose a program uses a large number, say one hundred, of .b32 variables, named %r0, %r1, ..., %r99. These 100 register variables can be declared as follows: 
      .reg .b32 %r<100>;    // declare %r0, %r1, ..., %r99

This shorthand syntax may be used with any of the fundamental types and with any state space, and may be preceded by an alignment specifier. Array variables cannot be declared this way, nor are initializers permitted.

5.4.7. Variable Attributes

Variables may be declared with an optional .attribute directive which allows specifying special attributes of variables. Keyword .attribute is followed by attribute specification inside parenthesis. Multiple attributes are separated by comma.

Variable Attribute Directive: .attribute describes the .attribute directive.

5.4.8. Variable Attribute Directive: .attribute

.attribute

Variable attributes

Description

Used to specify special attributes of a variable.

Following attributes are supported.

.managed
.managed attribute specifies that variable will be allocated at a location in unified virtual memory environment where host and other devices in the system can reference the variable directly. This attribute can only be used with variables in .global state space. See the CUDA UVM-Lite Programming Guide for details.

PTX ISA Notes

  • Introduced in PTX ISA version 4.0.

Target ISA Notes

  • .managed attribute requires sm_30 or higher.

Examples

     .global .attribute(.managed) .s32 g;
     .global .attribute(.managed) .u64 x;

6. Instruction Operands

6.1. Operand Type Information

All operands in instructions have a known type from their declarations. Each operand type must be compatible with the type determined by the instruction template and instruction type. There is no automatic conversion between types.

The bit-size type is compatible with every type having the same size. Integer types of a common size are compatible with each other. Operands having type different from but compatible with the instruction type are silently cast to the instruction type.

6.2. Source Operands

The source operands are denoted in the instruction descriptions by the names a, b, and c. PTX describes a load-store machine, so operands for ALU instructions must all be in variables declared in the .reg register state space. For most operations, the sizes of the operands must be consistent.

The cvt (convert) instruction takes a variety of operand types and sizes, as its job is to convert from nearly any data type to any other data type (and size).

The ld, st, mov, and cvt instructions copy data from one location to another. Instructions ld and st move data from/to addressable state spaces to/from registers. The mov instruction copies data between registers.

Most instructions have an optional predicate guard that controls conditional execution, and a few instructions have additional predicate source operands. Predicate operands are denoted by the names p, q, r, s.

6.3. Destination Operands

PTX instructions that produce a single result store the result in the field denoted by d (for destination) in the instruction descriptions. The result operand is a scalar or vector variable in the register state space.

6.4. Using Addresses, Arrays, and Vectors

Using scalar variables as operands is straightforward. The interesting capabilities begin with addresses, arrays, and vectors.

6.4.1. Addresses as Operands

All the memory instructions take an address operand that specifies the memory location being accessed. This addressable operand is one of:

[var]
the name of an addressable variable var
[reg]
an integer or bit-size type register reg containing a byte address
[reg+immOff]
a sum of register reg containing a byte address plus a constant integer byte offset (signed, 32-bit)
[var+immOff]
a sum of address of addresstable variable var containing a byte address plus a constant integer byte offset (signed, 32-bit)
[immAddr]
an immediate absolute byte address (unsigned, 32-bit)

The register containing an address may be declared as a bit-size type or integer type.

The address must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined. For example, among other things, the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.

The address size may be either 32-bit or 64-bit. Addresses are zero-extended to the specified width as needed, and truncated if the register width exceeds the state space address width for the target architecture.

Address arithmetic is performed using integer arithmetic and logical instructions. Examples include pointer arithmetic and pointer comparisons. All addresses and address computations are byte-based; there is no support for C-style pointer arithmetic.

The mov instruction can be used to move the address of a variable into a pointer. The address is an offset in the state space in which the variable is declared. Load and store operations move data between registers and locations in addressable state spaces. The syntax is similar to that used in many assembly languages, where scalar variables are simply named and addresses are de-referenced by enclosing the address expression in square brackets. Address expressions include variable names, address registers, address register plus byte offset, and immediate address expressions which evaluate at compile-time to a constant address.

Here are a few examples:

      .shared .u16 x;
      .reg    .u16 r0;
      .global .v4 .f32 V;
      .reg    .v4 .f32 W;
      .const  .s32 tbl[256];
      .reg    .b32 p;
      .reg    .s32 q;

      ld.shared.u16   r0,[x];
      ld.global.v4.f32 W, [V];
      ld.const.s32    q, [tbl+12];
      mov.u32         p, tbl;

6.4.1.1. Generic Addressing

If a memory instruction does not specify a state space, the operation is performed using generic addressing. The state spaces const, local and shared are modeled as windows within the generic address space. Each window is defined by a window base and a window size that is equal to the size of the corresponding state space. A generic address maps to global memory unless it falls within the window for const, local, or shared memory. Within each window, a generic address maps to an address in the underlying state space by subtracting the window base from the generic address.

6.4.2. Arrays as Operands

Arrays of all types can be declared, and the identifier becomes an address constant in the space where the array is declared. The size of the array is a constant in the program.

Array elements can be accessed using an explicitly calculated byte address, or by indexing into the array using square-bracket notation. The expression within square brackets is either a constant integer, a register variable, or a simple register with constant offset expression, where the offset is a constant expression that is either added or subtracted from a register variable. If more complicated indexing is desired, it must be written as an address calculation prior to use. Examples are: 

      ld.global.u32  s, a[0];
      ld.global.u32  s, a[N-1];
      mov.u32        s, a[1];  // move address of a[1] into s

6.4.3. Vectors as Operands

Vector operands are supported by a limited subset of instructions, which include mov, ld, st, and tex. Vectors may also be passed as arguments to called functions.

Vector elements can be extracted from the vector with the suffixes .x, .y, .z and .w, as well as the typical color fields .r, .g, .b and .a.

A brace-enclosed list is used for pattern matching to pull apart vectors.

      .reg .v4 .f32 V;
      .reg .f32     a, b, c, d;

      mov.v4.f32 {a,b,c,d}, V;

Vector loads and stores can be used to implement wide loads and stores, which may improve memory performance. The registers in the load/store operations can be a vector, or a brace-enclosed list of similarly typed scalars. Here are examples: 

      ld.global.v4.f32  {a,b,c,d}, [addr+16];
      ld.global.v2.u32  V2, [addr+8];

Elements in a brace-enclosed vector, say {Ra, Rb, Rc, Rd}, correspond to extracted elements as follows:

      Ra = V.x = V.r
      Rb = V.y = V.g
      Rc = V.z = V.b
      Rd = V.w = V.a

6.4.4. Labels and Function Names as Operands

Labels and function names can be used only in branch and call instructions respectively. Function names can be used in mov instruction to get the address of the function into a register, for use in an indirect call.

Beginning in PTX ISA version 3.1, the mov instruction may be used to take the address of kernel functions, to be passed to a system call that initiates a kernel launch from the GPU. This feature is part of the support for CUDA Dynamic Parallelism. See the CUDA Dynamic Parallelism Programming Guide for details.

6.5. Type Conversion

All operands to all arithmetic, logic, and data movement instruction must be of the same type and size, except for operations where changing the size and/or type is part of the definition of the instruction. Operands of different sizes or types must be converted prior to the operation.

6.5.1. Scalar Conversions

Table 13 shows what precision and format the cvt instruction uses given operands of differing types. For example, if a cvt.s32.u16 instruction is given a u16 source operand and s32 as a destination operand, the u16 is zero-extended to s32.

Conversions to floating-point that are beyond the range of floating-point numbers are represented with the maximum floating-point value (IEEE 754 Inf for f32 and f64, and ~131,000 for f16).

Table 13. Convert Instruction Precision and Format
  Destination Format
s8 s16 s32 s64 u8 u16 u32 u64 f16 f32 f64
Source Format
s8 - sext sext sext - sext sext sext s2f s2f s2f
s16 chop1 - sext sext chop1 - sext sext s2f s2f s2f
s32 chop1 chop1 - sext chop1 chop1 - sext s2f s2f s2f
s64 chop1 chop1 chop - chop1 chop1 chop - s2f s2f s2f
u8 - zext zext zext - zext zext zext u2f u2f u2f
u16 chop1 - zext zext chop1 - zext zext u2f u2f u2f
u32 chop1 chop1 - zext chop1 chop1 - zext u2f u2f u2f
u64 chop1 chop1 chop - chop1 chop1 chop - u2f u2f u2f
f16 f2s f2s f2s f2s f2u f2u f2u f2u - f2f f2f
f32 f2s f2s f2s f2s f2u f2u f2u f2u f2f - f2f
f64 f2s f2s f2s f2s f2u f2u f2u f2u f2f f2f -
Notes

sext = sign-extend; zext = zero-extend; chop = keep only low bits that fit;

s2f = signed-to-float; f2s = float-to-signed; u2f = unsigned-to-float;

f2u = float-to-unsigned; f2f = float-to-float.

1 If the destination register is wider than the destination format, the result is extended to the destination register width after chopping. The type of extension (sign or zero) is based on the destination format. For example, cvt.s16.u32 targeting a 32-bit register first chops to 16-bit, then sign-extends to 32-bit.

6.5.2. Rounding Modifiers

Conversion instructions may specify a rounding modifier. In PTX, there are four integer rounding modifiers and four floating-point rounding modifiers. Table 14 and Table 15 summarize the rounding modifiers.

Table 14. Floating-Point Rounding Modifiers
Modifier Description
.rn mantissa LSB rounds to nearest even
.rz mantissa LSB rounds towards zero
.rm mantissa LSB rounds towards negative infinity
.rp mantissa LSB rounds towards positive infinity
Table 15. Integer Rounding Modifiers
Modifier Description
.rni round to nearest integer, choosing even integer if source is equidistant between two integers.
.rzi round to nearest integer in the direction of zero
.rmi round to nearest integer in direction of negative infinity
.rpi round to nearest integer in direction of positive infinity

6.6. Operand Costs

Operands from different state spaces affect the speed of an operation. Registers are fastest, while global memory is slowest. Much of the delay to memory can be hidden in a number of ways. The first is to have multiple threads of execution so that the hardware can issue a memory operation and then switch to other execution. Another way to hide latency is to issue the load instructions as early as possible, as execution is not blocked until the desired result is used in a subsequent (in time) instruction. The register in a store operation is available much more quickly. Table 16 gives estimates of the costs of using different kinds of memory.

Table 16. Cost Estimates for Accessing State-Spaces
Space Time Notes
Register 0  
Shared 0  
Constant 0 Amortized cost is low, first access is high
Local > 100 clocks  
Parameter 0  
Immediate 0  
Global > 100 clocks  
Texture > 100 clocks  
Surface > 100 clocks  

7. Abstracting the ABI

Rather than expose details of a particular calling convention, stack layout, and Application Binary Interface (ABI), PTX provides a slightly higher-level abstraction and supports multiple ABI implementations. In this section, we describe the features of PTX needed to achieve this hiding of the ABI. These include syntax for function definitions, function calls, parameter passing, support for variadic functions (varargs), and memory allocated on the stack (alloca).

7.1. Function Declarations and Definitions

In PTX, functions are declared and defined using the .func directive. A function declaration specifies an optional list of return parameters, the function name, and an optional list of input parameters; together these specify the function's interface, or prototype. A function definition specifies both the interface and the body of the function. A function must be declared or defined prior to being called.

The simplest function has no parameters or return values, and is represented in PTX as follows: 

.func foo
{
    ...
    ret;
}

    ...
    call foo;
    ...

Here, execution of the call instruction transfers control to foo, implicitly saving the return address. Execution of the ret instruction within foo transfers control to the instruction following the call.

Scalar and vector base-type input and return parameters may be represented simply as register variables. At the call, arguments may be register variables or constants, and return values may be placed directly into register variables. The arguments and return variables at the call must have type and size that match the callee's corresponding formal parameters.

Example

.func (.reg .u32 %res) inc_ptr ( .reg .u32 %ptr, .reg .u32 %inc )
{
    add.u32 %res, %ptr, %inc;
    ret;
}

    ...
    call (%r1), inc_ptr, (%r1,4);
    ...

When using the ABI, .reg state space parameters must be at least 32-bits in size. Subword scalar objects in the source language should be promoted to 32-bit registers in PTX, or use .param state space byte arrays described next.

Objects such as C structures and unions are flattened into registers or byte arrays in PTX and are represented using .param space memory. For example, consider the following C structure, passed by value to a function: 
struct {
    double dbl;
    char   c[4];
};

In PTX, this structure will be flattened into a byte array. Since memory accesses are required to be aligned to a multiple of the access size, the structure in this example will be a 12 byte array with 8 byte alignment so that accesses to the .f64 field are aligned. The .param state space is used to pass the structure by value:

Example

.func (.reg .s32 out) bar (.reg .s32 x, .param .align 8 .b8 y[12])
{
    .reg .f64 f1;
    .reg .b32 c1, c2, c3, c4;
    ...
    ld.param.f64 f1, [y+0];
    ld.param.b8  c1, [y+8];
    ld.param.b8  c2, [y+9];
    ld.param.b8  c3, [y+10];
    ld.param.b8  c4, [y+11];
    ...
    ... // computation using x,f1,c1,c2,c3,c4;
}

{
     .param .b8 .align 8 py[12];
     ...
     st.param.b64 [py+ 0], %rd;
     st.param.b8  [py+ 8], %rc1;
     st.param.b8  [py+ 9], %rc2;
     st.param.b8  [py+10], %rc1;
     st.param.b8  [py+11], %rc2;
     // scalar args in .reg space, byte array in .param space
     call (%out), bar, (%x, py);
     ...

In this example, note that .param space variables are used in two ways. First, a .param variable y is used in function definition bar to represent a formal parameter. Second, a .param variable py is declared in the body of the calling function and used to set up the structure being passed to bar.

The following is a conceptual way to think about the .param state space use in device functions.

For a caller,
  • The .param state space is used to set values that will passed to a called function and/or to receive return values from a called function. Typically, a .param byte array is used to collect together fields of a structure being passed by value.
For a callee,
  • The .param state space is used to receive parameter values and/or pass return values back to the caller.

The following restrictions apply to parameter passing.

For a caller,
  • Arguments may be .param variables, .reg variables, or constants.
  • In the case of .param space formal parameters that are byte arrays, the argument must also be a .param space byte array with matching type, size, and alignment. A .param argument must be declared within the local scope of the caller.
  • In the case of .param space formal parameters that are base-type scalar or vector variables, the corresponding argument may be either a .param or .reg space variable with matching type and size, or a constant that can be represented in the type of the formal parameter.
  • In the case of .reg space formal parameters, the corresponding argument may be either a .param or .reg space variable of matching type and size, or a constant that can be represented in the type of the formal parameter.
  • In the case of .reg space formal parameters, the register must be at least 32-bits in size.
  • All st.param instructions used for passing arguments to function call must immediately precede the corresponding call instruction and ld.param instruction used for collecting return value must immediately follow the call instruction without any control flow alteration. st.param and ld.param instructions used for argument passing cannot be predicated. This enables compiler optimization and ensures that the .param variable does not consume extra space in the caller's frame beyond that needed by the ABI. The .param variable simply allows a mapping to be made at the call site between data that may be in multiple locations (e.g., structure being manipulated by caller is located in registers and memory) to something that can be passed as a parameter or return value to the callee.
For a callee,
  • Input and return parameters may be .param variables or .reg variables.
  • Parameters in .param memory must be aligned to a multiple of 1, 2, 4, 8, or 16 bytes.
  • Parameters in the .reg state space must be at least 32-bits in size.
  • The .reg state space can be used to receive and return base-type scalar and vector values, including sub-word size objects when compiling in non-ABI mode. Supporting the .reg state space provides legacy support.

Note that the choice of .reg or .param state space for parameter passing has no impact on whether the parameter is ultimately passed in physical registers or on the stack. The mapping of parameters to physical registers and stack locations depends on the ABI definition and the order, size, and alignment of parameters.

7.1.1. Changes from PTX ISA Version 1.x

In PTX ISA version 1.x, formal parameters were restricted to .reg state space, and there was no support for array parameters. Objects such as C structures were flattened and passed or returned using multiple registers. PTX ISA version 1.x supports multiple return values for this purpose.

Beginning with PTX ISA version 2.0, formal parameters may be in either .reg or .param state space, and .param space parameters support arrays. For targets sm_20 or higher, PTX restricts functions to a single return value, and a .param byte array should be used to return objects that do not fit into a register. PTX continues to support multiple return registers for sm_1x targets.

Note: PTX implements a stack-based ABI only for targets sm_20 or higher.

PTX ISA versions prior to 3.0 permitted variables in .reg and .local state spaces to be defined at module scope. When compiling to use the ABI, PTX ISA version 3.0 and later disallows module-scoped .reg and .local variables and restricts their use to within function scope. When compiling without use of the ABI, module-scoped .reg and .local variables are supported as before. When compiling legacy PTX code (ISA versions prior to 3.0) containing module-scoped .reg or .local variables, the compiler silently disables use of the ABI.

7.2. Variadic Functions

Note:Support for variadic functions which was unimplemented has been removed from the spec.

PTX version 6.0 supports passing unsized array parameter to a function which can be used to implement variadic functions.

Refer to Kernel and Function Directives: .func for details

7.3. Alloca

Note:The current version of PTX does not support alloca.
PTX provides another built-in function for allocating storage at runtime on the per-thread local memory stack. To allocate memory, a function simply calls the built-in function %alloca, defined as follows: 
.func ( .reg .u32 ptr ) %alloca ( .reg .u32 size );

The resulting pointer is to the base address in local memory of the allocated memory. The array is then accessed with ld.local and st.local instructions.

If a particular alignment is required, it is the responsibility of the user program to allocate additional space and adjust the base pointer to achieve the desired alignment. The built-in %alloca function is guaranteed only to return a 4-byte aligned pointer.

8. Memory Consistency Model

In multi-threaded executions, the side-effects of memory operations performed by each thread become visible to other threads in a partial and non-identical order. This means that any two operations may appear to happen in no order, or in different orders, to different threads. The axioms introduced by the memory consistency model specify exactly which contradictions are forbidden between the orders observed by different threads.

In the absence of any constraint, each read operation returns the value committed by some write operation to the same memory location, including the initial write to that memory location. The memory consistency model effectively constrains the set of such candidate writes from which a read operation can return a value.

Scope and applicability of the model

The constraints specified under this model apply to PTX programs with any PTX ISA version number, running on sm_70 or later architectures.

The memory consistency model does not apply to texture and surface accesses.

Limitations on atomicity at system scope

When communicating with the host CPU, the 64-bit strong operations with system scope may not be performed atomically on some systems. For more details on atomicity guarantees to host memory, see the CUDA Programming Guide.

8.2. Memory operations

The fundamental storage unit in the PTX memory model is a byte, consisting of 8 bits. Each state space available to a PTX program is a sequence of contiguous bytes in memory. Every byte in a PTX state space has a unique address relative to all threads that have access to the same state space.

Each PTX memory instruction specifies a memory address and a data-type. The memory address and the data-type together define a memory location, which is the range of bytes starting from the address and extended upto the size of the data-type in bytes.

Each PTX memory instruction also specifies the operation --- either a read, a write or an atomic read-modify-write --- to be performed on all the bytes in the corresponding memory location.

8.2.1. Overlap

Two memory locations are said to overlap when the starting address of one location is within the range of bytes constituting the other location. Two memory operations are said to overlap when the corresponding memory locations overlap. The overlap is said to be complete when both memory locations are identical, and it is said to be partial otherwise.

8.2.2. Vector Data-types

The memory consistency model relates operations executed on memory locations with scalar data-types, which have a maximum size and alignment of 64 bits. Memory operations with a vector data-type are modelled as a set of equivalent memory operations with a scalar data-type, executed in an unspecified order on the elements in the vector.

8.2.3. Initialization

Each byte in memory is initialized by a hypothetical write W0 executed before starting any thread in the program. If the byte is included in a program variable, and that variable has an initial value, then W0 writes the corresponding initial value for that byte; else W0 is assumed to have written an unknown but constant value to the byte.

8.3. State spaces

The relations defined in the memory consistency model are independent of state spaces. In particular, causality order closes over all memory operations across all the state spaces. But the side-effect of a memory operation in one state space can be observed directly only by operations that also have access to the same state space. This further constrains the synchronizing effect of a memory operation in addition to scope. For example, the synchronizing effect of the PTX instruction ld.relaxed.shared.sys is identical to that of ld.relaxed.shared.cta, since no thread outside the same CTA can execute an operation that accesses the same memory location.

8.4. Operation types

For simplicity, the rest of the document refers to the following operation types, instead of mentioning specific instructions that give rise to them.

Table 17. Operation Types
Operation type Instruction/Operation
atomic operation atom or red instruction.
read operation All variants of ld instruction and atom instruction (but not red instruction).
write operation All variants of st instruction, and atomic operations if they result in a write.
memory operation A read or write operation.
volatile operation An instruction with .volatile qualifier.
acquire operation

A memory operation with .acquire or .acq_rel qualifier.

release operation A memory operation with .release or .acq_rel qualifier.
strong operation A memory operation with a .relaxed, .acquire, .release, .acq_rel or .volatile qualifier.
weak operation An ld or st instruction with a .weak qualifier.
fence fence.sc (including membar), fence.acq_rel
synchronizing operation A bar instruction, fence operation, release operation or acquire operation.

8.5. Scope

Each strong operation and fence must specify a scope, which is the set of threads that may interact directly with that operation and establish any of the relations described in the memory consistency model. There are three scopes:

Table 18. Scopes
Scope Description
.cta The set of all threads executing in the same CTA as the current thread.
.gpu The set of all threads in the current program executing on the same compute device as the current thread. This also includes other kernel grids invoked by the host program on the same compute device.
.sys The set of all threads in the current program, including all kernel grids invoked by the host program on all compute devices, and all threads constituting the host program itself.

Note that the warp is not a scope; the CTA is the smallest collection of threads that qualifies as a scope in the memory consistency model.

8.6. Morally strong operations

Two operations are said to be morally strong relative to each other if:

  1. They are related in program order, i.e, they are both executed by the same thread, or,
  2. Both operations are strong, each specifies a scope that includes the thread executing the other operation and both operations overlap completely.

Most (but not all) of the axioms in the memory consistency model depend on relations between morally strong operations.

8.6.1. Conflict and Data-races

Two overlapping memory operations are said to conflict when at least one of them is a write.

Two conflicting memory operations are said to be in a data-race if they are not related in causality order and they are not morally strong.

8.6.2. Limitations on Mixed-size Data-races

A data-race between operations that overlap completely is called a uniform-size data-race, while a data-race between operations that overlap partially is called a mixed-size data-race.

The axioms in the memory consistency model do not apply if a PTX program contains one or more mixed-size data-races. But these axioms are sufficient to describe the behavior of a PTX program with only uniform-size data-races.

Atomicity of mixed-size RMW operations

In any program with or without mixed-size data-races, the following property holds for every pair of overlapping atomic operations A1 and A2 such that each specifies a scope that includes the other: Either the read-modify-write operation specified by A1 is performed completely before A2 is initiated, or vice versa. This property holds irrespective of whether the two operations A1 and A2 overlap partially or completely.

8.7. Release and Acquire Patterns

Some sequences of instructions give rise to patterns that participate in memory synchronization as described later. The release pattern makes prior operations from the current thread1 visible to some operations from other threads. The acquire pattern makes some operations from other threads visible to later operations from the current thread.

A release pattern on a location M consists of one of the following:

  1. A release operation on M

    E.g.: st.release [M]; or atom.acq_rel [M];

  2. Or a release operation on M followed by a strong write on M in program order

    E.g.: st.release [M]; st.relaxed [M];

  3. Or a fence followed by a strong write on M in program order

    E.g.: fence; st.relaxed [M];

Any memory synchronization established by a release pattern only affects operations occurring in program order before the first instruction in that pattern.

An acquire pattern on a location M consists of one of the following:

  1. An acquire operation on M

    E.g.: ld.acquire [M]; or atom.acq_rel [M];

  2. Or a strong read on M followed by an acquire operation on M in program order

    E.g.: ld.relaxed [M]; ld.acquire [M];

  3. Or a strong read on M followed by a fence in program order

    E.g.: ld.relaxed [M]; fence;

Any memory synchronization established by an acquire pattern only affects operations occurring in program order after the last instruction in that pattern.

1 For both release and acquire patterns, this effect is further extended to operations in other threads through the transitive nature of causality order.

8.8. Ordering of memory operations

The sequence of operations performed by each thread is captured as program order while memory synchronization across threads is captured as causality order. The visibility of the side-effects of memory operations to other memory operations is captured as communication order. The memory consistency model defines contradictions that are disallowed between communication order on the one hand, and causality order and program order on the other.

8.8.1. Program Order

The program order relates all operations performed by a thread to the order in which a sequential processor will execute instructions in the corresponding PTX source. It is a transitive relation that forms a total order over the operations performed by the thread, but does not relate operations from different threads.

8.8.2. Observation Order

Observation order relates a write W to a read R through an optional sequence of atomic read-modify-write operations.

A write W precedes a read R in observation order if:

  1. R and W are morally strong and R reads the value written by W, or
  2. For some atomic operation Z, W precedes Z and Z precedes R in observation order.

8.8.3. Fence-SC Order

The Fence-SC order is an acyclic partial order, determined at runtime, that relates every pair of morally strong fence.sc operations.

8.8.4. Memory synchronization

Synchronizing operations performed by different threads synchronize with each other at runtime as described here. The effect of such synchronization is to establish causality order across threads.

  1. A fence.sc operation X synchronizes with a fence.sc operation Y if X precedes Y in the Fence-SC order.
  2. A bar.sync or bar.red or bar.arrive operation synchronizes with a bar.sync or bar.red operation executed on the same barrier.
  3. A release pattern X synchronizes with an acquire pattern Y, if a write operation in X precedes a read operation in Y in observation order, and the first operation in X and the last operation in Y are morally strong.

8.8.5. Causality Order

Causality order captures how memory operations become visible across threads through synchronizing operations. The axiom “Causality” uses this order to constrain the set of write operations from which a read operation may read a value.

Relations in the causality order primarily consist of relations in Base causality order1 , which is a transitive order, determined at runtime.

Base causality order

An operation X precedes an operation Y in base causality order if:

  1. X synchronizes with Y, or
  2. For some operation Z,
    1. X precedes Z in program order and Z precedes Y in base causality order, or
    2. X precedes Z in base causality order and Z precedes Y in program order, or
    3. X precedes Z in base causality order and Z precedes Y in base causality order.

Causality order

Causality order combines base causality order with some non-transitive relations as follows:

An operation X precedes an operation Y in causality order if:

  1. X precedes Y in base causality order, or
  2. For some operation Z, X precedes Z in observation order, and:
    1. Z precedes Y in base causality order, or
    2. Z precedes Y in program order, and Z and Y overlap.

1 The transitivity of base causality order accounts for the “cumulativity” of synchronizing operations.

8.8.6. Coherence Order

There exists a partial transitive order that relates overlapping write operations, determined at runtime, called the coherence order1. Two overlapping write operations are related in coherence order if they are morally strong or if they are related in causality order. Two overlapping writes are unrelated in coherence order if they are in a data-race, which gives rise to the partial nature of coherence order.

1 Coherence order cannot be observed directly since it consists entirely of write operations. It may be observed indirectly by its use in constraining the set of candidate writes that a read operation may read from.

8.8.7. Communication Order

The communication order is a non-transitive order, determined at runtime, that relates write operations to other overlapping memory operations.

  1. A write W precedes an overlapping read R in communication order if R returns the value of any byte that was written by W.
  2. A write W precedes a write W’ in communication order if W precedes W’ in coherence order.
  3. A read R precedes an overlapping write W in communication order if, for any byte accessed by both R and W, R returns the value written by a write W’ that precedes W in coherence order.

Communication order captures the visibility of memory operations --- when a memory operation X1 precedes a memory operation X2 in communication order, X1 is said to be visible to X2.

8.9. Axioms

8.9.1. Coherence

If a write W precedes an overlapping write W’ in causality order, then W must precede W’ in coherence order.

8.9.2. Fence-SC

Fence-SC order cannot contradict causality order. For a pair of morally strong fence.sc operations F1 and F2, if F1 precedes F2 in causality order, then F1 must precede F2 in Fence-SC order.

8.9.3. Atomicity

Single-Copy Atomicity

Conflicting morally strong operations are performed with single-copy atomicity. When a read R and a write W are morally strong, then the following two communications cannot both exist in the same execution, for the set of bytes accessed by both R and W:

  1. R reads any byte from W.
  2. R reads any byte from any write W’ which precedes W in coherence order.

Atomicity of read-modify-write (RMW) operations

When an atomic operation A and a write W overlap and are morally strong, then the following two communications cannot both exist in the same execution, for the set of bytes accessed by both A and W:

  1. A reads any byte from a write W’ that precedes W in coherence order.
  2. A follows W in coherence order.

8.9.4. No Thin Air

Values may not appear "out of thin air": an execution cannot speculatively produce a value in such a way that the speculation becomes self-satisfying through chains of instruction dependencies and inter-thread communication. This matches both programmer intuition and hardware reality, but is necessary to state explicitly when performing formal analysis.

Litmus Test: Load Buffering

.global .u32 x = 0;
.global .u32 y = 0;
T1 T2 
A2: ld.global.u32 %r0, [x];
B2: st.global.u32 [y], %r0;
 
A2: ld.global.u32 %r1, [x];
B2: st.global.u32 [x], %r1;
 
FINAL STATE: x == 0 AND y == 0

The litmus test known as "LB" (Load Buffering) checks such forbidden values that may arise out of thin air. Two threads T1 and T2 each read from a first variable and copy the observed result into a second variable, with the first and second variable exchanged between the threads. If each variable is initially zero, the final result shall also be zero. If A1 reads from B2 and A2 reads from B1, then values passing through the memory operations in this example form a cycle: A1->B1->A2->B2->A1. Only the values x == 0 and y == 0 are allowed to satisfy this cycle. If any of the memory operations in this example were to speculatively associate a different value with the corresponding memory location, then such a speculation would become self-fulfilling, and hence forbidden.

8.9.5. Sequential Consistency Per Location

Within any set of overlapping memory operations that are pairwise morally strong, communication order cannot contradict program order, i.e., a concatenation of program order between overlapping operations and morally strong relations in communication order cannot result in a cycle. This ensures that each program slice of overlapping pairwise morally strong operations is strictly sequentially-consistent.

Litmus Test: CoRR

.global .u32 x = 0;
T1 T2 
W1: st.global.relaxed.sys.u32 [x], 1;
 
R1: ld.global.relaxed.u32 %r0, [x];
R2: ld.global.relaxed.u32 %r1, [x];
 
IF %r0 == 1 THEN %r1 == 1

The litmus test "CoRR" (Coherent Read-Read), demonstrates one consequence of this guarantee. A thread T1 executes a write W1 on a location x, and a thread T2 executes two (or an infinite sequence of) reads R1 and R2 on the same location x. No other writes are executed on x, except the one modelling the initial value. The operations W1, R1 and R2 are pairwise morally strong. If R1 reads from W1, then the subsequent read R2 must also observe the same value. If R2 observed the initial value of x instead, then this would form a sequence of morally-strong relations R2->W1->R1 in communication order that contradicts the program order R1->R2 in thread T2. Hence R2 cannot read the initial value of x in such an execution.

8.9.6. Causality

Relations in communication order cannot contradict causality order. This constrains the set of candidate write operations that a read operation may read from:

  1. If a read R precedes an overlapping write W in causality order, then R cannot read from W.
  2. If a write W precedes an overlapping read R in causality order, then for any byte accessed by both R and W, R cannot read from any write W’ that precedes W in coherence order.

Litmus Test: Message Passing

.global .u32 data = 0;
.global .u32 flag = 0;
T1 T2 
W1: st.global.u32 [data], 1;
F1: fence.sys;
W2: st.global.relaxed.sys.u32 [flag], 1;
 
R1: ld.global.relaxed.sys.u32 %r0, [flag];
F2: fence.sys;
R2: ld.global.u32 %r1, [data];
 
IF %r0 == 1 THEN %r1 == 1

The litmus test known as "MP" (Message Passing) represents the essence of typical synchronization algorithms. A vast majority of useful programs can be reduced to sequenced applications of this pattern.

Thread T1 first writes to a data variable and then to a flag variable while a second thread T2 first reads from the flag variable and then from the data variable. The operations on the flag are morally strong and the memory operations in each thread are separated by a fence, and these fences are morally strong.

If R1 observes W2, then the release pattern “F1; W2” synchronizes with the acquire pattern “R1; F2”. This establishes the causality order W1 -> F1 -> W2 -> R1 -> F2 -> R2. Then axiom causality guarantees that R2 cannot read from any write that precedes W1 in coherence order. In the absence of any other writes in this example, R2 must read from W1.

Litmus Test: Store Buffering

The litmus test known as "SB" (Store Buffering) demonstrates the sequential consistency enforced by the fence.sc. A thread T1 writes to a first variable, and then reads the value of a second variable, while a second thread T2 writes to the second variable and then reads the value of the first variable. The memory operations in each thread are separated by fence.sc instructions, and these fences are morally strong. 

.global .u32 x = 0;
.global .u32 y = 0;
T1 T2 
W1: st.global.u32 [x], 1;
F1: fence.sc.sys;
R1: ld.global.u32 %r0, [y];
 
W2: st.global.u32 [y], 1;
F2: fence.sc.sys;
R2: ld.global.u32 %r1, [x];
 
%r0 == 1 OR %r1 == 1

In any execution, either F1 precedes F2 in Fence-SC order, or vice versa. If F1 precedes F2 in Fence-SC order, then F1 synchronizes with F2. This establishes the causality order in W1 -> F1 -> F2 -> R2. Axiom causality ensures that R2 cannot read from any write that precedes W1 in coherence order. In the absence of any other write to that variable, R2 must read from W1. Similarly, in the case where F2 precedes F1 in Fence-SC order, R1 must read from W2. If each fence.sc in this example were replaced by a fence.acq_rel instruction, then this outcome is not guaranteed. There may be an execution where the write from each thread remains unobserved from the other thread, i.e., an execution is possible, where both R1 and R2 return the initial value “0” for variables y and x respectively.

9. Instruction Set

9.1. Format and Semantics of Instruction Descriptions

This section describes each PTX instruction. In addition to the name and the format of the instruction, the semantics are described, followed by some examples that attempt to show several possible instantiations of the instruction.

9.2. PTX Instructions

PTX instructions generally have from zero to four operands, plus an optional guard predicate appearing after an @ symbol to the left of the opcode:
  • @p opcode;
  • @p opcode a;
  • @p opcode d, a;
  • @p opcode d, a, b;
  • @p opcode d, a, b, c;

For instructions that create a result value, the d operand is the destination operand, while a, b, and c are source operands.

The setp instruction writes two destination registers. We use a | symbol to separate multiple destination registers. 

    setp.lt.s32  p|q, a, b;  // p = (a < b); q = !(a < b);

For some instructions the destination operand is optional. A bit bucket operand denoted with an underscore (_) may be used in place of a destination register.

9.3. Predicated Execution

In PTX, predicate registers are virtual and have .pred as the type specifier. So, predicate registers can be declared as 
      .reg .pred p, q, r;

All instructions have an optional guard predicate which controls conditional execution of the instruction. The syntax to specify conditional execution is to prefix an instruction with @{!}p, where p is a predicate variable, optionally negated. Instructions without a guard predicate are executed unconditionally.

Predicates are most commonly set as the result of a comparison performed by the setp instruction.

As an example, consider the high-level code 
      if (i < n)
          j = j + 1;
This can be written in PTX as 
      setp.lt.s32  p, i, n;    // p = (i < n)
@p    add.s32      j, j, 1;    // if i < n, add 1 to j
To get a conditional branch or conditional function call, use a predicate to control the execution of the branch or call instructions. To implement the above example as a true conditional branch, the following PTX instruction sequence might be used: 
      setp.lt.s32  p, i, n;    // compare i to n
@!p   bra  L1;                 // if False, branch over
      add.s32      j, j, 1;		
L1:  	...

9.3.1. Comparisons

9.3.1.1. Integer and Bit-Size Comparisons

The signed integer comparisons are the traditional eq (equal), ne (not-equal), lt (less-than), le (less-than-or-equal), gt (greater-than), and ge (greater-than-or-equal). The unsigned comparisons are eq, ne, lo (lower), ls (lower-or-same), hi (higher), and hs (higher-or-same). The bit-size comparisons are eq and ne; ordering comparisons are not defined for bit-size types.

Table 19 shows the operators for signed integer, unsigned integer, and bit-size types.

Table 19. Operators for Signed Integer, Unsigned Integer, and Bit-Size Types
Meaning Signed Operator Unsigned Operator Bit-Size Operator
a == b eq eq eq
a != b ne ne ne
a < b lt lo n/a
a <= b le ls n/a
a > b gt hi n/a
a >= b ge hs n/a

9.3.1.2. Floating Point Comparisons

The ordered floating-point comparisons are eq, ne, lt, le, gt, and ge. If either operand is NaN, the result is False. Table 20 lists the floating-point comparison operators.

Table 20. Floating-Point Comparison Operators
Meaning Floating-Point Operator
a == b && !isNaN(a) && !isNaN(b) eq
a != b && !isNaN(a) && !isNaN(b) ne
a < b && !isNaN(a) && !isNaN(b) lt
a <= b && !isNaN(a) && !isNaN(b) le
a > b && !isNaN(a) && !isNaN(b) gt
a >= b && !isNaN(a) && !isNaN(b) ge

To aid comparison operations in the presence of NaN values, unordered floating-point comparisons are provided: equ, neu, ltu, leu, gtu, and geu. If both operands are numeric values (not NaN), then the comparison has the same result as its ordered counterpart. If either operand is NaN, then the result of the comparison is True.

Table 21 lists the floating-point comparison operators accepting NaN values.

Table 21. Floating-Point Comparison Operators Accepting NaN
Meaning Floating-Point Operator
a == b || isNaN(a) || isNaN(b) equ
a != b || isNaN(a) || isNaN(b) neu
a < b || isNaN(a) || isNaN(b) ltu
a <= b || isNaN(a) || isNaN(b) leu
a > b || isNaN(a) || isNaN(b) gtu
a >= b || isNaN(a) || isNaN(b) geu

To test for NaN values, two operators num (numeric) and nan (isNaN) are provided. num returns True if both operands are numeric values (not NaN), and nan returns True if either operand is NaN. Table 22 lists the floating-point comparison operators testing for NaN values.

Table 22. Floating-Point Comparison Operators Testing for NaN
Meaning Floating-Point Operator
!isNaN(a) && !isNaN(b) num
isNaN(a) || isNaN(b) nan

9.3.2. Manipulating Predicates

Predicate values may be computed and manipulated using the following instructions: and, or, xor, not, and mov.

There is no direct conversion between predicates and integer values, and no direct way to load or store predicate register values. However, setp can be used to generate a predicate from an integer, and the predicate-based select (selp) instruction can be used to generate an integer value based on the value of a predicate; for example: 
      selp.u32 %r1,1,0,%p; 	// convert predicate to 32-bit value

9.4. Type Information for Instructions and Operands

Typed instructions must have a type-size modifier. For example, the add instruction requires type and size information to properly perform the addition operation (signed, unsigned, float, different sizes), and this information must be specified as a suffix to the opcode.

Example

      .reg .u16 d, a, b;

      add.u16 d, a, b;    // perform a 16-bit unsigned add

Some instructions require multiple type-size modifiers, most notably the data conversion instruction cvt. It requires separate type-size modifiers for the result and source, and these are placed in the same order as the operands. For example: 

      .reg .u16 a;
      .reg .f32 d;

      cvt.f32.u16 d, a;   // convert 16-bit unsigned to 32-bit float

In general, an operand's type must agree with the corresponding instruction-type modifier. The rules for operand and instruction type conformance are as follows:

  • Bit-size types agree with any type of the same size.
  • Signed and unsigned integer types agree provided they have the same size, and integer operands are silently cast to the instruction type if needed. For example, an unsigned integer operand used in a signed integer instruction will be treated as a signed integer by the instruction.
  • Floating-point types agree only if they have the same size; i.e., they must match exactly.

Table 23 summarizes these type checking rules.

Table 23. Type Checking Rules
  Operand Type
.bX .sX .uX .fX
Instruction Type
.bX okay okay okay okay
.sX okay okay okay invalid
.uX okay okay okay invalid
.fX okay invalid invalid okay
Note: Some operands have their type and size defined independently from the instruction type-size. For example, the shift amount operand for left and right shift instructions always has type .u32, while the remaining operands have their type and size determined by the instruction type.

Example

// 64-bit arithmetic right shift; shift amount 'b' is .u32
    shr.s64 d,a,b;

9.4.1. Operand Size Exceeding Instruction-Type Size

For convenience, ld, st, and cvt instructions permit source and destination data operands to be wider than the instruction-type size, so that narrow values may be loaded, stored, and converted using regular-width registers. For example, 8-bit or 16-bit values may be held directly in 32-bit or 64-bit registers when being loaded, stored, or converted to other types and sizes. The operand type checking rules are relaxed for bit-size and integer (signed and unsigned) instruction types; floating-point instruction types still require that the operand type-size matches exactly, unless the operand is of bit-size type.

When a source operand has a size that exceeds the instruction-type size, the source data is truncated (chopped) to the appropriate number of bits specified by the instruction type-size.

Table 24 summarizes the relaxed type-checking rules for source operands. Note that some combinations may still be invalid for a particular instruction; for example, the cvt instruction does not support .bX instruction types, so those rows are invalid for cvt.

Table 24. Relaxed Type-checking Rules for Source Operands
  Source Operand Type
b8 b16 b32 b64 s8 s16 s32 s64 u8 u16 u32 u64 f16 f32 f64
Instruction Type
b8 - chop chop chop - chop chop chop - chop chop chop chop chop chop
b16 inv - chop chop inv - chop chop inv - chop chop - chop chop
b32 inv inv - chop inv inv - chop inv inv - chop inv - chop
b64 inv inv inv - inv inv inv - inv inv inv - inv inv -
s8 - chop chop chop - chop chop chop - chop chop chop inv inv inv
s16 inv - chop chop inv - chop chop inv - chop chop inv inv inv
s32 inv inv - chop inv inv - chop inv inv - chop inv inv inv
s64 inv inv inv - inv inv inv - inv inv inv - inv inv inv
u8 - chop chop chop - chop chop chop - chop chop chop inv inv inv
u16 inv - chop chop inv - chop chop inv - chop chop inv inv inv
u32 inv inv - chop inv inv - chop inv inv - chop inv inv inv
u64 inv inv inv - inv inv inv - inv inv inv - inv inv inv
f16 inv - chop chop inv inv inv inv inv inv inv inv - inv inv
f32 inv inv - chop inv inv inv inv inv inv inv inv inv - inv
f64 inv inv inv - inv inv inv inv inv inv inv inv inv inv -
Notes

chop = keep only low bits that fit; "-" = allowed, but no conversion needed;

inv = invalid, parse error.

  1. Source register size must be of equal or greater size than the instruction-type size.
  2. Bit-size source registers may be used with any appropriately-sized instruction type. The data are truncated ("chopped") to the instruction-type size and interpreted according to the instruction type.
  3. Integer source registers may be used with any appropriately-sized bit-size or integer instruction type. The data are truncated to the instruction-type size and interpreted according to the instruction type.
  4. Floating-point source registers can only be used with bit-size or floating-point instruction types. When used with a narrower bit-size instruction type, the data are truncated. When used with a floating-point instruction type, the size must match exactly.

When a destination operand has a size that exceeds the instruction-type size, the destination data is zero- or sign-extended to the size of the destination register. If the corresponding instruction type is signed integer, the data is sign-extended; otherwise, the data is zero-extended.

Table 25 summarizes the relaxed type-checking rules for destination operands.

Table 25. Relaxed Type-checking Rules for Destination Operands
  Destination Operand Type
b8 b16 b32 b64 s8 s16 s32 s64 u8 u16 u32 u64 f16 f32 f64
Instruction Type
b8 - zext zext zext - zext zext zext - zext zext zext zext zext zext
b16 inv - zext zext inv - zext zext inv - zext zext - zext zext
b32 inv inv - zext inv inv - zext inv inv - zext inv - zext
b64 inv inv inv - inv inv inv - inv inv inv - inv inv -
s8 - sext sext sext - sext sext sext - sext sext sext inv inv inv
s16 inv - sext sext inv - sext sext inv - sext sext inv inv inv
s32 inv inv - sext inv inv - sext inv inv - sext inv inv inv
s64 inv inv inv - inv inv inv - inv inv inv - inv inv inv
u8 - zext zext zext - zext zext zext - zext zext zext inv inv inv
u16 inv - zext zext inv - zext zext inv - zext zext inv inv inv
u32 inv inv - zext inv inv - zext inv inv - zext inv inv inv
u64 inv inv inv - inv inv inv - inv inv inv - inv inv inv
f16 inv - zext zext inv inv inv inv inv inv inv inv - inv inv
f32 inv inv - zext inv inv inv inv inv inv inv inv inv - inv
f64 inv inv inv - inv inv inv inv inv inv inv inv inv inv -
Notes

sext = sign-extend; zext = zero-extend; "-" = allowed, but no conversion needed;

inv = invalid, parse error.

  1. Destination register size must be of equal or greater size than the instruction-type size.
  2. Bit-size destination registers may be used with any appropriately-sized instruction type. The data are sign-extended to the destination register width for signed integer instruction types, and are zero-extended to the destination register width otherwise.
  3. Integer destination registers may be used with any appropriately-sized bit-size or integer instruction type. The data are sign-extended to the destination register width for signed integer instruction types, and are zero-extended to the destination register width for bit-size an d unsigned integer instruction types.
  4. Floating-point destination registers can only be used with bit-size or floating-point instruction types. When used with a narrower bit-size instruction type, the data are zero-extended. When used with a floating-point instruction type, the size must match exactly.

9.5. Divergence of Threads in Control Constructs

Threads in a CTA execute together, at least in appearance, until they come to a conditional control construct such as a conditional branch, conditional function call, or conditional return. If threads execute down different control flow paths, the threads are called divergent. If all of the threads act in unison and follow a single control flow path, the threads are called uniform. Both situations occur often in programs.

A CTA with divergent threads may have lower performance than a CTA with uniformly executing threads, so it is important to have divergent threads re-converge as soon as possible. All control constructs are assumed to be divergent points unless the control-flow instruction is marked as uniform, using the .uni suffix. For divergent control flow, the optimizing code generator automatically determines points of re-convergence. Therefore, a compiler or code author targeting PTX can ignore the issue of divergent threads, but has the opportunity to improve performance by marking branch points as uniform when the compiler or author can guarantee that the branch point is non-divergent.

9.6. Semantics

The goal of the semantic description of an instruction is to describe the results in all cases in as simple language as possible. The semantics are described using C, until C is not expressive enough.

9.6.1. Machine-Specific Semantics of 16-bit Code

A PTX program may execute on a GPU with either a 16-bit or a 32-bit data path. When executing on a 32-bit data path, 16-bit registers in PTX are mapped to 32-bit physical registers, and 16-bit computations are promoted to 32-bit computations. This can lead to computational differences between code run on a 16-bit machine versus the same code run on a 32-bit machine, since the promoted computation may have bits in the high-order half-word of registers that are not present in 16-bit physical registers. These extra precision bits can become visible at the application level, for example, by a right-shift instruction.

At the PTX language level, one solution would be to define semantics for 16-bit code that is consistent with execution on a 16-bit data path. This approach introduces a performance penalty for 16-bit code executing on a 32-bit data path, since the translated code would require many additional masking instructions to suppress extra precision bits in the high-order half-word of 32-bit registers.

Rather than introduce a performance penalty for 16-bit code running on 32-bit GPUs, the semantics of 16-bit instructions in PTX is machine-specific. A compiler or programmer may chose to enforce portable, machine-independent 16-bit semantics by adding explicit conversions to 16-bit values at appropriate points in the program to guarantee portability of the code. However, for many performance-critical applications, this is not desirable, and for many applications the difference in execution is preferable to limiting performance.

9.7.9. Instructions

All PTX instructions may be predicated. In the following descriptions, the optional guard predicate is omitted from the syntax.

9.7.1. Integer Arithmetic Instructions

Integer arithmetic instructions operate on the integer types in register and constant immediate forms. The integer arithmetic instructions are:

  • add
  • sub
  • mul
  • mad
  • mul24
  • mad24
  • sad
  • div
  • rem
  • abs
  • neg
  • min
  • max
  • popc
  • clz
  • bfind
  • fns
  • brev
  • bfe
  • bfi
  • dp4a
  • dp2a

9.7.1.1. Integer Arithmetic Instructions: add

add

Add two values.

Syntax
add.type       d, a, b;
add{.sat}.s32  d, a, b;     // .sat applies only to .s32

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Performs addition and writes the resulting value into a destination register.

Semantics
d = a + b;
Notes
Saturation modifier:
.sat
limits result to MININT..MAXINT (no overflow) for the size of the operation. Applies only to .s32 type.
PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
@p  add.u32     x,y,z;
    add.sat.s32 c,c,1;

9.7.1.2. Integer Arithmetic Instructions: sub

sub

Subtract one value from another.

Syntax
sub.type       d, a, b;
sub{.sat}.s32  d, a, b;     // .sat applies only to .s32

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Performs subtraction and writes the resulting value into a destination register.

Semantics
d = a - b;
Notes
Saturation modifier:
.sat
limits result to MININT..MAXINT (no overflow) for the size of the operation. Applies only to .s32 type.
PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    sub.s32 c,a,b;

9.7.1.3. Integer Arithmetic Instructions: mul

mul

Multiply two values.

Syntax
mul{.hi,.lo,.wide}.type  d, a, b;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Compute the product of two values.

Semantics
t = a * b;
n = bitwidth of type;
d = t;            // for .wide 
d = t<2n-1..n>;   // for .hi variant
d = t<n-1..0>;    // for .lo variant
Notes

The type of the operation represents the types of the a and b operands. If .hi or .lo is specified, then d is the same size as a and b, and either the upper or lower half of the result is written to the destination register. If .wide is specified, then d is twice as wide as a and b to receive the full result of the multiplication.

The .wide suffix is supported only for 16- and 32-bit integer types.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    mul.wide.s16 fa,fxs,fys;   // 16*16 bits yields 32 bits
    mul.lo.s16 fa,fxs,fys;     // 16*16 bits, save only the low 16 bits
    mul.wide.s32 z,x,y;        // 32*32 bits, creates 64 bit result

9.7.1.4. Integer Arithmetic Instructions: mad

mad

Multiply two values, optionally extract the high or low half of the intermediate result, and add a third value.

Syntax
mad{.hi,.lo,.wide}.type  d, a, b, c;
mad.hi.sat.s32           d, a, b, c;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Multiplies two values, optionally extracts the high or low half of the intermediate result, and adds a third value. Writes the result into a destination register.

Semantics
t = a * b;
n = bitwidth of type;
d = t + c;           // for .wide
d = t<2n-1..n> + c;  // for .hi variant
d = t<n-1..0> + c;   // for .lo variant
Notes

The type of the operation represents the types of the a and b operands. If .hi or .lo is specified, then d and c are the same size as a and b, and either the upper or lower half of the result is written to the destination register. If .wide is specified, then d and c are twice as wide as a and b to receive the result of the multiplication.

The .wide suffix is supported only for 16-bit and 32-bit integer types.

Saturation modifier:

.sat

limits result to MININT..MAXINT (no overflow) for the size of the operation.

Applies only to .s32 type in .hi mode.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
@p  mad.lo.s32 d,a,b,c;
    mad.lo.s32 r,p,q,r;

9.7.1.5. Integer Arithmetic Instructions: mul24

mul24

Multiply two 24-bit integer values.

Syntax
mul24{.hi,.lo}.type  d, a, b;

.type = { .u32, .s32 };
Description

Compute the product of two 24-bit integer values held in 32-bit source registers, and return either the high or low 32-bits of the 48-bit result.

Semantics
t = a * b;
d = t<47..16>;    // for .hi variant
d = t<31..0>;     // for .lo variant
Notes

Integer multiplication yields a result that is twice the size of the input operands, i.e., 48-bits.

mul24.hi performs a 24x24-bit multiply and returns the high 32 bits of the 48-bit result.

mul24.lo performs a 24x24-bit multiply and returns the low 32 bits of the 48-bit result.

All operands are of the same type and size.

mul24.hi may be less efficient on machines without hardware support for 24-bit multiply.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    mul24.lo.s32 d,a,b;   // low 32-bits of 24x24-bit signed multiply.

9.7.1.6. Integer Arithmetic Instructions: mad24

mad24

Multiply two 24-bit integer values and add a third value.

Syntax
mad24{.hi,.lo}.type  d, a, b, c;
mad24.hi.sat.s32     d, a, b, c;

.type = { .u32, .s32 };
Description

Compute the product of two 24-bit integer values held in 32-bit source registers, and add a third, 32-bit value to either the high or low 32-bits of the 48-bit result. Return either the high or low 32-bits of the 48-bit result.

Semantics
t = a * b;
d = t<47..16> + c;   // for .hi variant
d = t<31..0> + c;    // for .lo variant
Notes

Integer multiplication yields a result that is twice the size of the input operands, i.e., 48-bits.

mad24.hi performs a 24x24-bit multiply and adds the high 32 bits of the 48-bit result to a third value.

mad24.lo performs a 24x24-bit multiply and adds the low 32 bits of the 48-bit result to a third value.

All operands are of the same type and size.

Saturation modifier:
.sat
limits result of 32-bit signed addition to MININT..MAXINT (no overflow). Applies only to .s32 type in .hi mode.

mad24.hi may be less efficient on machines without hardware support for 24-bit multiply.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
mad24.lo.s32 d,a,b,c;   // low 32-bits of 24x24-bit signed multiply.

9.7.1.7. Integer Arithmetic Instructions: sad

sad

Sum of absolute differences.

Syntax
sad.type  d, a, b, c;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Adds the absolute value of a-b to c and writes the resulting value into d.

Semantics
d = c + ((a<b) ? b-a : a-b);
PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    sad.s32  d,a,b,c;
    sad.u32  d,a,b,d;  // running sum

9.7.1.8. Integer Arithmetic Instructions: div

div

Divide one value by another.

Syntax
div.type  d, a, b;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Divides a by b, stores result in d.

Semantics
d = a / b;
Notes

Division by zero yields an unspecified, machine-specific value.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    div.s32  b,n,i;

9.7.1.9. Integer Arithmetic Instructions: rem

rem

The remainder of integer division.

Syntax
rem.type  d, a, b;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Divides a by b, store the remainder in d.

Semantics
d = a % b;
Notes

The behavior for negative numbers is machine-dependent and depends on whether divide rounds towards zero or negative infinity.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    rem.s32  x,x,8;    // x = x%8;

9.7.1.10. Integer Arithmetic Instructions: abs

abs

Absolute value.

Syntax
abs.type  d, a;

.type = { .s16, .s32, .s64 };
Description

Take the absolute value of a and store it in d.

Semantics
d = |a|;
Notes

Only for signed integers.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    abs.s32  r0,a;

9.7.1.11. Integer Arithmetic Instructions: neg

neg

Arithmetic negate.

Syntax
neg.type  d, a;

.type = { .s16, .s32, .s64 };
Description

Negate the sign of a and store the result in d.

Semantics
d = -a;
Notes

Only for signed integers.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    neg.s32  r0,a;

9.7.1.12. Integer Arithmetic Instructions: min

min

Find the minimum of two values.

Syntax
min.type  d, a, b;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Store the minimum of a and b in d.

Semantics
d = (a < b) ? a : b; // Integer (signed and unsigned)
Notes

Signed and unsigned differ.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    min.s32  r0,a,b;
@p  min.u16  h,i,j;

9.7.1.13. Integer Arithmetic Instructions: max

max

Find the maximum of two values.

Syntax
max.type  d, a, b;

.type = { .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Store the maximum of a and b in d.

Semantics
d = (a > b) ? a : b; // Integer (signed and unsigned)
Notes

Signed and unsigned differ.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    max.u32  d,a,b;
    max.s32  q,q,0;

9.7.1.14. Integer Arithmetic Instructions: popc

popc

Population count.

Syntax
popc.type  d, a;

.type = { .b32, .b64 };
Description

Count the number of one bits in a and place the resulting population count in 32-bit destination register d. Operand a has the instruction type and destination d has type .u32.

Semantics
.u32  d = 0;
while (a != 0) {
   if (a & 0x1)  d++;
   a = a >> 1;
}
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

popc requires sm_20 or higher.

Examples
    popc.b32  d, a;
    popc.b64  cnt, X;  // cnt is .u32

9.7.1.15. Integer Arithmetic Instructions: clz

clz

Count leading zeros.

Syntax
clz.type  d, a;

.type = { .b32, .b64 };
Description

Count the number of leading zeros in a starting with the most-significant bit and place the result in 32-bit destination register d. Operand a has the instruction type, and destination d has type .u32. For .b32 type, the number of leading zeros is between 0 and 32, inclusively. For.b64 type, the number of leading zeros is between 0 and 64, inclusively.

Semantics
.u32  d = 0;
if (.type == .b32)   { max = 32; mask = 0x80000000; }
else                 { max = 64; mask = 0x8000000000000000; }

while (d < max && (a&mask == 0) ) {
    d++;
    a = a << 1;
}
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

clz requires sm_20 or higher.

Examples
    clz.b32  d, a;
    clz.b64  cnt, X;  // cnt is .u32

9.7.1.16. Integer Arithmetic Instructions: bfind

bfind

Find most significant non-sign bit.

Syntax
bfind.type           d, a;
bfind.shiftamt.type  d, a;

.type = { .u32, .u64,
          .s32, .s64 };
Description

Find the bit position of the most significant non-sign bit in a and place the result in d. Operand a has the instruction type, and destination d has type .u32. For unsigned integers, bfind returns the bit position of the most significant 1. For signed integers, bfind returns the bit position of the most significant 0 for negative inputs and the most significant 1 for non-negative inputs.

If .shiftamt is specified, bfind returns the shift amount needed to left-shift the found bit into the most-significant bit position.

bfind returns 0xffffffff if no non-sign bit is found.

Semantics
msb = (.type==.u32 || .type==.s32) ? 31 : 63;
// negate negative signed inputs
if ( (.type==.s32 || .type==.s64) && (a & (1<<msb)) ) {
    a = ~a;
}
.u32  d = 0xffffffff;
for (.s32 i=msb; i>=0; i--) {
    if (a & (1<<i))  { d = i; break; }
}
if (.shiftamt && d != 0xffffffff)  { d = msb - d; }
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

bfind requires sm_20 or higher.

Examples
    bfind.u32  d, a;
    bfind.shiftamt.s64  cnt, X;  // cnt is .u32

9.7.1.17. Integer Arithmetic Instructions: fns

fns

Find the n-th set bit

Syntax
fns.b32 d, mask, base, offset;
Description

Given a 32-bit value mask and an integer value base (between 0 and 31), find the n-th (given by offset) set bit in mask from the base bit, and store the bit position in d. If not found, store 0xffffffff in d.

Operand mask has a 32-bit type. Operand base has .b32, .u32 or .s32 type. Operand offset has .s32 type. Destination d has type .b32.

Operand base must be <= 31, otherwise behavior is undefined.

Semantics
d = 0xffffffff;
if (offset == 0) {
    if (mask[base] == 1) {
        d = base;
    }
} else {
    pos = base;
    count = |offset| - 1;
    inc = (offset > 0) ? 1 : -1;

    while ((pos >= 0) && (pos < 32)) {
        if (mask[pos] == 1) {
            if (count == 0) {
              d = pos;
              break;
           } else {
               count = count – 1;
           }
        }
        pos = pos + inc;
    }
}
PTX ISA Notes

Introduced in PTX ISA version 6.0.

Target ISA Notes

fns requires sm_30 or higher.

Examples
    fns.b32 d, 0xaaaaaaaa, 3, 1;   // d = 3
    fns.b32 d, 0xaaaaaaaa, 3, -1;  // d = 3
    fns.b32 d, 0xaaaaaaaa, 2, 1;   // d = 3
    fns.b32 d, 0xaaaaaaaa, 2, -1;  // d = 1

9.7.1.18. Integer Arithmetic Instructions: brev

brev

Bit reverse.

Syntax
brev.type  d, a;

.type = { .b32, .b64 };
Description

Perform bitwise reversal of input.

Semantics
msb = (.type==.b32) ? 31 : 63;

for (i=0; i<=msb; i++) {
    d[i] = a[msb-i];
}
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

brev requires sm_20 or higher.

Examples
    brev.b32  d, a;

9.7.1.19. Integer Arithmetic Instructions: bfe

bfe

Bit Field Extract.

Syntax
bfe.type  d, a, b, c;

.type = { .u32, .u64,
          .s32, .s64 };
Description

Extract bit field from a and place the zero or sign-extended result in d. Source b gives the bit field starting bit position, and source c gives the bit field length in bits.

Operands a and d have the same type as the instruction type. Operands b and c are type .u32, but are restricted to the 8-bit value range 0..255.

The sign bit of the extracted field is defined as:
.u32, .u64:
zero
.s32, .s64:
msb of input a if the extracted field extends beyond the msb of a msb of extracted field, otherwise

If the bit field length is zero, the result is zero.

The destination d is padded with the sign bit of the extracted field. If the start position is beyond the msb of the input, the destination d is filled with the replicated sign bit of the extracted field.

Semantics
msb = (.type==.u32 || .type==.s32) ? 31 : 63;
pos = b & 0xff;  // pos restricted to 0..255 range
len = c & 0xff;  // len restricted to 0..255 range

if (.type==.u32 || .type==.u64 || len==0)
    sbit = 0;
else
    sbit = a[min(pos+len-1,msb)];

d = 0;
for (i=0; i<=msb; i++) {
    d[i] = (i<len && pos+i<=msb) ? a[pos+i] : sbit;
}
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

bfe requires sm_20 or higher.

Examples
    bfe.b32  d,a,start,len;

9.7.1.20. Integer Arithmetic Instructions: bfi

bfi

Bit Field Insert.

Syntax
bfi.type  f, a, b, c, d;

.type = { .b32, .b64 };
Description

Align and insert a bit field from a into b, and place the result in f. Source c gives the starting bit position for the insertion, and source d gives the bit field length in bits.

Operands a, b, and f have the same type as the instruction type. Operands c and d are type .u32, but are restricted to the 8-bit value range 0..255.

If the bit field length is zero, the result is b.

If the start position is beyond the msb of the input, the result is b.

Semantics
msb = (.type==.b32) ? 31 : 63;
pos = c & 0xff;  // pos restricted to 0..255 range
len = d & 0xff;  // len restricted to 0..255 range

f = b;
for (i=0; i<len && pos+i<=msb; i++) {
    f[pos+i] = a[i];
}
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

bfi requires sm_20 or higher.

Examples
    bfi.b32  d,a,b,start,len;

9.7.1.21. Integer Arithmetic Instructions: dp4a

dp4a

Four-way byte dot product-accumulate.

Syntax
dp4a.atype.btype  d, a, b, c;

.atype = .btype = { .u32, .s32 };
Description

Four-way byte dot product which is accumulated in 32-bit result.

Operand a and b are 32-bit inputs which hold 4 byte inputs in packed form for dot product.

Operand c has type .u32 if both .atype and .btype are .u32 else operand c has type .s32.

Semantics
d = c;

// Extract 4 bytes from a 32bit input and sign or zero extend
// based on input type.
Va = extractAndSignOrZeroExt_4(a, .atype);
Vb = extractAndSignOrZeroExt_4(b, .btype);

for (i = 0; i < 4; ++i) {
    d += Va[i] * Vb[i]; 
}
PTX ISA Notes

Introduced in PTX ISA version 5.0.

Target ISA Notes

Requires sm_61 or higher.

Examples
dp4a.u32.u32           d0, a0, b0, c0;
dp4a.u32.s32           d1, a1, b1, c1;

9.7.1.22. Integer Arithmetic Instructions: dp2a

dp2a

Two-way dot product-accumulate.

Syntax
dp2a.mode.atype.btype  d, a, b, c;

.atype = .btype = { .u32, .s32 };
.mode = { .lo, .hi };
Description

Two-way 16-bit to 8-bit dot product which is accumulated in 32-bit result.

Operand a and b are 32-bit inputs. Operand a holds two 16-bits inputs in packed form and operand b holds 4 byte inputs in packed form for dot product.

Depending on the .mode specified, either lower half or upper half of operand b will be used for dot product.

Operand c has type .u32 if both .atype and .btype are .u32 else operand c has type .s32.

Semantics
d = c;
// Extract two 16-bit values from a 32-bit input and sign or zero extend
// based on input type.
Va = extractAndSignOrZeroExt_2(a, .atype); 

// Extract four 8-bit values from a 32-bit input and sign or zer extend
// based on input type.
Vb = extractAndSignOrZeroExt_4(b, .btype);

b_select = (.mode == .lo) ? 0 : 2;

for (i = 0; i < 2; ++i) {
    d += Va[i] * Vb[b_select + i];
}
PTX ISA Notes

Introduced in PTX ISA version 5.0.

Target ISA Notes

Requires sm_61 or higher.

Examples
    dp2a.lo.u32.u32           d0, a0, b0, c0;
    dp2a.hi.u32.s32           d1, a1, b1, c1;

9.7.2. Extended-Precision Integer Arithmetic Instructions

Instructions add.cc, addc, sub.cc, subc, mad.cc and madc reference an implicitly specified condition code register (CC) having a single carry flag bit (CC.CF) holding carry-in/carry-out or borrow-in/borrow-out. These instructions support extended-precision integer addition, subtraction, and multiplication. No other instructions access the condition code, and there is no support for setting, clearing, or testing the condition code. The condition code register is not preserved across calls and is mainly intended for use in straight-line code sequences for computing extended-precision integer addition, subtraction, and multiplication.

The extended-precision arithmetic instructions are:
  • add.cc, addc
  • sub.cc, subc
  • mad.cc, madc

9.7.2.1. Extended-Precision Arithmetic Instructions: add.cc

add.cc

Add two values with carry-out.

Syntax
add.cc.type  d, a, b;

.type = { .u32, .s32, .u64, .s64 };
Description

Performs integer addition and writes the carry-out value into the condition code register.

Semantics
d = a + b;

carry-out written to CC.CF

Notes

No integer rounding modifiers.

No saturation.

Behavior is the same for unsigned and signed integers.

PTX ISA Notes

32-bit add.cc introduced in PTX ISA version 1.2.

64-bit add.cc introduced in PTX ISA version 4.3.

Target ISA Notes

32-bit add.cc is supported on all target architectures.

64-bit add.cc requires sm_20 or higher.

Examples
@p  add.cc.u32   x1,y1,z1;   // extended-precision addition of
@p  addc.cc.u32  x2,y2,z2;   // two 128-bit values
@p  addc.cc.u32  x3,y3,z3;
@p  addc.u32     x4,y4,z4;

9.7.2.2. Extended-Precision Arithmetic Instructions: addc

addc

Add two values with carry-in and optional carry-out.

Syntax
addc{.cc}.type  d, a, b;

.type = { .u32, .s32, .u64, .s64 };
Description

Performs integer addition with carry-in and optionally writes the carry-out value into the condition code register.

Semantics
d = a + b + CC.CF;

if .cc specified, carry-out written to CC.CF

Notes

No integer rounding modifiers.

No saturation.

Behavior is the same for unsigned and signed integers.

PTX ISA Notes

32-bit add.cc introduced in PTX ISA version 1.2.

64-bit add.cc introduced in PTX ISA version 4.3.

Target ISA Notes

32-bit add.cc is supported on all target architectures.

64-bit add.cc requires sm_20 or higher.

Examples
@p  add.cc.u32   x1,y1,z1;   // extended-precision addition of
@p  addc.cc.u32  x2,y2,z2;   // two 128-bit values
@p  addc.cc.u32  x3,y3,z3;
@p  addc.u32     x4,y4,z4;

9.7.2.3. Extended-Precision Arithmetic Instructions: sub.cc

sub.cc

Subtract one value from another, with borrow-out.

Syntax
sub.cc.type  d, a, b;

.type = { .u32, .s32, .u64, .s64 };
Description

Performs integer subtraction and writes the borrow-out value into the condition code register.

Semantics
d = a - b;

borrow-out written to CC.CF

Notes

No integer rounding modifiers.

No saturation.

Behavior is the same for unsigned and signed integers.

PTX ISA Notes

32-bit add.cc introduced in PTX ISA version 1.2.

64-bit add.cc introduced in PTX ISA version 4.3.

Target ISA Notes

32-bit add.cc is supported on all target architectures.

64-bit add.cc requires sm_20 or higher.

Examples
@p  sub.cc.u32   x1,y1,z1;   // extended-precision subtraction
@p  subc.cc.u32  x2,y2,z2;   // of two 128-bit values
@p  subc.cc.u32  x3,y3,z3;
@p  subc.u32     x4,y4,z4;

9.7.2.4. Extended-Precision Arithmetic Instructions: subc

subc

Subtract one value from another, with borrow-in and optional borrow-out.

Syntax
subc{.cc}.type  d, a, b;

.type = { .u32, .s32, .u64, .s64 };
Description

Performs integer subtraction with borrow-in and optionally writes the borrow-out value into the condition code register.

Semantics
d = a  - (b + CC.CF);

if .cc specified, borrow-out written to CC.CF

Notes

No integer rounding modifiers.

No saturation.

Behavior is the same for unsigned and signed integers.

PTX ISA Notes

32-bit add.cc introduced in PTX ISA version 1.2.

64-bit add.cc introduced in PTX ISA version 4.3.

Target ISA Notes

32-bit add.cc is supported on all target architectures.

64-bit add.cc requires sm_20 or higher.

Examples
@p  sub.cc.u32   x1,y1,z1;   // extended-precision subtraction
@p  subc.cc.u32  x2,y2,z2;   // of two 128-bit values
@p  subc.cc.u32  x3,y3,z3;
@p  subc.u32     x4,y4,z4;

9.7.2.5. Extended-Precision Arithmetic Instructions: mad.cc

mad.cc

Multiply two values, extract high or low half of result, and add a third value with carry-out.

Syntax
mad{.hi,.lo}.cc.type  d, a, b, c;

.type = { .u32, .s32, .u64, .s64 };
Description

Multiplies two values, extracts either the high or low part of the result, and adds a third value. Writes the result to the destination register and the carry-out from the addition into the condition code register.

Semantics
t = a * b;
d = t<63..32> + c;    // for .hi variant
d = t<31..0> + c;     // for .lo variant

carry-out from addition is written to CC.CF

Notes

Generally used in combination with madc and addc to implement extended-precision multi-word multiplication. See madc for an example.

PTX ISA Notes

32-bit mad.cc introduced in PTX ISA version 3.0.

64-bit mad.cc introduced in PTX ISA version 4.3.

Target ISA Notes

Requires target sm_20 or higher.

Examples
@p  mad.lo.cc.u32 d,a,b,c;
    mad.lo.cc.u32 r,p,q,r;

9.7.2.6. Extended-Precision Arithmetic Instructions: madc

madc

Multiply two values, extract high or low half of result, and add a third value with carry-in and optional carry-out.

Syntax
madc{.hi,.lo}{.cc}.type  d, a, b, c;

.type = { .u32, .s32, .u64, .s64 };
Description

Multiplies two values, extracts either the high or low part of the result, and adds a third value along with carry-in. Writes the result to the destination register and optionally writes the carry-out from the addition into the condition code register.

Semantics
t = a * b;
d = t<63..32> + c + CC.CF;     // for .hi variant
d = t<31..0> + c + CC.CF;      // for .lo variant

if .cc specified, carry-out from addition is written to CC.CF

Notes

Generally used in combination with mad.cc and addc to implement extended-precision multi-word multiplication. See example below.

PTX ISA Notes

32-bit mad.cc introduced in PTX ISA version 3.0.

64-bit mad.cc introduced in PTX ISA version 4.3.

Target ISA Notes

Requires target sm_20 or higher.

Examples
// extended-precision multiply:  [r3,r2,r1,r0] = [r5,r4] * [r7,r6]
mul.lo.u32     r0,r4,r6;      // r0=(r4*r6).[31:0], no carry-out
mul.hi.u32     r1,r4,r6;      // r1=(r4*r6).[63:32], no carry-out
mad.lo.cc.u32  r1,r5,r6,r1;   // r1+=(r5*r6).[31:0], may carry-out
madc.hi.u32    r2,r5,r6,0;    // r2 =(r5*r6).[63:32]+carry-in,
                              // no carry-out
mad.lo.cc.u32   r1,r4,r7,r1;  // r1+=(r4*r7).[31:0], may carry-out
madc.hi.cc.u32  r2,r4,r7,r2;  // r2+=(r4*r7).[63:32]+carry-in,
                              // may carry-out
addc.u32        r3,0,0;       // r3 = carry-in, no carry-out
mad.lo.cc.u32   r2,r5,r7,r2;  // r2+=(r5*r7).[31:0], may carry-out
madc.hi.u32     r3,r5,r7,r3;  // r3+=(r5*r7).[63:32]+carry-in

9.7.3. Floating-Point Instructions

Floating-point instructions operate on .f32 and .f64 register operands and constant immediate values. The floating-point instructions are:

  • testp
  • copysign
  • add
  • sub
  • mul
  • fma
  • mad
  • div
  • abs
  • neg
  • min
  • max
  • rcp
  • sqrt
  • rsqrt
  • sin
  • cos
  • lg2
  • ex2

Instructions that support rounding modifiers are IEEE-754 compliant. Double-precision instructions support subnormal inputs and results. Single-precision instructions support subnormal inputs and results by default for sm_20 and subsequent targets, and flush subnormal inputs and results to sign-preserving zero for sm_1x targets. The optional .ftz modifier on single-precision instructions provides backward compatibility with sm_1x targets by flushing subnormal inputs and results to sign-preserving zero regardless of the target architecture.

Single-precision add, sub, mul, and mad support saturation of results to the range [0.0, 1.0], with NaNs being flushed to positive zero. NaN payloads are supported for double-precision instructions (except for rcp.approx.ftz.f64 and rsqrt.approx.ftz.f64, which maps input NaNs to a canonical NaN). Single-precision instructions return an unspecified NaN. Note that future implementations may support NaN payloads for single-precision instructions, so PTX programs should not rely on the specific single-precision NaNs being generated.

Table 26 summarizes floating-point instructions in PTX.

Table 26. Summary of Floating-Point Instructions
Instruction .rn .rz .rm .rp .ftz .sat Notes
{add,sub,mul}.rnd.f32 x x x x x x If no rounding modifier is specified, default is .rn and instructions may be folded into a multiply-add.
{add,sub,mul}.rnd.f64 x x x x n/a n/a If no rounding modifier is specified, default is .rn and instructions may be folded into a multiply-add.
mad.f32 n/a n/a n/a n/a x x

.target sm_1x

No rounding modifier.
{mad,fma}.rnd.f32 x x x x x x

.target sm_20 or higher

mad.f32 and fma.f32 are the same.

{mad,fma}.rnd.f64 x x x x n/a n/a mad.f64 and fma.f64 are the same.
div.full.f32 n/a n/a n/a n/a x n/a No rounding modifier.
{div,rcp,sqrt}.approx.f32 n/a n/a n/a n/a x n/a n/a
rcp.approx.ftz.f64 n/a n/a n/a n/a x n/a .target sm_20 or higher
{div,rcp,sqrt}.rnd.f32 x x x x x n/a .target sm_20 or higher
{div,rcp,sqrt}.rnd.f64 x x x x n/a n/a .target sm_20 or higher
{abs,neg,min,max}.f32 n/a n/a n/a n/a x n/a  
{abs,neg,min,max}.f64 n/a n/a n/a n/a n/a n/a  
rsqrt.approx.f32 n/a n/a n/a n/a x n/a  
rsqrt.approx.f64 n/a n/a n/a n/a n/a n/a  
rsqrt.approx.ftz.f64 n/a n/a n/a n/a x n/a .target sm_20 or higher
{sin,cos,lg2,ex2}.approx.f32 n/a n/a n/a n/a x n/a  

9.7.3.1. Floating Point Instructions: testp

testp

Test floating-point property.

Syntax
testp.op.type  p, a;  // result is .pred

.op   = { .finite, .infinite,
          .number, .notanumber,
          .normal, .subnormal };
.type = { .f32, .f64 };
Description

testp tests common properties of floating-point numbers and returns a predicate value of 1 if True and 0 if False.

testp.finite
True if the input is not infinite or NaN
testp.infinite
True if the input is positive or negative infinity
testp.number
True if the input is not NaN
testp.notanumber
True if the input is NaN
testp.normal
True if the input is a normal number (not NaN, not infinity)
testp.subnormal
True if the input is a subnormal number (not NaN, not infinity)

As a special case, positive and negative zero are considered normal numbers.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

Requires sm_20 or higher.

Examples
    testp.notanumber.f32  isnan, f0;
    testp.infinite.f64    p, X;

9.7.3.2. Floating Point Instructions: copysign

copysign

Copy sign of one input to another.

Syntax
copysign.type  d, a, b;

.type = { .f32, .f64 };
Description

Copy sign bit of a into value of b, and return the result as d.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

Requires sm_20 or higher.

Examples
    copysign.f32  x, y, z;
    copysign.f64  A, B, C;

9.7.3.3. Floating Point Instructions: add

add

Add two values.

Syntax
add{.rnd}{.ftz}{.sat}.f32  d, a, b;
add{.rnd}.f64              d, a, b;

.rnd = { .rn, .rz, .rm, .rp };
Description

Performs addition and writes the resulting value into a destination register.

Semantics
d = a + b;
Notes
Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

add.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

add.f64 supports subnormal numbers.

add.f32 flushes subnormal inputs and results to sign-preserving zero.

Saturation modifier:

add.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

An add instruction with an explicit rounding modifier treated conservatively by the code optimizer. An add instruction with no rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code optimizer. In particular, mul/add sequences with no rounding modifiers may be optimized to use fused-multiply-add instructions on the target device.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

add.f32 supported on all target architectures.

add.f64 requires sm_13 or higher.

Rounding modifiers have the following target requirements:

.rn, .rz
available for all targets
.rm, .rp

for add.f64, requires sm_13 or higher.

for add.f32, requires sm_20 or higher.

Examples
@p  add.rz.ftz.f32  f1,f2,f3;

9.7.3.4. Floating Point Instructions: sub

sub

Subtract one value from another.

Syntax
sub{.rnd}{.ftz}{.sat}.f32  d, a, b;
sub{.rnd}.f64              d, a, b;

.rnd = { .rn, .rz, .rm, .rp };
Description

Performs subtraction and writes the resulting value into a destination register.

Semantics
d = a - b;
Notes
Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

sub.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

sub.f64 supports subnormal numbers.

sub.f32 flushes subnormal inputs and results to sign-preserving zero.

Saturation modifier:

sub.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

A sub instruction with an explicit rounding modifier treated conservatively by the code optimizer. A sub instruction with no rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code optimizer. In particular, mul/sub sequences with no rounding modifiers may be optimized to use fused-multiply-add instructions on the target device.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

sub.f32 supported on all target architectures.

sub.f64 requires sm_13 or higher.

Rounding modifiers have the following target requirements:
.rn, .rz
available for all targets
.rm, .rp

for sub.f64, requires sm_13 or higher.

for sub.f32, requires sm_20 or higher.

Examples
    sub.f32 c,a,b;
    sub.rn.ftz.f32  f1,f2,f3;

9.7.3.5. Floating Point Instructions: mul

mul

Multiply two values.

Syntax
mul{.rnd}{.ftz}{.sat}.f32  d, a, b;
mul{.rnd}.f64              d, a, b;

.rnd = { .rn, .rz, .rm, .rp };
Description

Compute the product of two values.

Semantics
d = a * b;
Notes

For floating-point multiplication, all operands must be the same size.

Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

mul.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

mul.f64 supports subnormal numbers.

mul.f32 flushes subnormal inputs and results to sign-preserving zero.

Saturation modifier:

mul.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

A mul instruction with an explicit rounding modifier treated conservatively by the code optimizer. A mul instruction with no rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code optimizer. In particular, mul/add and mul/sub sequences with no rounding modifiers may be optimized to use fused-multiply-add instructions on the target device.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

mul.f32 supported on all target architectures.

mul.f64 requires sm_13 or higher.

Rounding modifiers have the following target requirements:
.rn, .rz
available for all targets
.rm, .rp

for mul.f64, requires sm_13 or higher.

for mul.f32, requires sm_20 or higher.

Examples
    mul.ftz.f32 circumf,radius,pi  // a single-precision multiply

9.7.3.6. Floating Point Instructions: fma

fma

Fused multiply-add.

Syntax
fma.rnd{.ftz}{.sat}.f32  d, a, b, c;
fma.rnd.f64              d, a, b, c;

.rnd = { .rn, .rz, .rm, .rp };
Description

Performs a fused multiply-add with no loss of precision in the intermediate product and addition.

Semantics
d = a*b + c;
Notes

fma.f32 computes the product of a and b to infinite precision and then adds c to this product, again in infinite precision. The resulting value is then rounded to single precision using the rounding mode specified by .rnd.

fma.f64 computes the product of a and b to infinite precision and then adds c to this product, again in infinite precision. The resulting value is then rounded to double precision using the rounding mode specified by .rnd.

fma.f64 is the same as mad.f64.

Rounding modifiers (no default):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

fma.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

fma.f64 supports subnormal numbers.

fma.f32 is unimplemented for sm_1x targets.

Saturation:

fma.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

PTX ISA Notes

fma.f64 introduced in PTX ISA version 1.4.

fma.f32 introduced in PTX ISA version 2.0.

Target ISA Notes

fma.f32 requires sm_20 or higher.

fma.f64 requires sm_13 or higher.

Examples
    fma.rn.ftz.f32  w,x,y,z;
@p  fma.rn.f64      d,a,b,c;

9.7.3.7. Floating Point Instructions: mad

mad

Multiply two values and add a third value.

Syntax
mad{.ftz}{.sat}.f32      d, a, b, c;    // .target sm_1x
mad.rnd{.ftz}{.sat}.f32  d, a, b, c;    // .target sm_20
mad.rnd.f64              d, a, b, c;    // .target sm_13 and higher

.rnd = { .rn, .rz, .rm, .rp };
Description

Multiplies two values and adds a third, and then writes the resulting value into a destination register.

Semantics
d = a*b + c;
Notes
For .targetsm_20 and higher:
  • mad.f32 computes the product of a and b to infinite precision and then adds c to this product, again in infinite precision. The resulting value is then rounded to single precision using the rounding mode specified by .rnd.
  • mad.f64 computes the product of a and b to infinite precision and then adds c to this product, again in infinite precision. The resulting value is then rounded to double precision using the rounding mode specified by .rnd.
  • mad.{f32,f64} is the same as fma.{f32,f64}.
For .targetsm_1x:
  • mad.f32 computes the product of a and b at double precision, and then the mantissa is truncated to 23 bits, but the exponent is preserved. Note that this is different from computing the product with mul, where the mantissa can be rounded and the exponent will be clamped. The exception for mad.f32 is when c = +/-0.0, mad.f32 is identical to the result computed using separate mul and add instructions. When JIT-compiled for SM 2.0 devices, mad.f32 is implemented as a fused multiply-add (i.e., fma.rn.ftz.f32). In this case, mad.f32 can produce slightly different numeric results and backward compatibility is not guaranteed in this case.
  • mad.f64 computes the product of a and b to infinite precision and then adds c to this product, again in infinite precision. The resulting value is then rounded to double precision using the rounding mode specified by .rnd. Unlike mad.f32, the treatment of subnormal inputs and output follows IEEE 754 standard.
  • mad.f64 is the same as fma.f64.
Rounding modifiers (no default):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

mad.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

mad.f64 supports subnormal numbers.

mad.f32 flushes subnormal inputs and results to sign-preserving zero.

Saturation modifier:

mad.sat.f32 clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

In PTX ISA versions 1.4 and later, a rounding modifier is required for mad.f64.

Legacy mad.f64 instructions having no rounding modifier will map to mad.rn.f64.

In PTX ISA versions 2.0 and later, a rounding modifier is required for mad.f32 for sm_20 and higher targets.

Errata

mad.f32 requires a rounding modifier for sm_20 and higher targets. However for PTX ISA version 3.0 and earlier, ptxas does not enforce this requirement and mad.f32 silently defaults to mad.rn.f32. For PTX ISA version 3.1, ptxas generates a warning and defaults to mad.rn.f32, and in subsequent releases ptxas will enforce the requirement for PTX ISA version 3.2 and later.

Target ISA Notes

mad.f32 supported on all target architectures.

mad.f64 requires sm_13 or higher.

Rounding modifiers have the following target requirements:
  • .rn,.rz,.rm,.rp for mad.f64, requires sm_13 or higher.
  • .rn,.rz,.rm,.rp for mad.f32, requires sm_20 or higher.
Examples
@p  mad.f32  d,a,b,c;

9.7.3.8. Floating Point Instructions: div

div

Divide one value by another.

Syntax
div.approx{.ftz}.f32  d, a, b;  // fast, approximate divide
div.full{.ftz}.f32    d, a, b;  // full-range approximate divide
div.rnd{.ftz}.f32     d, a, b;  // IEEE 754 compliant rounding
div.rnd.f64           d, a, b;  // IEEE 754 compliant rounding

.rnd = { .rn, .rz, .rm, .rp };
Description

Divides a by b, stores result in d.

Semantics
d = a / b;
Notes

Fast, approximate single-precision divides:

  • div.approx.f32 implements a fast approximation to divide, computed as d = a * (1/b). For b in [2-126, 2126], the maximum ulp error is 2.
  • div.full.f32 implements a relatively fast, full-range approximation that scales operands to achieve better accuracy, but is not fully IEEE 754 compliant and does not support rounding modifiers. The maximum ulp error is 2 across the full range of inputs.
  • Subnormal inputs and results are flushed to sign-preserving zero. Fast, approximate division by zero creates a value of infinity (with same sign as a).

Divide with IEEE 754 compliant rounding:

Rounding modifiers (no default):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+
By default, subnormal numbers are supported.

div.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x
div.f64 supports subnormal numbers.

div.f32 flushes subnormal inputs and results to sign-preserving zero.

PTX ISA Notes

div.f32 and div.f64 introduced in PTX ISA version 1.0.

Explicit modifiers .approx, .full, .ftz, and rounding introduced in PTX ISA version 1.4.

For PTX ISA version 1.4 and later, one of .approx, .full, or .rnd is required.

For PTX ISA versions 1.0 through 1.3, div.f32 defaults to div.approx.ftz.f32, and div.f64 defaults to div.rn.f64.

Target ISA Notes

div.approx.f32 and div.full.f32 supported on all target architectures.

div.rnd.f32 requires sm_20 or higher.

div.rn.f64 requires sm_13 or higher, or .target map_f64_to_f32.

div.{rz,rm,rp}.f64 requires sm_20 or higher.

Examples
    div.approx.ftz.f32  diam,circum,3.14159;
    div.full.ftz.f32    x, y, z;
    div.rn.f64          xd, yd, zd;

9.7.3.9. Floating Point Instructions: abs

abs

Absolute value.

Syntax
abs{.ftz}.f32  d, a;
abs.f64        d, a;
Description

Take the absolute value of a and store the result in d.

Semantics
d = |a|;
Notes
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

abs.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

abs.f64 supports subnormal numbers.

abs.f32 flushes subnormal inputs and results to sign-preserving zero.

NaN inputs yield an unspecified NaN. Future implementations may comply with the IEEE 754 standard by preserving payload and modifying only the sign bit.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

abs.f32 supported on all target architectures.

abs.f64 requires sm_13 or higher.

Examples
    abs.ftz.f32  x,f0;

9.7.3.10. Floating Point Instructions: neg

neg

Arithmetic negate.

Syntax
neg{.ftz}.f32  d, a;
neg.f64        d, a;
Description

Negate the sign of a and store the result in d.

Semantics
d = -a;
Notes
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

neg.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

neg.f64 supports subnormal numbers.

neg.f32 flushes subnormal inputs and results to sign-preserving zero.

NaN inputs yield an unspecified NaN. Future implementations may comply with the IEEE 754 standard by preserving payload and modifying only the sign bit.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

neg.f32 supported on all target architectures.

neg.f64 requires sm_13 or higher.

Examples
    neg.ftz.f32  x,f0;

9.7.3.11. Floating Point Instructions: min

min

Find the minimum of two values.

Syntax
min{.ftz}.f32  d, a, b;
min.f64        d, a, b;
Description

Store the minimum of a and b in d.

Semantics
if (isNaN(a) && isNaN(b))    d = NaN;
else if (isNaN(a))           d = b;
else if (isNaN(b))           d = a;
else                         d = (a < b) ? a : b;
Notes
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

min.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

min.f64 supports subnormal numbers.

min.f32 flushes subnormal inputs and results to sign-preserving zero.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

min.f32 supported on all target architectures.

min.f64 requires sm_13 or higher.

Examples
@p  min.ftz.f32  z,z,x;
    min.f64      a,b,c;

9.7.3.12. Floating Point Instructions: max

max

Find the maximum of two values.

Syntax
max{.ftz}.f32  d, a, b;
max.f64        d, a, b;
Description

Store the maximum of a and b in d.

Semantics
if (isNaN(a) && isNaN(b))    d = NaN;
else if (isNaN(a))          d = b;
else if (isNaN(b))          d = a;
else                        d = (a > b) ? a : b;
Notes
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

max.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

max.f64 supports subnormal numbers.

max.f32 flushes subnormal inputs and results to sign-preserving zero.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

max.f32 supported on all target architectures.

max.f64 requires sm_13 or higher.

Examples
    max.ftz.f32  f0,f1,f2;
    max.f64      a,b,c;

9.7.3.13. Floating Point Instructions: rcp

rcp

Take the reciprocal of a value.

Syntax
rcp.approx{.ftz}.f32  d, a;  // fast, approximate reciprocal
rcp.rnd{.ftz}.f32     d, a;  // IEEE 754 compliant rounding
rcp.rnd.f64           d, a;  // IEEE 754 compliant rounding

.rnd = { .rn, .rz, .rm, .rp };
Description

Compute 1/a, store result in d.

Semantics
d = 1 / a;
Notes

Fast, approximate single-precision reciprocal:

rcp.approx.f32 implements a fast approximation to reciprocal. The maximum absolute error is 2-23.0 over the range 1.0-2.0.

Input Result
-Inf -0.0
-subnormal -Inf
-0.0 -Inf
+0.0 +Inf
+subnormal +Inf
+Inf +0.0
NaN NaN

Reciprocal with IEEE 754 compliant rounding:

Rounding modifiers (no default):

.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity

Subnormal numbers:

sm_20+

By default, subnormal numbers are supported.

rcp.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

rcp.f64 supports subnormal numbers.

rcp.f32 flushes subnormal inputs and results to sign-preserving zero.

PTX ISA Notes

rcp.f32 and rcp.f64 introduced in PTX ISA version 1.0. rcp.rn.f64 and explicit modifiers .approx and .ftz were introduced in PTX ISA version 1.4. General rounding modifiers were added in PTX ISA version 2.0.

For PTX ISA version 1.4 and later, one of .approx or .rnd is required.

For PTX ISA versions 1.0 through 1.3, rcp.f32 defaults to rcp.approx.ftz.f32, and rcp.f64 defaults to rcp.rn.f64.

Target ISA Notes

rcp.approx.f32 supported on all target architectures.

rcp.rnd.f32 requires sm_20 or higher.

rcp.rn.f64 requires sm_13 or higher, or .target map_f64_to_f32.

rcp.{rz,rm,rp}.f64 requires sm_20 or higher.

Examples
    rcp.approx.ftz.f32  ri,r;
    rcp.rn.ftz.f32      xi,x;
    rcp.rn.f64          xi,x;

9.7.3.14. Floating Point Instructions: rcp.approx.ftz.f64

rcp.approx.ftz.f64

Compute a fast, gross approximation to the reciprocal of a value.

Syntax
rcp.approx.ftz.f64  d, a;
Description
Compute a fast, gross approximation to the reciprocal as follows:
  1. extract the most-significant 32 bits of .f64 operand a in 1.11.20 IEEE floating-point format (i.e., ignore the least-significant 32 bits of a),
  2. compute an approximate .f64 reciprocal of this value using the most-significant 20 bits of the mantissa of operand a,
  3. place the resulting 32-bits in 1.11.20 IEEE floating-point format in the most-significant 32-bits of destination d,and
  4. zero the least significant 32 mantissa bits of .f64 destination d.
Semantics
tmp = a[63:32]; // upper word of a, 1.11.20 format
d[63:32] = 1.0 / tmp;
d[31:0] = 0x00000000;
Notes

rcp.approx.ftz.f64 implements a fast, gross approximation to reciprocal.

Input a[63:32] Result d[63:32]
-Inf -0.0
-subnormal -Inf
-0.0 -Inf
+0.0 +Inf
+subnormal +Inf
+Inf +0.0
NaN NaN

Input NaNs map to a canonical NaN with encoding 0x7fffffff00000000.

Subnormal inputs and results are flushed to sign-preserving zero.

PTX ISA Notes

rcp.approx.ftz.f64 introduced in PTX ISA version 2.1.

Target ISA Notes

rcp.approx.ftz.f64 requires sm_20 or higher.

Examples
    rcp.ftz.f64  xi,x;

9.7.3.15. Floating Point Instructions: sqrt

sqrt

Take the square root of a value.

Syntax
sqrt.approx{.ftz}.f32  d, a; // fast, approximate square root
sqrt.rnd{.ftz}.f32     d, a; // IEEE 754 compliant rounding
sqrt.rnd.f64           d, a; // IEEE 754 compliant rounding

.rnd = { .rn, .rz, .rm, .rp };
Description

Compute sqrt(a) and store the result in d.

Semantics
d = sqrt(a);
Notes

sqrt.approx.f32 implements a fast approximation to square root. The maximum absolute error for sqrt.approx.f32 is TBD.

Input Result
-Inf NaN
-normal NaN
-subnormal -0.0
-0.0 -0.0
+0.0 +0.0
+subnormal +0.0
+Inf +Inf
NaN NaN

Square root with IEEE 754 compliant rounding:

Rounding modifiers (no default):
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

sqrt.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

sqrt.f64 supports subnormal numbers.

sqrt.f32 flushes subnormal inputs and results to sign-preserving zero.

PTX ISA Notes

sqrt.f32 and sqrt.f64 introduced in PTX ISA version 1.0. sqrt.rn.f64 and explicit modifiers .approx and .ftz were introduced in PTX ISA version 1.4. General rounding modifiers were added in PTX ISA version 2.0.

For PTX ISA version 1.4 and later, one of .approx or .rnd is required.

For PTX ISA versions 1.0 through 1.3, sqrt.f32 defaults to sqrt.approx.ftz.f32, and sqrt.f64 defaults to sqrt.rn.f64.

Target ISA Notes

sqrt.approx.f32 supported on all target architectures.

sqrt.rnd.f32 requires sm_20 or higher.

sqrt.rn.f64 requires sm_13 or higher, or .target map_f64_to_f32.

sqrt.{rz,rm,rp}.f64 requires sm_20 or higher.

Examples
    sqrt.approx.ftz.f32  r,x;
    sqrt.rn.ftz.f32      r,x;
    sqrt.rn.f64          r,x;

9.7.3.16. Floating Point Instructions: rsqrt

rsqrt

Take the reciprocal of the square root of a value.

Syntax
rsqrt.approx{.ftz}.f32  d, a;
rsqrt.approx.f64        d, a;
Description

Compute 1/sqrt(a) and store the result in d.

Semantics
d = 1/sqrt(a);
Notes

rsqrt.approx implements an approximation to the reciprocal square root.

Input Result
-Inf NaN
-normal NaN
-subnormal -Inf
-0.0 -Inf
+0.0 +Inf
+subnormal +Inf
+Inf +0.0
NaN NaN

The maximum absolute error for rsqrt.f32 is 2-22.4 over the range 1.0-4.0.

The maximum absolute error for rsqrt.f64 is TBD.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

rsqrt.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x

rsqrt.f64 supports subnormal numbers.

rsqrt.f32 flushes subnormal inputs and results to sign-preserving zero.

Note that rsqrt.approx.f64 is emulated in software and are relatively slow.

PTX ISA Notes

rsqrt.f32 and rsqrt.f64 were introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz were introduced in PTX ISA version 1.4.

For PTX ISA version 1.4 and later, the .approx modifier is required.

For PTX ISA versions 1.0 through 1.3, rsqrt.f32 defaults to rsqrt.approx.ftz.f32, and rsqrt.f64 defaults to rsqrt.approx.f64.

Target ISA Notes

rsqrt.f32 supported on all target architectures.

rsqrt.f64 requires sm_13 or higher.

Examples
    rsqrt.approx.ftz.f32  isr, x;
    rsqrt.approx.f64      ISR, X;

9.7.3.17. Floating Point Instructions: rsqrt.approx.ftz.f64

rsqrt.approx.ftz.f64

Compute an approximation of the square root reciprocal of a value.

Syntax
rsqrt.approx.ftz.f64 d, a;
Description

Compute a double-precision (.f64) approximation of the square root reciprocal of a value. The least significant 32 bits of the double-precision (.f64) destination d are all zeros.

Semantics
tmp = a[63:32]; // upper word of a, 1.11.20 format
d[63:32] = 1.0 / sqrt(tmp);
d[31:0] = 0x00000000;
Notes

rsqrt.approx.ftz.f64 implements a fast approximation of the square root reciprocal of a value.

Input Result
-Inf NaN
-subnormal -Inf
-0.0 -Inf
+0.0 +Inf
+subnormal +Inf
+Inf +0.0
NaN NaN

Input NaNs map to a canonical NaN with encoding 0x7fffffff00000000.

Subnormal inputs and results are flushed to sign-preserving zero.

PTX ISA Notes

rsqrt.approx.ftz.f64 introduced in PTX ISA version 4.0.

Target ISA Notes

rsqrt.approx.ftz.f64 requires sm_20 or higher.

Examples
    rsqrt.approx.ftz.f64 xi,x;

9.7.3.18. Floating Point Instructions: sin

sin

Find the sine of a value.

Syntax
sin.approx{.ftz}.f32  d, a;
Description

Find the sine of the angle a (in radians).

Semantics
d = sin(a);
Notes

sin.approx.f32 implements a fast approximation to sine.

Input Result
-Inf NaN
-subnormal -0.0
-0.0 -0.0
+0.0 +0.0
+subnormal +0.0
+Inf NaN
NaN NaN

The maximum absolute error is 2-20.9 in quadrant 00.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

sin.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x
Subnormal inputs and results to sign-preserving zero.
PTX ISA Notes

sin.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz introduced in PTX ISA version 1.4.

For PTX ISA version 1.4 and later, the .approx modifier is required.

For PTX ISA versions 1.0 through 1.3, sin.f32 defaults to sin.approx.ftz.f32.

Target ISA Notes

Supported on all target architectures.

Examples
    sin.approx.ftz.f32  sa, a;

9.7.3.19. Floating Point Instructions: cos

cos

Find the cosine of a value.

Syntax
cos.approx{.ftz}.f32  d, a;
Description

Find the cosine of the angle a (in radians).

Semantics
d = cos(a);
Notes

cos.approx.f32 implements a fast approximation to cosine.

Input Result
-Inf NaN
-subnormal +1.0
-0.0 +1.0
+0.0 +1.0
+subnormal +1.0
+Inf NaN
NaN NaN

The maximum absolute error is 2-20.9 in quadrant 00.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

cos.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x
Subnormal inputs and results to sign-preserving zero.
PTX ISA Notes

cos.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz introduced in PTX ISA version 1.4.

For PTX ISA version 1.4 and later, the .approx modifier is required.

For PTX ISA versions 1.0 through 1.3, cos.f32 defaults to cos.approx.ftz.f32.

Target ISA Notes

Supported on all target architectures.

Examples
    cos.approx.ftz.f32  ca, a;

9.7.3.20. Floating Point Instructions: lg2

lg2

Find the base-2 logarithm of a value.

Syntax
lg2.approx{.ftz}.f32  d, a;
Description

Determine the log2 of a.

Semantics
d = log(a) / log(2);
Notes

lg2.approx.f32 implements a fast approximation to log2(a).

Input Result
-Inf NaN
-subnormal -Inf
-0.0 -Inf
+0.0 -Inf
+subnormal -Inf
+Inf +Inf
NaN NaN

The maximum absolute error is 2-22.6 for mantissa.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

lg2.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x
Subnormal inputs and results to sign-preserving zero.
PTX ISA Notes

lg2.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz introduced in PTX ISA version 1.4.

For PTX ISA version 1.4 and later, the .approx modifier is required.

For PTX ISA versions 1.0 through 1.3, lg2.f32 defaults to lg2.approx.ftz.f32.

Target ISA Notes

Supported on all target architectures.

Examples
    lg2.approx.ftz.f32  la, a;

9.7.3.21. Floating Point Instructions: ex2

ex2

Find the base-2 exponential of a value.

Syntax
ex2.approx{.ftz}.f32  d, a;
Description

Raise 2 to the power a.

Semantics
d = 2 ^ a;
Notes

ex2.approx.f32 implements a fast approximation to 2a.

Input Result
-Inf +0.0
-subnormal +1.0
-0.0 +1.0
+0.0 +1.0
+subnormal +1.0
+Inf +Inf
NaN NaN

The maximum absolute error is 2-22.5 for fraction in the primary range.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

ex2.ftz.f32 flushes subnormal inputs and results to sign-preserving zero.

sm_1x
Subnormal inputs and results to sign-preserving zero.
PTX ISA Notes

ex2.f32 introduced in PTX ISA version 1.0. Explicit modifiers .approx and .ftz introduced in PTX ISA version 1.4.

For PTX ISA version 1.4 and later, the .approx modifier is required.

For PTX ISA versions 1.0 through 1.3, ex2.f32 defaults to ex2.approx.ftz.f32.

Target ISA Notes

Supported on all target architectures.

Examples
    ex2.approx.ftz.f32  xa, a;

9.7.4. Half Precision Floating-Point Instructions

Half precision floating-point instructions operate on .f16 and .f16x2 register operands. The half precision floating-point instructions are:

  • add
  • sub
  • mul
  • fma
  • neg

Half-precision add, sub, mul, and fma support saturation of results to the range [0.0, 1.0], with NaNs being flushed to positive zero. Half-precision instructions return an unspecified NaN.

9.7.4.1. Half Precision Floating Point Instructions: add

add

Add two values.

Syntax
add{.rnd}{.ftz}{.sat}.f16   d, a, b;
add{.rnd}{.ftz}{.sat}.f16x2 d, a, b;

.rnd = { .rn };
Description

Performs addition and writes the resulting value into a destination register.

For .f16x2 instruction type, forms input vectors by half word values from source operands. Half-word operands are then added in parallel to produce .f16x2 result in destination.

For .f16 instruction type, operands d, a and b have .f16 or .b16 type. For .f16x2 instruction type, operands d, a and b have .b32 type.

Semantics
if (type == f16) { 
    d = a + b;
} else if (type == f16x2) {
    fA[0] = a[0:15];
    fA[1] = a[16:31];
    fB[0] = b[0:15];
    fB[1] = b[16:31];
    for (i = 0; i < 2; i++) {
         d[i] = fA[i] + fB[i];
    }
}
Notes
Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
Subnormal numbers:
By default, subnormal numbers are supported.
add.ftz.{f16, f16x2} flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
add.sat.{f16, f16x2} clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

An add instruction with an explicit rounding modifier treated conservatively by the code optimizer. An add instruction with no rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code optimizer. In particular, mul/add sequences with no rounding modifiers may be optimized to use fused-multiply-add instructions on the target device.

PTX ISA Notes

Introduced in PTX ISA version 4.2.

Target ISA Notes

Requires sm_53 or higher.

Examples
     // scalar f16 additions
     add.f16        d0, a0, b0;
     add.rn.f16     d1, a1, b1;
     
     // SIMD f16 addition
     cvt.rn.f16.f32 h0, f0;
     cvt.rn.f16.f32 h1, f1;
     cvt.rn.f16.f32 h2, f2;
     cvt.rn.f16.f32 h3, f3;
     mov.b32  p1, {h0, h1};   // pack two f16 to 32bit f16x2
     mov.b32  p2, {h2, h3};   // pack two f16 to 32bit f16x2
     add.f16x2  p3, p1, p2;   // SIMD f16x2 addition
     // SIMD fp16 addition
     ld.global.b32   f0, [addr];     // load 32 bit which hold packed f16x2
     ld.global.b32   f1, [addr + 4]; // load 32 bit which hold packed f16x2
     add.f16x2       f2, f0, f1;     // SIMD f16x2 addition

9.7.4.2. Half Precision Floating Point Instructions: sub

sub

Subtract two values.

Syntax
sub{.rnd}{.ftz}{.sat}.f16   d, a, b;
sub{.rnd}{.ftz}{.sat}.f16x2 d, a, b;

.rnd = { .rn };
Description

Performs subtraction and writes the resulting value into a destination register.

For .f16x2 instruction type, forms input vectors by half word values from source operands. Half-word operands are then subtracted in parallel to produce .f16x2 result in destination.

For .f16 instruction type, operands d, a and b have .f16 or .b16 type. For .f16x2 instruction type, operands d, a and b have .b32 type.

Semantics
if (type == f16) { 
    d = a - b;
} else if (type == f16x2) {
    fA[0] = a[0:15];
    fA[1] = a[16:31];
    fB[0] = b[0:15];
    fB[1] = b[16:31];
    for (i = 0; i < 2; i++) {
         d[i] = fA[i] - fB[i];
    }
}
Notes
Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
Subnormal numbers:
By default, subnormal numbers are supported.
sub.ftz.{f16, f16x2} flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
sub.sat.{f16, f16x2} clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

A sub instruction with an explicit rounding modifier treated conservatively by the code optimizer. A sub instruction with no rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code optimizer. In particular, mul/sub sequences with no rounding modifiers may be optimized to use fused-multiply-add instructions on the target device.

PTX ISA Notes

Introduced in PTX ISA version 4.2.

Target ISA Notes

Requires sm_53 or higher.

Examples
     // scalar f16 subtractions
     sub.f16        d0, a0, b0;
     sub.rn.f16     d1, a1, b1;
     
     // SIMD f16 subtraction
     cvt.rn.f16.f32 h0, f0;
     cvt.rn.f16.f32 h1, f1;
     cvt.rn.f16.f32 h2, f2;
     cvt.rn.f16.f32 h3, f3;
     mov.b32  p1, {h0, h1};   // pack two f16 to 32bit f16x2
     mov.b32  p2, {h2, h3};   // pack two f16 to 32bit f16x2
     sub.f16x2  p3, p1, p2;   // SIMD f16x2 subtraction
     // SIMD fp16 subtraction
     ld.global.b32   f0, [addr];     // load 32 bit which hold packed f16x2
     ld.global.b32   f1, [addr + 4]; // load 32 bit which hold packed f16x2
     sub.f16x2       f2, f0, f1;     // SIMD f16x2 subtraction

9.7.4.3. Half Precision Floating Point Instructions: mul

mul

Multiply two values.

Syntax
mul{.rnd}{.ftz}{.sat}.f16   d, a, b;
mul{.rnd}{.ftz}{.sat}.f16x2 d, a, b;

.rnd = { .rn };
Description

Performs multiplication and writes the resulting value into a destination register.

For .f16x2 instruction type, forms input vectors by half word values from source operands. Half-word operands are then multiplied in parallel to produce .f16x2 result in destination.

For .f16 instruction type, operands d, a and b have .f16 or .b16 type. For .f16x2 instruction type, operands d, a and b have .b32 type.

Semantics
if (type == f16) { 
    d = a * b;
} else if (type == f16x2) {
    fA[0] = a[0:15];
    fA[1] = a[16:31];
    fB[0] = b[0:15];
    fB[1] = b[16:31];
    for (i = 0; i < 2; i++) {
         d[i] = fA[i] * fB[i];
    }
}
Notes
Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
Subnormal numbers:
By default, subnormal numbers are supported.
mul.ftz.{f16, f16x2} flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
mul.sat.{f16, f16x2} clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.

A mul instruction with an explicit rounding modifier treated conservatively by the code optimizer. A mul instruction with no rounding modifier defaults to round-to-nearest-even and may be optimized aggressively by the code optimizer. In particular, mul/add sequences with no rounding modifiers may be optimized to use fused-multiply-add instructions on the target device.

PTX ISA Notes

Introduced in PTX ISA version 4.2.

Target ISA Notes

Requires sm_53 or higher.

Examples
     // scalar f16 multiplications
     mul.f16        d0, a0, b0;
     mul.rn.f16     d1, a1, b1;
     
     // SIMD f16 multiplication
     cvt.rn.f16.f32 h0, f0;
     cvt.rn.f16.f32 h1, f1;
     cvt.rn.f16.f32 h2, f2;
     cvt.rn.f16.f32 h3, f3;
     mov.b32  p1, {h0, h1};   // pack two f16 to 32bit f16x2
     mov.b32  p2, {h2, h3};   // pack two f16 to 32bit f16x2
     mul.f16x2  p3, p1, p2;   // SIMD f16x2 multiplication
     // SIMD fp16 multiplication
     ld.global.b32   f0, [addr];     // load 32 bit which hold packed f16x2
     ld.global.b32   f1, [addr + 4]; // load 32 bit which hold packed f16x2
     mul.f16x2       f2, f0, f1;     // SIMD f16x2 multiplication

9.7.4.4. Half Precision Floating Point Instructions: fma

fma

Fused multiply-add

Syntax
fma.rnd{.ftz}{.sat}.f16   d, a, b, c;
fma.rnd{.ftz}{.sat}.f16x2 d, a, b;

.rnd = { .rn };
Description

Performs a fused multiply-add with no loss of precision in the intermediate product and addition.

For .f16x2 instruction type, forms input vectors by half word values from source operands. Half-word operands are then operated in parallel to produce .f16x2 result in destination.

For .f16 instruction type, operands d, a, b and c have .f16 or .b16 type. For .f16x2 instruction type, operands d, a, b and c have .b32 type.

Semantics
if (type == f16) { 
    d = a * b + c;
} else if (type == f16x2) {
    fA[0] = a[0:15];
    fA[1] = a[16:31];
    fB[0] = b[0:15];
    fB[1] = b[16:31];
    fC[0] = c[0:15];
    fC[1] = c[16:31];
    for (i = 0; i < 2; i++) {
         d[i] = fA[i] * fB[i] + fC[i];
    }
}
Notes
Rounding modifiers (default is .rn):
.rn
mantissa LSB rounds to nearest even
Subnormal numbers:
By default, subnormal numbers are supported.
fma.ftz.{f16, f16x2} flushes subnormal inputs and results to sign-preserving zero.
Saturation modifier:
fma.sat.{f16, f16x2} clamps the result to [0.0, 1.0]. NaN results are flushed to +0.0f.
PTX ISA Notes

Introduced in PTX ISA version 4.2.

Target ISA Notes

Requires sm_53 or higher.

Examples
     // scalar f16 fused multiply-add
     fma.f16        d0, a0, b0, c0;
     fma.rn.f16     d1, a1, b1, c1;
     
     // SIMD f16 fused multiply-add
     cvt.rn.f16.f32 h0, f0;
     cvt.rn.f16.f32 h1, f1;
     cvt.rn.f16.f32 h2, f2;
     cvt.rn.f16.f32 h3, f3;
     mov.b32  p1, {h0, h1}; // pack two f16 to 32bit f16x2
     mov.b32  p2, {h2, h3}; // pack two f16 to 32bit f16x2
     fma.f16x2  p3, p1, p2, p2;   // SIMD f16x2 fused multiply-add
     // SIMD fp16 fused multiply-add
     ld.global.b32   f0, [addr];     // load 32 bit which hold packed f16x2
     ld.global.b32   f1, [addr + 4]; // load 32 bit which hold packed f16x2
     fma.f16x2       f2, f0, f1, f1; // SIMD f16x2 fused multiply-add

9.7.5. Comparison and Selection Instructions

The comparison select instructions are:
  • set
  • setp
  • selp
  • slct

As with single-precision floating-point instructions, the set, setp, and slct instructions support subnormal numbers for sm_20 and higher targets and flush single-precision subnormal inputs to sign-preserving zero for sm_1x targets. The optional .ftz modifier provides backward compatibility with sm_1x targets by flushing subnormal inputs and results to sign-preserving zero regardless of the target architecture.

9.7.5.1. Comparison and Selection Instructions: set

set

Compare two numeric values with a relational operator, and optionally combine this result with a predicate value by applying a Boolean operator.

Syntax
set.CmpOp{.ftz}.dtype.stype         d, a, b;
set.CmpOp.BoolOp{.ftz}.dtype.stype  d, a, b, {!}c;

.CmpOp  = { eq, ne, lt, gt, ge, lo, ls, hi, hs,
            equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.dtype  = { .u32, .s32, .f32 };
.stype  = { .b16, .b32, .b64,
            .u16, .u32, .u64,
            .s16, .s32, .s64,
                  .f32, .f64 };
Description

Compares two numeric values and optionally combines the result with another predicate value by applying a Boolean operator. If this result is True, 1.0f is written for floating-point destination types, and 0xffffffff is written for integer destination types. Otherwise, 0x00000000 is written.

Operand d has type .dtype; operands a and b have type .stype; operand c has type .pred.

Semantics
t = (a CmpOp b) ? 1 : 0;
if (isFloat(dtype))
    d = BoolOp(t, c) ? 1.0f : 0x00000000;
else
    d = BoolOp(t, c) ? 0xffffffff : 0x00000000;
Integer Notes

The signed and unsigned comparison operators are eq, ne, lt, le, gt, ge.

For unsigned values, the comparison operators lo, ls, hi, and hs for lower, lower-or-same, higher, and higher-or-same may be used instead of lt, le, gt, ge, respectively.

The untyped, bit-size comparisons are eq and ne.

Floating Point Notes

The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is NaN, the result is False.

To aid comparison operations in the presence of NaN values, unordered versions are included: equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not NaN), then these comparisons have the same result as their ordered counterparts. If either operand is NaN, then the result of these comparisons is True.

num returns True if both operands are numeric values (not NaN), and nan returns True if either operand is NaN.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

set.ftz.dtype.f32 flushes subnormal inputs to sign-preserving zero.

sm_1x

set.dtype.f64 supports subnormal numbers.

set.dtype.f32 flushes subnormal inputs to sign-preserving zero.

Modifier .ftz applies only to .f32 comparisons.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

set with .f64 source type requires sm_13 or higher.

Examples
@p  set.lt.and.f32.s32  d,a,b,r;
    set.eq.u32.u32      d,i,n;

9.7.5.2. Comparison and Selection Instructions: setp

setp

Compare two numeric values with a relational operator, and (optionally) combine this result with a predicate value by applying a Boolean operator.

Syntax
setp.CmpOp{.ftz}.type         p[|q], a, b;
setp.CmpOp.BoolOp{.ftz}.type  p[|q], a, b, {!}c;

.CmpOp  = { eq, ne, lt, gt, ge, lo, ls, hi, hs,
            equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.type   = { .b16, .b32, .b64,
            .u16, .u32, .u64,
            .s16, .s32, .s64,
                  .f32, .f64 };
Description

Compares two values and combines the result with another predicate value by applying a Boolean operator. This result is written to the first destination operand. A related value computed using the complement of the compare result is written to the second destination operand.

Applies to all numeric types. Operands a and b have type .type; operands p, q, and c have type .pred.

Semantics
t = (a CmpOp b) ? 1 : 0;
p = BoolOp(t, c);
q = BoolOp(!t, c);
Integer Notes

The signed and unsigned comparison operators are eq, ne, lt, le, gt, ge.

For unsigned values, the comparison operators lo, ls, hi, and hs for lower, lower-or-same, higher, and higher-or-same may be used instead of lt, le, gt, ge, respectively.

The untyped, bit-size comparisons are eq and ne.

Floating Point Notes

The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is NaN, the result is False.

To aid comparison operations in the presence of NaN values, unordered versions are included: equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not NaN), then these comparisons have the same result as their ordered counterparts. If either operand is NaN, then the result of these comparisons is True.

num returns True if both operands are numeric values (not NaN), and nan returns True if either operand is NaN.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

setp.ftz.dtype.f32 flushes subnormal inputs to sign-preserving zero.

sm_1x

setp.dtype.f64 supports subnormal numbers.

setp.dtype.f32 flushes subnormal inputs to sign-preserving zero.

Modifier .ftz applies only to .f32 comparisons.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

setp with .f64 source type requires sm_13 or higher.

Examples
    setp.lt.and.s32  p|q,a,b,r;
@q  setp.eq.u32      p,i,n;

9.7.5.3. Comparison and Selection Instructions: selp

selp

Select between source operands, based on the value of the predicate source operand.

Syntax
selp.type d, a, b, c;

.type = { .b16, .b32, .b64,
          .u16, .u32, .u64,
          .s16, .s32, .s64,
                .f32, .f64 };
Description

Conditional selection. If c is True, a is stored in d, b otherwise. Operands d, a, and b must be of the same type. Operand c is a predicate.

Semantics
d = (c == 1) ? a : b;
PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

selp.f64 requires sm_13 or higher.

Examples
    selp.s32  r0,r,g,p;
@q  selp.f32  f0,t,x,xp;

9.7.5.4. Comparison and Selection Instructions: slct

slct

Select one source operand, based on the sign of the third operand.

Syntax
slct.dtype.s32        d, a, b, c;
slct{.ftz}.dtype.f32  d, a, b, c;

.dtype = { .b16, .b32, .b64,
           .u16, .u32, .u64,
           .s16, .s32, .s64,
                 .f32, .f64 };
Description

Conditional selection. If c ≥ 0, a is stored in d, otherwise b is stored in d. Operands d, a, and b are treated as a bitsize type of the same width as the first instruction type; operand c must match the second instruction type (.s32 or .f32). The selected input is copied to the output without modification.

Semantics
d = (c >= 0) ? a : b;
Floating Point Notes

For .f32 comparisons, negative zero equals zero.

Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

slct.ftz.dtype.f32 flushes subnormal values of operand c to sign-preserving zero, and operand a is selected.

sm_1x
slct.dtype.f32 flushes subnormal values of operand c to sign-preserving zero, and operand a is selected.

Modifier .ftz applies only to .f32 comparisons.

If operand c is NaN, the comparison is unordered and operand b is selected.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

slct.f64 requires sm_13 or higher.

Examples
    slct.u32.s32  x, y, z, val;
    slct.ftz.u64.f32  A, B, C, fval;

Half Precision Comparison Instructions

The comparison instructions are:
  • set
  • setp

9.7.6.1. Half Precision Comparison Instructions: set

set

Compare two numeric values with a relational operator, and optionally combine this result with a predicate value by applying a Boolean operator.

Syntax
set.CmpOp{.ftz}.f16.stype            d, a, b;
set.CmpOp.BoolOp{.ftz}.f16.stype     d, a, b, {!}c;

set.CmpOp{.ftz}.f16x2.f16x2         d, a, b;
set.CmpOp.BoolOp{.ftz}.f16x2.f16x2  d, a, b, {!}c;

.CmpOp  = { eq, ne, lt, le, gt, ge,
            equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.stype  = { .b16, .b32, .b64,
            .u16, .u32, .u64,
            .s16, .s32, .s64,
                  .f32, .f64 };
Description

Compares two numeric values and optionally combines the result with another predicate value by applying a Boolean operator. If this result is True, 1.0 is written destination types. Otherwise, 0.0 is written.

Operand c has type .pred.

For instruction type .f16, operands a and b have type .stype and operand d has type .b16 or .f16

For instruction type .f16x2, operands a and b have type .stype and operand d has type .b32

Semantics
if (type == .f16) {
     t = (a CmpOp b) ? 1 : 0;
     d = BoolOp(t, c) ? 1.0 : 0.0;
} else if (type == .f16x2) {
    fA[0] = a[0:15];
    fA[1] = a[16:31];
    fB[0] = b[0:15];
    fB[1] = b[16:31];
    t[0] = (fA[0] CmpOp fB[0]) ? 1 : 0;
    t[1] = (fA[1] CmpOp fB[1]) ? 1 : 0;
    for (i = 0; i < 2; i++) {
         d[i] = BoolOp(t[i], c) ? 1.0 : 0.0;
    }
}
Floating Point Notes

The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is NaN, the result is False.

To aid comparison operations in the presence of NaN values, unordered versions are included: equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not NaN), then these comparisons have the same result as their ordered counterparts. If either operand is NaN, then the result of these comparisons is True.

num returns True if both operands are numeric values (not NaN), and nan returns True if either operand is NaN.

Subnormal numbers:

By default, subnormal numbers are supported.

set.ftz.{f16,f16x2}.{f16,f16x2,f32} flushes subnormal inputs to sign-preserving zero.

PTX ISA Notes

Introduced in PTX ISA version 4.2.

Target ISA Notes

Requires sm_53 or higher.

Examples
   set.lt.and.f16.f16  d,a,b,r;
   set.eq.f16x2.f16x2  d,i,n;

9.7.6.2. Half Precision Comparison Instructions: setp

setp

Compare two numeric values with a relational operator, and optionally combine this result with a predicate value by applying a Boolean operator.

Syntax
setp.CmpOp{.ftz}.f16           p, a, b;
setp.CmpOp.BoolOp{.ftz}.f16    p, a, b, {!}c;

setp.CmpOp{.ftz}.f16x2         p|q, a, b;
setp.CmpOp.BoolOp{.ftz}.f16x2  p|q, a, b, {!}c;

.CmpOp  = { eq, ne, lt, le, gt, ge,
            equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
Description

Compares two values and combines the result with another predicate value by applying a Boolean operator. This result is written to the destination operand.

Operand c, p and q has type .pred.

For instruction type .f16, operands a and b have type .b16 or .f16

For instruction type .f16x2, operands a and b have type .b32

Semantics
if (type == .f16) {
     t = (a CmpOp b) ? 1 : 0;
     p = BoolOp(t, c);
} else if (type == .f16x2) {
    fA[0] = a[0:15];
    fA[1] = a[16:31];
    fB[0] = b[0:15];
    fB[1] = b[16:31];
    t[0] = (fA[0] CmpOp fB[0]) ? 1 : 0;
    t[1] = (fA[1] CmpOp fB[1]) ? 1 : 0;
    p = BoolOp(t[0], c);
    q = BoolOp(t[1], c);
}
Floating Point Notes

The ordered comparisons are eq, ne, lt, le, gt, ge. If either operand is NaN, the result is False.

To aid comparison operations in the presence of NaN values, unordered versions are included: equ, neu, ltu, leu, gtu, geu. If both operands are numeric values (not NaN), then these comparisons have the same result as their ordered counterparts. If either operand is NaN, then the result of these comparisons is True.

num returns True if both operands are numeric values (not NaN), and nan returns True if either operand is NaN.

Subnormal numbers:

By default, subnormal numbers are supported.

setp.ftz.{f16,f16x2} flushes subnormal inputs to sign-preserving zero.

PTX ISA Notes

Introduced in PTX ISA version 4.2.

Target ISA Notes

Requires sm_53 or higher.

Examples
    setp.lt.and.f16x2  p|q,a,b,r;
    @q  setp.eq.f16        p,i,n;

9.7.7. Logic and Shift Instructions

The logic and shift instructions are fundamentally untyped, performing bit-wise operations on operands of any type, provided the operands are of the same size. This permits bit-wise operations on floating point values without having to define a union to access the bits. Instructions and, or, xor, and not also operate on predicates.

The logical shift instructions are:
  • and
  • or
  • xor
  • not
  • cnot
  • lop3
  • shf
  • shl
  • shr

9.7.7.1. Logic and Shift Instructions: and

and

Bitwise AND.

Syntax
and.type d, a, b;

.type = { .pred, .b16, .b32, .b64 };
Description

Compute the bit-wise and operation for the bits in a and b.

Semantics
d = a & b;
Notes

The size of the operands must match, but not necessarily the type.

Allowed types include predicate registers.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    and.b32  x,q,r;    
    and.b32  sign,fpvalue,0x80000000;

9.7.7.2. Logic and Shift Instructions: or

or

Biwise OR.

Syntax
or.type d, a, b;

.type = { .pred, .b16, .b32, .b64 };
Description

Compute the bit-wise or operation for the bits in a and b.

Semantics
d = a | b;
Notes

The size of the operands must match, but not necessarily the type.

Allowed types include predicate registers.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    or.b32  mask mask,0x00010001
    or.pred  p,q,r;

9.7.7.3. Logic and Shift Instructions: xor

xor

Bitwise exclusive-OR (inequality).

Syntax
xor.type d, a, b;

.type = { .pred, .b16, .b32, .b64 };
Description

Compute the bit-wise exclusive-or operation for the bits in a and b.

Semantics
d = a ^ b;
Notes

The size of the operands must match, but not necessarily the type.

Allowed types include predicate registers.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    xor.b32  d,q,r;
    xor.b16  d,x,0x0001;

9.7.7.4. Logic and Shift Instructions: not

not

Bitwise negation; one's complement.

Syntax
not.type d, a;

.type = { .pred, .b16, .b32, .b64 };
Description

Invert the bits in a.

Semantics
d = ~a;
Notes

The size of the operands must match, but not necessarily the type.

Allowed types include predicates.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    not.b32  mask,mask;
    not.pred  p,q;

9.7.7.5. Logic and Shift Instructions: cnot

cnot

C/C++ style logical negation.

Syntax
cnot.type d, a;

.type = { .b16, .b32, .b64 };
Description

Compute the logical negation using C/C++ semantics.

Semantics
d = (a==0) ? 1 : 0;
Notes

The size of the operands must match, but not necessarily the type.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    cnot.b32 d,a;

9.7.7.6. Logic and Shift Instructions: lop3

lop3

Arbitrary logical operation on 3 inputs

Syntax
lop3.b32 d, a, b, c, immLut;
Description

Compute logical operation on inputs a, b, c and stores result in destination d.

Logical operation to be performed is specified by immLut operand which is an integer constant from 0 to 255.

Possible logical operations involving 3 inputs is 256 as shown in following table and immLut specifies the operation to perform on inputs a, b, c.

ta tb tc Oper 0 (False) Oper 1 (ta & tb & tc) Oper 2 (ta & tb & ~tc) ... Oper 254 (ta | tb | tc) Oper 255 (True)
0 0 0 0 0 0 ... 0 1
0 0 1 0 0 0 1 1
0 1 0 0 0 0 1 1
0 1 1 0 0 0 1 1
1 0 0 0 0 0 1 1
1 0 1 0 0 0 1 1
1 1 0 0 0 1 1 1
1 1 1 0 1 0 1 1
immLut 0x0 0x80 0x40 ... 0xFE 0xFF

immLut value is computed by applying required operation on input values in above 3 input table. 

ta = 0xF0;   // Value corresponding to column “ta” in above table
tb = 0xCC;   // Value corresponding to column “tb” in above table
tc = 0xAA;   // Value corresponding to column “tc” in above table
immLut = F(ta, tb, tc);

Example:

    If F = (a & b & c);
    immLut = 0xF0 & 0xCC & 0xAA = 0x80

    If F = (a | b | c);
    immLut = 0xF0 | 0xCC | 0xAA = 0xFE

    If F = (a & b & ~c);
    immLut = 0xF0 & 0xCC & (~0xAA) = 0x40

    If F = ((a & b | c) ^ a);
    immLut = (0xF0 & 0xCC | 0xAA) ^ 0xF0 = 0xAB
Semantics
F = GetFunctionFromTable(immLut); // returns the function corresponding to immLut value
d = F(a, b, c);
PTX ISA Notes

Introduced in PTX ISA version 4.3.

Target ISA Notes

Requires sm_50 or higher.

Examples
    lop3.b32  d, a, b, c, 0x40;

9.7.7.7. Logic and Shift Instructions: shf

shf

Funnel shift.

Syntax
shf.l.mode.b32  d, a, b, c;  // left shift
shf.r.mode.b32  d, a, b, c;  // right shift

.mode = { .clamp, .wrap };
Description

Shift the 64-bit value formed by concatenating operands a and b left or right by the amount specified by the unsigned 32-bit value in c. Operand b holds bits 63:32 and operand a holds bits 31:0 of the 64-bit source value. The source is shifted left or right by the clamped or wrapped value in c. For shf.l, the most-significant 32-bits of the result are written into d; for shf.r, the least-significant 32-bits of the result are written into d.

Semantics
u32  n = (.mode == .clamp) ? min(c, 32) : c & 0x1f;
switch (shf.dir) {  // shift concatenation of [b, a]
    case shf.l:     // extract 32 msbs
           u32  d = (b << n)      | (a >> (32-n));
    case shf.r:     // extract 32 lsbs
           u32  d = (b << (32-n)) | (a >> n);
}
Notes

Use funnel shift for multi-word shift operations and for rotate operations. The shift amount is limited to the range 0..32 in clamp mode and 0..31 in wrap mode, so shifting multi-word values by distances greater than 32 requires first moving 32-bit words, then using shf to shift the remaining 0..31 distance.

To shift data sizes greater than 64 bits to the right, use repeated shf.r instructions applied to adjacent words, operating from least-significant word towards most-significant word. At each step, a single word of the shifted result is computed. The most-significant word of the result is computed using a shr.{u32,s32} instruction, which zero or sign fills based on the instruction type.

To shift data sizes greater than 64 bits to the left, use repeated shf.l instructions applied to adjacent words, operating from most-significant word towards least-significant word. At each step, a single word of the shifted result is computed. The least-significant word of the result is computed using a shl instruction.

Use funnel shift to perform 32-bit left or right rotate by supplying the same value for source arguments a and b.

PTX ISA Notes

Introduced in PTX ISA version 3.1.

Target ISA Notes

Requires sm_32 or higher.

Example
    shf.l.clamp.b32  r3,r1,r0,16;

    // 128-bit left shift; n < 32
    // [r7,r6,r5,r4] = [r3,r2,r1,r0] << n
    shf.l.clamp.b32  r7,r2,r3,n;
    shf.l.clamp.b32  r6,r1,r2,n;
    shf.l.clamp.b32  r5,r0,r1,n;
    shl.b32          r4,r0,n;

    // 128-bit right shift, arithmetic; n < 32
    // [r7,r6,r5,r4] = [r3,r2,r1,r0] >> n
    shf.r.clamp.b32  r4,r0,r1,n;
    shf.r.clamp.b32  r5,r1,r2,n;
    shf.r.clamp.b32  r6,r2,r3,n;
    shr.s32          r7,r3,n;     // result is sign-extended

    shf.r.clamp.b32  r1,r0,r0,n;  // rotate right by n; n < 32
    shf.l.clamp.b32  r1,r0,r0,n;  // rotate left by n; n < 32

    // extract 32-bits from [r1,r0] starting at position n < 32
    shf.r.clamp.b32  r0,r0,r1,n;

9.7.7.8. Logic and Shift Instructions: shl

shl

Shift bits left, zero-fill on right.

Syntax
shl.type d, a, b;

.type = { .b16, .b32, .b64 };
Description

Shift a left by the amount specified by unsigned 32-bit value in b.

Semantics
d = a << b;
Notes

Shift amounts greater than the register width N are clamped to N.

The sizes of the destination and first source operand must match, but not necessarily the type. The b operand must be a 32-bit value, regardless of the instruction type.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Example
    shl.b32  q,a,2;

9.7.7.9. Logic and Shift Instructions: shr

shr

Shift bits right, sign or zero-fill on left.

Syntax
shr.type d, a, b;

.type = { .b16, .b32, .b64,
          .u16, .u32, .u64,
          .s16, .s32, .s64 };
Description

Shift a right by the amount specified by unsigned 32-bit value in b. Signed shifts fill with the sign bit, unsigned and untyped shifts fill with 0.

Semantics
d = a >> b;
Notes

Shift amounts greater than the register width N are clamped to N.

The sizes of the destination and first source operand must match, but not necessarily the type. The b operand must be a 32-bit value, regardless of the instruction type.

Bit-size types are included for symmetry with shl.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Example
    shr.u16  c,a,2;
    shr.s32  i,i,1;
    shr.b16  k,i,j;

9.7.8. Data Movement and Conversion Instructions

These instructions copy data from place to place, and from state space to state space, possibly converting it from one format to another. mov, ld, ldu, and st operate on both scalar and vector types. The isspacep instruction is provided to query whether a generic address falls within a particular state space window. The cvta instruction converts addresses between generic and const, global, local, or shared state spaces.

Instructions ld, st, suld, and sust support optional cache operations.

The Data Movement and Conversion Instructions are:
  • mov
  • shfl
  • prmt
  • ld
  • ldu
  • st
  • prefetch, prefetchu
  • isspacep
  • cvta
  • cvt

9.7.8.1. Cache Operators

PTX ISA version 2.0 introduced optional cache operators on load and store instructions. The cache operators require a target architecture of sm_20 or higher.

Cache operators on load or store instructions are treated as performance hints only. The use of a cache operator on an ld or st instruction does not change the memory consistency behavior of the program.

For sm_20 and higher, the cache operators have the following definitions and behavior.

Table 27. Cache Operators for Memory Load Instructions
Operator Meaning
.ca

Cache at all levels, likely to be accessed again.

The default load instruction cache operation is ld.ca, which allocates cache lines in all levels (L1 and L2) with normal eviction policy. Global data is coherent at the L2 level, but multiple L1 caches are not coherent for global data. If one thread stores to global memory via one L1 cache, and a second thread loads that address via a second L1 cache with ld.ca, the second thread may get stale L1 cache data, rather than the data stored by the first thread. The driver must invalidate global L1 cache lines between dependent grids of parallel threads. Stores by the first grid program are then correctly fetched by the second grid program issuing default ld.ca loads cached in L1.

.cg

Cache at global level (cache in L2 and below, not L1).

Use ld.cg to cache loads only globally, bypassing the L1 cache, and cache only in the L2 cache.

.cs

Cache streaming, likely to be accessed once.

The ld.cs load cached streaming operation allocates global lines with evict-first policy in L1 and L2 to limit cache pollution by temporary streaming data that may be accessed once or twice. When ld.cs is applied to a Local window address, it performs the ld.lu operation.

.lu

Last use.

The compiler/programmer may use ld.lu when restoring spilled registers and popping function stack frames to avoid needless write-backs of lines that will not be used again. The ld.lu instruction performs a load cached streaming operation (ld.cs) on global addresses.

.cv

Don't cache and fetch again (consider cached system memory lines stale, fetch again).

The ld.cv load operation applied to a global System Memory address invalidates (discards) a matching L2 line and re-fetches the line on each new load.

Table 28. Cache Operators for Memory Store Instructions
Operator Meaning
.wb

Cache write-back all coherent levels.

The default store instruction cache operation is st.wb, which writes back cache lines of coherent cache levels with normal eviction policy.

If one thread stores to global memory, bypassing its L1 cache, and a second thread in a different SM later loads from that address via a different L1 cache with ld.ca, the second thread may get a hit on stale L1 cache data, rather than get the data from L2 or memory stored by the first thread.

The driver must invalidate global L1 cache lines between dependent grids of thread arrays. Stores by the first grid program are then correctly missed in L1 and fetched by the second grid program issuing default ld.ca loads.

.cg

Cache at global level (cache in L2 and below, not L1).

Use st.cg to cache global store data only globally, bypassing the L1 cache, and cache only in the L2 cache.

.cs

Cache streaming, likely to be accessed once.

The st.cs store cached-streaming operation allocates cache lines with evict-first policy to limit cache pollution by streaming output data.

.wt

Cache write-through (to system memory).

The st.wt store write-through operation applied to a global System Memory address writes through the L2 cache.

9.7.8.2. Data Movement and Conversion Instructions: mov

mov

Set a register variable with the value of a register variable or an immediate value. Take the non-generic address of a variable in global, local, or shared state space.

Syntax
mov.type  d, a;
mov.type  d, sreg;
mov.type  d, avar;       // get address of variable
mov.type  d, avar+imm;   // get address of variable with offset
mov.type  d, label;      // get address of label
mov.type  d, fname;      // get address of device function
mov.u64   d, kernel;     // get address of entry function

.type = { .pred,
          .b16, .b32, .b64,
          .u16, .u32, .u64,
          .s16, .s32, .s64,
                .f32, .f64 };
Description

Write register d with the value of a.

Operand a may be a register, special register, variable with optional offset in an addressable memory space, label, or function name.

For variables declared in .const, .global, .local, and .shared state spaces, mov places the non-generic address of the variable (i.e., the address of the variable in its state space) into the destination register. The generic address of a variable in const, global, local, or shared state space may be generated by first taking the address within the state space with mov and then converting it to a generic address using the cvta instruction; alternately, the generic address of a variable declared in const, global, local, or shared state space may be taken directly using the cvta instruction.

Note that if the address of a device function parameter is moved to a register, the parameter will be copied onto the stack and the address will be in the local state space.

Semantics
d = a;
d = sreg;
d = &avar;        // address is non-generic; i.e., within the variable's declared state space
d = &avar+imm;
d = &label;
Notes

Although only predicate and bit-size types are required, we include the arithmetic types for the programmer's convenience: their use enhances program readability and allows additional type checking.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Taking the address of kernel entry functions requires PTX ISA version 3.1 or later. Kernel function addresses should only be used in the context of CUDA Dynamic Parallelism system calls. See the CUDA Dynamic Parallelism Programming Guide for details.

Target ISA Notes

mov.f64 requires sm_13 or higher.

Taking the address of kernel entry functions requires sm_35 or higher.

Examples
    mov.f32  d,a;
    mov.u16  u,v;
    mov.f32  k,0.1;
    mov.u32  ptr, A;        // move address of A into ptr
    mov.u32  ptr, A[5];     // move address of A[5] into ptr
    mov.u32  ptr, A+20;     // move address with offset into ptr
    mov.u32  addr, myFunc;  // get address of device function 'myFunc'
    mov.u64  kptr, main;    // get address of entry function 'main'

9.7.8.3. Data Movement and Conversion Instructions: mov

mov

Move vector-to-scalar (pack) or scalar-to-vector (unpack).

Syntax
mov.type  d, a;

.type = { .b16, .b32, .b64 };
Description

Write scalar register d with the packed value of vector register a, or write vector register d with the unpacked values from scalar register a.

For bit-size types, mov may be used to pack vector elements into a scalar register or unpack sub-fields of a scalar register into a vector. Both the overall size of the vector and the size of the scalar must match the size of the instruction type.

Semantics
// pack two 8-bit elements into .b16
d = a.x | (a.y << 8)
// pack four 8-bit elements into .b32
d = a.x | (a.y << 8)  | (a.z << 16) | (a.w << 24)
// pack two 16-bit elements into .b32
d = a.x | (a.y << 16)
// pack four 16-bit elements into .b64
d = a.x | (a.y << 16)  | (a.z << 32) | (a.w << 48)
// pack two 32-bit elements into .b64
d = a.x | (a.y << 32)

// unpack 8-bit elements from .b16
{ d.x, d.y } = { a[0..7], a[8..15] }
// unpack 8-bit elements from .b32
{ d.x, d.y, d.z, d.w } 
        { a[0..7], a[8..15], a[16..23], a[24..31] }

// unpack 16-bit elements from .b32
{ d.x, d.y }  = { a[0..15], a[16..31] }
// unpack 16-bit elements from .b64
{ d.x, d.y, d.z, d.w } =
        { a[0..15], a[16..31], a[32..47], a[48..63] }
 
// unpack 32-bit elements from .b64
{ d.x, d.y } = { a[0..31], a[32..63] }
PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    mov.b32 %r1,{a,b};      // a,b have type .u16
    mov.b64 {lo,hi}, %x;    // %x is a double; lo,hi are .u32
    mov.b32 %r1,{x,y,z,w};  // x,y,z,w have type .b8
    mov.b32 {r,g,b,a},%r1;  // r,g,b,a have type .u8

9.7.8.4. Data Movement and Conversion Instructions: shfl

shfl

Register data shuffle within threads of a warp.

Syntax
shfl.mode.b32  d[|p], a, b, c;

.mode = { .up, .down, .bfly, .idx };
Description

Exchange register data between threads of a warp.

Each thread in the currently executing warp will compute a source lane index j based on input operands b and c and the mode. If the computed source lane index j is in range, the thread will copy the input operand a from lane j into its own destination register d; otherwise, the thread will simply copy its own input a to destination d. The optional destination predicate p is set to True if the computed source lane is in range, and otherwise set to False.

Note that an out of range value of b may still result in a valid computed source lane index j. In this case, a data transfer occurs and the destination predicate p is True.

Note that results are undefined in divergent control flow within a warp, if an active thread sources a register from an inactive thread.

Operand b specifies a source lane or source lane offset, depending on the mode.

Operand c contains two packed values specifying a mask for logically splitting warps into sub-segments and an upper bound for clamping the source lane index.

Semantics
lane[4:0]  = [Thread].laneid;  // position of thread in warp
bval[4:0] = b[4:0];            // source lane or lane offset (0..31)
cval[4:0] = c[4:0];            // clamp value
mask[4:0] = c[12:8];

// get value of source register a if thread is active and
// guard predicate true, else unpredictable
if (isActive(Thread) && isGuardPredicateTrue(Thread)) {
    SourceA[lane] = a;
} else {
    // Value of SourceA[lane] is unpredictable for
    // inactive/predicated-off threads in warp
}
maxLane = (lane[4:0] & mask[4:0]) | (cval[4:0] & ~mask[4:0]);
minLane = (lane[4:0] & mask[4:0]);

switch (.mode) {
    case .up:    j = lane - bval; pval = (j >= maxLane); break;
    case .down:  j = lane + bval; pval = (j <= maxLane); break;
    case .bfly:  j = lane ^ bval; pval = (j <= maxLane); break;
    case .idx:   j = minLane  | (bval[4:0] & ~mask[4:0]);
                                 pval = (j <= maxLane); break;
}
if (!pval) j = lane;  // copy from own lane
d = SourceA[j];       // copy input a from lane j
if (dest predicate selected)
    p = pval;
PTX ISA Notes

Introduced in PTX ISA version 3.0.

Target ISA Notes

shfl requires sm_30 or higher.

Examples
    // Warp-level INCLUSIVE PLUS SCAN:
    //
    // Assumes input in following registers:
    //     - Rx  = sequence value for this thread
    //
    shfl.up.b32  Ry|p, Rx, 0x1,  0x0;
@p  add.f32      Rx, Ry, Rx;
    shfl.up.b32  Ry|p, Rx, 0x2,  0x0;
@p  add.f32      Rx, Ry, Rx;
    shfl.up.b32  Ry|p, Rx, 0x4,  0x0;
@p  add.f32      Rx, Ry, Rx;
    shfl.up.b32  Ry|p, Rx, 0x8,  0x0;
@p  add.f32      Rx, Ry, Rx;
    shfl.up.b32  Ry|p, Rx, 0x10, 0x0;
@p  add.f32      Rx, Ry, Rx;


    // Warp-level INCLUSIVE PLUS REVERSE-SCAN:
    //
    // Assumes input in following registers:
    //     - Rx  = sequence value for this thread
    //
    shfl.down.b32  Ry|p, Rx, 0x1,  0x1f;
@p  add.f32        Rx, Ry, Rx;
    shfl.down.b32  Ry|p, Rx, 0x2,  0x1f;
@p  add.f32        Rx, Ry, Rx;
    shfl.down.b32  Ry|p, Rx, 0x4,  0x1f;
@p  add.f32        Rx, Ry, Rx;
    shfl.down.b32  Ry|p, Rx, 0x8,  0x1f;
@p  add.f32        Rx, Ry, Rx;
    shfl.down.b32  Ry|p, Rx, 0x10, 0x1f;
@p  add.f32        Rx, Ry, Rx;


    // BUTTERFLY REDUCTION:
    //
    // Assumes input in following registers:
    //     - Rx  = sequence value for this thread
    //
    shfl.bfly.b32  Ry, Rx, 0x10, 0x1f;   // no predicate dest
    add.f32        Rx, Ry, Rx;
    shfl.bfly.b32  Ry, Rx, 0x8,  0x1f;
    add.f32        Rx, Ry, Rx;
    shfl.bfly.b32  Ry, Rx, 0x4,  0x1f;
    add.f32        Rx, Ry, Rx;
    shfl.bfly.b32  Ry, Rx, 0x2,  0x1f;
    add.f32        Rx, Ry, Rx;
    shfl.bfly.b32  Ry, Rx, 0x1,  0x1f;
    add.f32        Rx, Ry, Rx;
    //
    // All threads now hold sum in Rx

9.7.8.5. Data Movement and Conversion Instructions: shfl.sync

shfl.sync

Register data shuffle within threads of a warp.

Syntax
shfl.sync.mode.b32  d[|p], a, b, c, membermask;

.mode = { .up, .down, .bfly, .idx };
Description

Exchange register data between threads of a warp.

shfl.sync will cause executing thread to wait until all threads corresponding to membermask have executed shfl.sync with the same qualifiers and same membermask value before resuming execution.

Operand membermask specifies a 32-bit integer which is a mask indicating threads participating in barrier where the bit position corresponds to thread’s laneid.

shfl.sync exchanges register data between threads in membermask.

Each thread in the currently executing warp will compute a source lane index j based on input operands b and c and the mode. If the computed source lane index j is in range, the thread will copy the input operand a from lane j into its own destination register d; otherwise, the thread will simply copy its own input a to destination d. The optional destination predicate p is set to True if the computed source lane is in range, and otherwise set to False.

Note that an out of range value of b may still result in a valid computed source lane index j. In this case, a data transfer occurs and the destination predicate p is True.

Note that results are undefined if a thread sources a register from a thread that is not in membermask.

Operand b specifies a source lane or source lane offset, depending on the mode.

Operand c contains two packed values specifying a mask for logically splitting warps into sub-segments and an upper bound for clamping the source lane index.

The behavior of shfl.sync is undefined if the executing thread is not in the membermask.

Note: For .target sm_6x or below, all threads in membermask must execute the same shfl.sync instruction in convergence, and only threads belonging to some membermask can be active when the shfl.sync instruction is executed. Otherwise, the behavior is undefined.
Semantics
// wait for all threads in membermask to arrive
wait_for_specified_threads(membermask);

lane[4:0]  = [Thread].laneid;  // position of thread in warp
bval[4:0] = b[4:0];            // source lane or lane offset (0..31)
cval[4:0] = c[4:0];            // clamp value
segmask[4:0] = c[12:8];

// get value of source register a if thread is active and
// guard predicate true, else unpredictable
if (isActive(Thread) && isGuardPredicateTrue(Thread)) {
    SourceA[lane] = a;
} else {
    // Value of SourceA[lane] is unpredictable for
    // inactive/predicated-off threads in warp
}
maxLane = (lane[4:0] & segmask[4:0]) | (cval[4:0] & ~segmask[4:0]);
minLane = (lane[4:0] & segmask[4:0]);

switch (.mode) {
    case .up:    j = lane - bval; pval = (j >= maxLane); break;
    case .down:  j = lane + bval; pval = (j <= maxLane); break;
    case .bfly:  j = lane ^ bval; pval = (j <= maxLane); break;
    case .idx:   j = minLane  | (bval[4:0] & ~segmask[4:0]);
                                 pval = (j <= maxLane); break;
}
if (!pval) j = lane;  // copy from own lane
d = SourceA[j];       // copy input a from lane j
if (dest predicate selected)
    p = pval;
PTX ISA Notes

Introduced in PTX ISA version 6.0.

Target ISA Notes

Requires sm_30 or higher.

Examples
    shfl.sync.up.b32  Ry|p, Rx, 0x1,  0x0, 0xffffffff;

9.7.8.6. Data Movement and Conversion Instructions: prmt

prmt

Permute bytes from register pair.

Syntax
prmt.b32{.mode}  d, a, b, c;

.mode = { .f4e, .b4e, .rc8, .ecl, .ecr, .rc16 };
Description

Pick four arbitrary bytes from two 32-bit registers, and reassemble them into a 32-bit destination register.

In the generic form (no mode specified), the permute control consists of four 4-bit selection values. The bytes in the two source registers are numbered from 0 to 7: {b, a} = {{b7, b6, b5, b4}, {b3, b2, b1, b0}}. For each byte in the target register, a 4-bit selection value is defined.

The 3 lsbs of the selection value specify which of the 8 source bytes should be moved into the target position. The msb defines if the byte value should be copied, or if the sign (msb of the byte) should be replicated over all 8 bits of the target position (sign extend of the byte value); msb=0 means copy the literal value; msb=1 means replicate the sign. Note that the sign extension is only performed as part of generic form.

Thus, the four 4-bit values fully specify an arbitrary byte permute, as a 16b permute code.

default mode

d.b3

source select

d.b2

source select

d.b1

source select

d.b0

source select
index c[15:12] c[11:8] c[7:4] c[3:0]

The more specialized form of the permute control uses the two lsb's of operand c (which is typically an address pointer) to control the byte extraction.

mode

selector

c[1:0]

d.b3

source

d.b2

source

d.b1

source

d.b0

source
f4e (forward 4 extract) 0 3 2 1 0
  1 4 3 2 1
  2 5 4 3 2
  3 6 5 4 3
b4e (backward 4 extract) 0 5 6 7 0
  1 6 7 0 1
  2 7 0 1 2
  3 0 1 2 3
rc8 (replicate 8) 0 0 0 0 0
  1 1 1 1 1
  2 2 2 2 2
  3 3 3 3 3
ecl (edge clamp left) 0 3 2 1 0
  1 3 2 1 1
  2 3 2 2 2
  3 3 3 3 3
ecr (edge clamp right) 0 0 0 0 0
  1 1 1 1 0
  2 2 2 1 0
  3 3 2 1 0
rc16 (replicate 16) 0 1 0 1 0
  1 3 2 3 2
  2 1 0 1 0
  3 3 2 3 2
Semantics
tmp64 = (b<<32) | a;  // create 8 byte source

if ( ! mode ) {
   ctl[0] = (c >>  0) & 0xf;
   ctl[1] = (c >>  4) & 0xf;
   ctl[2] = (c >>  8) & 0xf;
   ctl[3] = (c >> 12) & 0xf;
} else {
   ctl[0] = ctl[1] = ctl[2] = ctl[3] = (c >>  0) & 0x3;
}

tmp[07:00] = ReadByte( mode, ctl[0], tmp64 );
tmp[15:08] = ReadByte( mode, ctl[1], tmp64 );
tmp[23:16] = ReadByte( mode, ctl[2], tmp64 );
tmp[31:24] = ReadByte( mode, ctl[3], tmp64 );
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

prmt requires sm_20 or higher.

Examples
    prmt.b32      r1, r2, r3, r4;
    prmt.b32.f4e  r1, r2, r3, r4;

9.7.8.7. Data Movement and Conversion Instructions: ld

ld

Load a register variable from an addressable state space variable.

Syntax
ld{.weak}{.ss}{.cop}{.vec}.type d, [a];
ld.volatile{.ss}{.vec}.type d, [a];
ld.relaxed.scope{.ss}{.vec}.type d, [a];
ld.acquire.scope{.ss}{.vec}.type d, [a];

.ss =    {.const, .global, .local, .param, .shared};
.cop =   {.ca, .cg, .cs, .lu, .cv};
.scope = {.cta, .gpu, .sys};
.vec =   { .v2, .v4 };
.type =  { .b8, .b16, .b32, .b64,
           .u8, .u16, .u32, .u64,
           .s8, .s16, .s32, .s64,
           .f32, .f64 };
Description

Load register variable d from the location specified by the source address operand a in specified state space. If no state space is given, perform the load using Generic Addressing.

Supported addressing modes for operand a are described in Addresses as Operands

Instruction ld.param used for reading value returned from device function call cannot be predicated. See Parameter State Space and Function Declarations and Definitions for descriptions of the proper use of ld.param.

The .relaxed and .acquire qualifiers indicate memory synchronization as described in the Memory Consistency Model. The .scope qualifier indicates the set of threads with which an ld.relaxed or ld.acquire instruction can directly synchronize1. The .weak qualifier indicates a memory instruction with no synchronization. The effects of this instruction become visible to other threads only when synchronization is established by other means.

The .weak, .volatile, .relaxed and .acquire qualifiers are mutually exclusive. When none of these is specified, the .weak qualifier is assumed by default.

An ld.volatile operation is always performed and it will not be reordered with respect to other volatile operations to the same memory location. volatile and non-volatile load operations to the same memory location may be reordered.ld.volatile has the same memory synchronization semantics as ld.relaxed.sys.

The qualifiers .volatile, .relaxed and .acquire may be used only with .global and .shared spaces and with generic addressing, where the address points to .global or .shared space. Cache operations are not permitted with these qualifiers.

1 This synchronization is further extended to other threads through the transitive nature of causality order, as described in the memory consistency model.

Semantics
d = a;             // named variable a
d = *(&a+immOff)   // variable-plus-offset
d = *a;            // register
d = *(a+immOff);   // register-plus-offset
d = *(immAddr);    // immediate address
Notes

Destination d must be in the .reg state space.

A destination register wider than the specified type may be used. The value loaded is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned and bit-size types. See Table 25 for a description of these relaxed type-checking rules.

.f16 data may be loaded using ld.b16, and then converted to .f32 or .f64 using cvt or can be used in half precision floating point instructions.

.f16x2 data may be loading using ld.b32 and then used in half precision floating point instructions.

PTX ISA Notes

ld introduced in PTX ISA version 1.0. ld.volatile introduced in PTX ISA version 1.1.

Generic addressing and cache operations introduced in PTX ISA version 2.0.

Support for scope qualifier, .relaxed, .acquire, .weak qualifiers introduced in PTX ISA version 6.0.

Support for generic addressing of .const space added in PTX ISA version 3.1.

Target ISA Notes

ld.f64 requires sm_13 or higher.

Support for scope qualifier, .relaxed, .acquire, .weak qualifiers require sm_70 or higher.

Generic addressing requires sm_20 or higher.

Cache operations require sm_20 or higher.

Examples
    ld.global.f32    d,[a];
    ld.shared.v4.b32 Q,[p];
    ld.const.s32     d,[p+4];
    ld.local.b32     x,[p+-8]; // negative offset
    ld.local.b64     x,[240];  // immediate address

    ld.global.b16    %r,[fs];  // load .f16 data into 32-bit reg
    cvt.f32.f16      %r,%r;    // up-convert f16 data to f32

    ld.global.b32    %r0, [fs];     // load .f16x2 data in 32-bit reg
    ld.global.b32    %r1, [fs + 4]; // load .f16x2 data in 32-bit reg
    add.rn.f16x2     %d0, %r0, %r1; // addition of f16x2 data
    
    ld.global.relaxed.gpu.u32 %r0, [gbl];
    ld.shared.acquire.gpu.u32 %r1, [sh];

9.7.8.8. Data Movement and Conversion Instructions: ld.global.nc

ld.global.nc

Load a register variable from global state space via non-coherent cache.

Syntax
ld.global{.cop}.nc.type      d, [a];
ld.global{.cop}.nc.vec.type  d, [a];

.cop  = { .ca, .cg, .cs };     // cache operation
.vec  = { .v2, .v4 };
.type = { .b8, .b16, .b32, .b64,
          .u8, .u16, .u32, .u64,
          .s8, .s16, .s32, .s64,
                     .f32, .f64 };
Description

Load register variable d from the location specified by the source address operand a in the global state space, and optionally cache in non-coherent texture cache. Since the cache is non-coherent, the data should be read-only within the kernel's process.

The texture cache is larger, has higher bandwidth, and longer latency than the global memory cache. For applications with sufficient parallelism to cover the longer latency, ld.global.nc should offer better performance than ld.global.

Supported addressing modes for operand a are described in Addresses as Operands

Semantics
d = a;             // named variable a
d = *(&a+immOff)   // variable-plus-offset
d = *a;            // register
d = *(a+immOff);   // register-plus-offset
d = *(immAddr);    // immediate address
Notes

Destination d must be in the .reg state space.

A destination register wider than the specified type may be used. The value loaded is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned and bit-size types.

.f16 data may be loaded using ld.b16, and then converted to .f32 or .f64 using cvt.

PTX ISA Notes

Support for generic addressing of .const space added in PTX ISA version 3.1.

Target ISA Notes

Requires sm_32 or higher.

Examples
    ld.global.nc.f32  d,[a];

9.7.8.9. Data Movement and Conversion Instructions: ldu

ldu

Load read-only data from an address that is common across threads in the warp.

Syntax
ldu{.ss}.type      d, [a];       // load from address
ldu{.ss}.vec.type  d, [a];       // vec load from address

.ss   = { .global };             // state space
.vec  = { .v2, .v4 };
.type = { .b8, .b16, .b32, .b64,
           .u8, .u16, .u32, .u64,
           .s8, .s16, .s32, .s64,
                      .f32, .f64 };
Description

Load read-only data into register variable d from the location specified by the source address operand a in the global state space, where the address is guaranteed to be the same across all threads in the warp. If no state space is given, perform the load using Generic Addressing.

Supported addressing modes for operand a are described in Addresses as Operands

Semantics
d = a;             // named variable a
d = *(&a+immOff)   // variable-plus-offset
d = *a;            // register
d = *(a+immOff);   // register-plus-offset
d = *(immAddr);    // immediate address
Notes

Destination d must be in the .reg state space.

A destination register wider than the specified type may be used. The value loaded is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned and bit-size types. See Table 25 for a description of these relaxed type-checking rules.

.f16 data may be loaded using ldu.b16, and then converted to .f32 or .f64 using cvt or can be used in half precision floating point instructions.

f16x2 data may be loading using ldu.b32 and then used in half precision floating point instructions.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

ldu.f64 requires sm_13 or higher.

Examples
    ldu.global.f32    d,[a];
    ldu.global.b32    d,[p+4];
    ldu.global.v4.f32 Q,[p];

9.7.8.10. Data Movement and Conversion Instructions: st

st

Store a register variable to an addressable state space variable.

Syntax
st{.weak}{.ss}{.cop}{.vec}.type [a], b;
st.volatile{.ss}{.vec}.type [a], b;
st.relaxed.scope{.ss}{.vec}.scope.type [a], b;
st.release.scope{.ss}{.vec}.scope.type [a], b;

.ss =    {.global, .local, .param, .shared };
.cop =   { .wb, .cg, .cs, .wt };
.sem =   {.relaxed, .release};
.scope = {.cta, .gpu, .sys};
.vec =   { .v2, .v4 };
.type =  { .b8, .b16, .b32, .b64,
           .u8, .u16, .u32, .u64,
           .s8, .s16, .s32, .s64,
           .f32, .f64 };
Description

Store the value of register variable b in the location specified by the destination address operand a in specified state space. If no state space is given, perform the store using Generic Addressing. Stores to const memory are illegal.

Supported addressing modes for operand a are described in Addresses as Operands

Instruction st.param used for passing arguments to device function cannot be predicated. See Parameter State Space and Function Declarations and Definitions for descriptions of the proper use of st.param.

The qualifiers .relaxed and .release indicate memory synchronization as described in the Memory Consistency Model. The .scope qualifier indicates the set of threads with which an st.relaxed or st.release instruction can directly synchronize1. The .weak qualifier indicates a memory instruction with no synchronization. The effects of this instruction become visible to other threads only when synchronization is established by other means.

The .weak, .volatile, .relaxed and .release qualifiers are mutually exclusive. When none of these is specified, the .weak qualifier is assumed by default.

An st.volatile operation is always performed and it will not be reordered with respect to other volatile operations to the same memory location. st.volatile has the same memory synchronization semantics as st.relaxed.sys.

The qualifiers .volatile, .relaxed and .release may be used only with .global and .shared spaces and with generic addressing, where the address points to .global or .shared space. Cache operations are not permitted with these qualifiers.

1 This synchronization is further extended to other threads through the transitive nature of causality order, as described in the memory consistency model.

Semantics
d = a;                // named variable d
*(&a+immOffset) = b;            // variable-plus-offset
*a = b;               // register
*(a+immOffset) = b;   // register-plus-offset
*(immAddr) = b;       // immediate address
Notes

Operand b must be in the .reg state space.

A source register wider than the specified type may be used. The lower n bits corresponding to the instruction-type width are stored to memory. See Table 24 for a description of these relaxed type-checking rules.

.f16 data resulting from a cvt instruction may be stored using st.b16.

.f16x2 data may be stored using st.b32.

PTX ISA Notes

st introduced in PTX ISA version 1.0. st.volatile introduced in PTX ISA version 1.1.

Generic addressing and cache operations introduced in PTX ISA version 2.0.

Support for scope qualifier, .relaxed, .release, .weak qualifiers introduced in PTX ISA version 6.0.

Target ISA Notes

st.f64 requires sm_13 or higher.

Support for scope qualifier, .relaxed, .release, .weak qualifiers require sm_70 or higher.

Generic addressing requires sm_20 or higher.

Cache operations require sm_20 or higher.

Examples
    st.global.f32    [a],b;
    st.local.b32     [q+4],a;
    st.global.v4.s32 [p],Q;
    st.local.b32     [q+-8],a; // negative offset
    st.local.s32     [100],r7; // immediate address

    cvt.f16.f32      %r,%r;    // %r is 32-bit register
    st.b16           [fs],%r;  // store lower
    
    st.global.relaxed.sys.u32 [gbl], %r0;
    st.shared.release.cta.u32 [sh], %r1;

9.7.8.11. Data Movement and Conversion Instructions: prefetch, prefetchu

prefetch, prefetchu

Prefetch line containing a generic address at a specified level of memory hierarchy, in specified state space.

Syntax
prefetch{.space}.level  [a];   // prefetch to data cache
prefetchu.L1  [a];             // prefetch to uniform cache

.space = { .global, .local };
.level = { .L1, .L2 };
Description

The prefetch instruction brings the cache line containing the specified address in global or local memory state space into the specified cache level. If no state space is given, the prefetch uses Generic Addressing.

Supported addressing modes for operand a are described in Addresses as Operands

The prefetchu instruction brings the cache line containing the specified generic address into the specified uniform cache level.

A prefetch to a shared memory location performs no operation.

A prefetch into the uniform cache requires a generic address, and no operation occurs if the address maps to a const, local, or shared memory location.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

prefetch and prefetchu require sm_20 or higher.

Examples
    prefetch.global.L1  [ptr];
    prefetchu.L1  [addr];

9.7.8.12. Data Movement and Conversion Instructions: isspacep

isspacep

Query whether a generic address falls within a specified state space window.

Syntax
isspacep.space  p, a;    // result is .pred

.space = { const, .global, .local, .shared };
Description

Write predicate register p with 1 if generic address a falls within the specified state space window and with 0 otherwise. Destination p has type .pred; the source address operand must be of type .u32 or .u64.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

isspacep.const introduced in PTX ISA version 3.1.

Target ISA Notes

isspacep requires sm_20 or higher.

Support for generic addressing of .const space added in PTX ISA version 3.1.

Examples
    isspacep.const   iscnst, cptr;
    isspacep.global  isglbl, gptr;
    isspacep.local   islcl,  lptr;
    isspacep.shared  isshrd, sptr;

9.7.8.13. Data Movement and Conversion Instructions: cvta

cvta

Convert address from const, global, local, or shared state space to generic, or vice-versa. Take the generic address of a variable declared in const, global, local, or shared state space.

Syntax
// convert const, global, local, or shared address to generic address
cvta.space.size  p, a;        // source address in register a
cvta.space.size  p, var;      // get generic address of var
cvta.space.size  p, var+imm;  // generic address of var+offset

// convert generic address to const, global, local, or shared address
cvta.to.space.size  p, a;

.space = { .const, .global, .local, .shared };
.size  = { .u32, .u64 };
Description

Convert a const, global, local, or shared address to a generic address, or vice-versa. The source and destination addresses must be the same size. Use cvt.u32.u64 or cvt.u64.u32 to truncate or zero-extend addresses.

For variables declared in const, global, local, or shared state space, the generic address of the variable may be taken using cvta. The source is either a register or a variable defined in const, global, local, or shared memory with an optional offset.

When converting a generic address into a const, global, local, or shared address, the resulting address is undefined in cases where the generic address does not fall within the address window of the specified state space. A program may use isspacep to guard against such incorrect behavior.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

cvta.const and cvta.to.const introduced in PTX ISA version 3.1.

Note: The current implementation does not allow generic pointers to const space variables in programs that contain pointers to constant buffers passed as kernel parameters.

Target ISA Notes

cvta requires sm_20 or higher.

Examples
    cvta.const.u32   ptr,cvar;
    cvta.local.u32   ptr,lptr;
    cvta.shared.u32  p,As+4;
    cvta.to.global.u32  p,gptr;

9.7.8.14. Data Movement and Conversion Instructions: cvt

cvt

Convert a value from one type to another.

Syntax
cvt{.irnd}{.ftz}{.sat}.dtype.atype  d, a;  // integer rounding
cvt{.frnd}{.ftz}{.sat}.dtype.atype  d, a;  // fp rounding

.irnd  = { .rni, .rzi, .rmi, .rpi };
.frnd  = { .rn,  .rz,  .rm,  .rp  };
.dtype = .atype = { .u8, .u16, .u32, .u64,
                    .s8, .s16, .s32, .s64,
                         .f16, .f32, .f64 };
Description

Convert between different types and sizes.

Semantics 
d = convert(a);
Integer Notes

Integer rounding is required for float-to-integer conversions, and for same-size float-to-float conversions where the value is rounded to an integer. Integer rounding is illegal in all other instances.

Integer rounding modifiers:
.rni
round to nearest integer, choosing even integer if source is equidistant between two integers
.rzi
round to nearest integer in the direction of zero
.rmi
round to nearest integer in direction of negative infinity
.rpi
round to nearest integer in direction of positive infinity
Subnormal numbers:
sm_20+

By default, subnormal numbers are supported.

For cvt.ftz.dtype.f32 float-to-integer conversions and cvt.ftz.f32.f32 float-to-float conversions with integer rounding, subnormal inputs are flushed to sign-preserving zero.

sm_1x

For cvt.ftz.dtype.f32 float-to-integer conversions and cvt.ftz.f32.f32 float-to-float conversions with integer rounding, subnormal inputs are flushed to sign-preserving zero. The optional .ftz modifier may be specified in these cases for clarity.

Note: In PTX ISA versions 1.4 and earlier, the cvt instruction did not flush single-precision subnormal inputs or results to zero if the destination type size was 64-bits. The compiler will preserve this behavior for legacy PTX code.

Saturation modifier:
.sat

For integer destination types, .sat limits the result to MININT..MAXINT for the size of the operation. Note that saturation applies to both signed and unsigned integer types.

The saturation modifier is allowed only in cases where the destination type's value range is not a superset of the source type's value range; i.e., the .sat modifier is illegal in cases where saturation is not possible based on the source and destination types.

For float-to-integer conversions, the result is clamped to the destination range by default; i.e, .sat is redundant.

Floating Point Notes

Floating-point rounding is required for float-to-float conversions that result in loss of precision, and for integer-to-float conversions. Floating-point rounding is illegal in all other instances.

Floating-point rounding modifiers:
.rn
mantissa LSB rounds to nearest even
.rz
mantissa LSB rounds towards zero
.rm
mantissa LSB rounds towards negative infinity
.rp
mantissa LSB rounds towards positive infinity

A floating-point value may be rounded to an integral value using the integer rounding modifiers (see Integer Notes). The operands must be of the same size. The result is an integral value, stored in floating-point format.

Subnormal numbers:
sm_20+
By default, subnormal numbers are supported. Modifier .ftz may be specified to flush single-precision subnormal inputs and results to sign-preserving zero.
sm_1x
Single-precision subnormal inputs and results are flushed to sign-preserving zero. The optional .ftz modifier may be specified in these cases for clarity.

Note: In PTX ISA versions 1.4 and earlier, the cvt instruction did not flush single-precision subnormal inputs or results to zero if either source or destination type was .f64. The compiler will preserve this behavior for legacy PTX code. Specifically, if the PTX ISA version is 1.4 or earlier, single-precision subnormal inputs and results are flushed to sign-preserving zero only for cvt.f32.f16, cvt.f16.f32, and cvt.f32.f32 instructions.

Saturation modifier:
.sat:
For floating-point destination types, .sat limits the result to the range [0.0, 1.0]. NaN results are flushed to positive zero. Applies to .f16, .f32, and .f64 types.
Notes

A source register wider than the specified type may be used. The lower n bits corresponding to the instruction-type width are used in the conversion. See Operand Size Exceeding Instruction-Type Size for a description of these relaxed type-checking rules.

A destination register wider than the specified type may be used. The result of conversion is sign-extended to the destination register width for signed integers, and is zero-extended to the destination register width for unsigned, bit-size, and floating-point types. See Operand Size Exceeding Instruction-Type Size for a description of these relaxed type-checking rules.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

cvt to or from .f64 requires sm_13 or higher.

Examples
    cvt.f32.s32 f,i;
    cvt.s32.f64 j,r;     // float-to-int saturates by default
    cvt.rni.f32.f32 x,y; // round to nearest int, result is fp
    cvt.f32.f32 x,y;     // note .ftz behavior for sm_1x targets

Texture Instructions

This section describes PTX instructions for accessing textures and samplers. PTX supports the following operations on texture and sampler descriptors:
  • Static initialization of texture and sampler descriptors.
  • Module-scope and per-entry scope definitions of texture and sampler descriptors.
  • Ability to query fields within texture and sampler descriptors.

9.7.9.1. Texturing Modes

For working with textures and samplers, PTX has two modes of operation. In the unified mode, texture and sampler information is accessed through a single .texref handle. In the independent mode, texture and sampler information each have their own handle, allowing them to be defined separately and combined at the site of usage in the program. The advantage of unified mode is that it allows 128 samplers per kernel, with the restriction that they correspond 1-to-1 with the 128 possible textures per kernel. The advantage of independent mode is that textures and samplers can be mixed and matched, but the number of samplers is greatly restricted to 16 per kernel.

The texturing mode is selected using .target options texmode_unified and texmode_independent. A PTX module may declare only one texturing mode. If no texturing mode is declared, the module is assumed to use unified mode.

Example: calculate an element's power contribution as element's power/total number of elements. 

.target texmode_independent
.global .samplerref tsamp1 = { addr_mode_0 = clamp_to_border, 
                               filter_mode = nearest
                             };
...
.entry compute_power
  ( .param .texref tex1 )
{
  txq.width.b32  r6, [tex1]; // get tex1's width
  txq.height.b32 r5, [tex1]; // get tex1's height
  tex.2d.v4.f32.f32  {r1,r2,r3,r4}, [tex1, tsamp1, {f1,f2}];
  mul.u32 r5, r5, r6;
  add.f32 r1, r1, r2;
  add.f32 r3, r3, r4;
  add.f32 r1, r1, r3;
  cvt.f32.u32 r5, r5;
  div.f32 r1, r1, r5;
}

9.7.9.2. Mipmaps

A mipmap is a sequence of textures, each of which is a progressively lower resolution representation of the same image. The height and width of each image, or level of detail (LOD), in the mipmap is a power of two smaller than the previous level. Mipmaps are used in graphics applications to improve rendering speed and reduce aliasing artifacts. For example, a high-resolution mipmap image is used for objects that are close to the user; lower-resolution images are used as the object appears farther away. Mipmap filtering modes are provided when switching between two levels of detail (LODs) in order to avoid abrupt changes in visual fidelity.

Example: If the texture has a basic size of 256 by 256 pixels, then the associated mipmap set may contain a series of eight images, each one-fourth the total area of the previous one: 128×128 pixels, 64×64, 32×32, 16×16, 8×8, 4×4, 2×2, 1×1 (a single pixel). If, for example, a scene is rendering this texture in a space of 40×40 pixels, then either a scaled up version of the 32×32 (without trilinear interpolation) or an interpolation of the 64×64 and the 32×32 mipmaps (with trilinear interpolation) would be used.

The total number of LODs in a complete mipmap pyramid is calculated through the following equation:

numLODs = 1 + floor(log2(max(w, h, d)))

The finest LOD is called the base level and is the 0th level. The next (coarser) level is the 1st level, and so on. The coarsest level is the level of size (1 x 1 x 1). Each successively smaller mipmap level has half the {width, height, depth} of the previous level, but if this half value is a fractional value, it's rounded down to the next largest integer. Essentially, the size of a mipmap level can be specified as:
  • max(1, floor(w_b / 2^i)) x
  • max(1, floor(h_b / 2^i)) x
  • max(1, floor(d_b / 2^i))

where i is the ith level beyond the 0th level (the base level). And w_b, h_b and d_b are the width, height and depth of the base level respectively.

PTX support for mipmaps

The PTX tex instruction supports three modes for specifying the LOD: base, level, and gradient. In base mode, the instruction always picks level 0. In level mode, an additional argument is provided to specify the LOD to fetch from. In gradmode, two floating-point vector arguments provide partials (e.g., {ds/dx, dt/dx} and {ds/dy, dt/dy} for a 2d texture), which the tex instruction uses to compute the LOD.

These instructions provide access to texture memory.
  • tex
  • tld4
  • txq

9.7.9.3. Texture Instructions: tex

tex

Perform a texture memory lookup.

Syntax
tex.geom.v4.dtype.ctype  d, [a, c] {, e} {, f};
tex.geom.v4.dtype.ctype  d, [a, b, c] {, e} {, f};  // explicit sampler 

tex.geom.v2.f16x2.ctype  d, [a, c] {, e} {, f};
tex.geom.v2.f16x2.ctype  d, [a, b, c] {, e} {, f};  // explicit sampler

// mipmaps
tex.base.geom.v4.dtype.ctype   d, [a, {b,} c] {, e} {, f};
tex.level.geom.v4.dtype.ctype  d, [a, {b,} c], lod {, e} {, f};
tex.grad.geom.v4.dtype.ctype   d, [a, {b,} c], dPdx, dPdy {, e} {, f};

tex.base.geom.v2.f16x2.ctype   d, [a, {b,} c] {, e} {, f};
tex.level.geom.v2.f16x2.ctype  d, [a, {b,} c], lod {, e} {, f};
tex.grad.geom.v2.f16x2.ctype   d, [a, {b,} c], dPdx, dPdy {, e} {, f};

.geom  = { .1d, .2d, .3d, .a1d, .a2d, .cube, .acube, .2dms, .a2dms };
.dtype = { .u32, .s32, .f16,  .f32 };
.ctype = {       .s32, .f32 };          // .cube, .acube require .f32
                                        // .2dms, .a2dms require .s32
Description

tex.{1d,2d,3d}

Texture lookup using a texture coordinate vector. The instruction loads data from the texture named by operand a at coordinates given by operand c into destination d. Operand c is a scalar or singleton tuple for 1d textures; is a two-element vector for 2d textures; and is a four-element vector for 3d textures, where the fourth element is ignored. An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

An optional operand e may be specified. Operand e is a vector of .s32 values that specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset value is in the range of -8 to +7. Operand e is a singleton tuple for 1d textures; is a two element vector 2d textures; and is four-element vector for 3d textures, where the fourth element is ignored.

An optional operand f may be specified for depth textures. Depth textures are special type of textures which hold data from the depth buffer. Depth buffer contains depth information of each pixel. Operand f is .f32 scalar value that specifies depth compare value for depth textures. Each element fetched from texture is compared against value given in f operand. If comparison passes, result is 1.0; otherwise result is 0.0. These per element comparison results are used to the filtering. When using depth compare operand, the elements in texture coordinate vector c have .f32 type.

Depth compare operand is not supported for 3d textures.

The instruction returns a two-element vector for destination type f16x2. For all other destination types, the instruction returns a four-element vector. Coordinates may be given in either signed 32-bit integer or 32-bit floating point form.

A texture base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.

tex.{a1d,a2d}

Texture array selection, followed by texture lookup. The instruction first selects a texture from the texture array named by operand a using the index given by the first element of the array coordinate vector c. The instruction then loads data from the selected texture at coordinates given by the remaining elements of operand c into destination d. Operand c is a bit-size type vector or tuple containing an index into the array of textures followed by coordinates within the selected texture, as follows:
  • For 1d texture arrays, operand c has type .v2.b32. The first element is interpreted as an unsigned integer index (.u32) into the texture array, and the second element is interpreted as a 1d texture coordinate of type .ctype.
  • For 2d texture arrays, operand c has type .v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the texture array, and the next two elements are interpreted as 2d texture coordinates of type .ctype. The fourth element is ignored.

An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

An optional operand e may be specified. Operand e is a vector of .s32 values that specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset value is in the range of -8 to +7. Operand e is a singleton tuple for 1d texture arrays; and is a two element vector 2d texture arrays.

An optional operand f may be specified for depth textures arrays. Operand f is .f32 scalar value that specifies depth compare value for depth textures. When using depth compare operand, the coordinates in texture coordinate vector c have .f32 type.

The instruction returns a two-element vector for destination type f16x2. For all other destination types, the instruction returns a four-element vector. The texture array index is a 32-bit unsigned integer, and texture coordinate elements are 32-bit signed integer or floating point values.

tex.cube

Cubemap texture lookup. The instruction loads data from the cubemap texture named by operand a at coordinates given by operand c into destination d. Cubemap textures are special two-dimensional layered textures consisting of six layers that represent the faces of a cube. All layers in a cubemap are of the same size and are square (i.e., width equals height).

When accessing a cubemap, the texture coordinate vector c has type .v4.f32, and comprises three floating-point coordinates (s, t, r) and a fourth padding argument which is ignored. Coordinates (s, t, r) are projected onto one of the six cube faces. The (s, t, r) coordinates can be thought of as a direction vector emanating from the center of the cube. Of the three coordinates (s, t, r), the coordinate of the largest magnitude (the major axis) selects the cube face. Then, the other two coordinates (the minor axes) are divided by the absolute value of the major axis to produce a new (s, t) coordinate pair to lookup into the selected cube face.

An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

Offset vector operand e is not supported for cubemap textures.

an optional operand f may be specified for cubemap depth textures. operand f is .f32 scalar value that specifies depth compare value for cubemap depth textures.

tex.acube

Cubemap array selection, followed by cubemap lookup. The instruction first selects a cubemap texture from the cubemap array named by operand a using the index given by the first element of the array coordinate vector c. The instruction then loads data from the selected cubemap texture at coordinates given by the remaining elements of operand c into destination d.

Cubemap array textures consist of an array of cubemaps, i.e., the total number of layers is a multiple of six. When accessing a cubemap array texture, the coordinate vector c has type .v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the cubemap array, and the remaining three elements are interpreted as floating-point cubemap coordinates (s, t, r), used to lookup in the selected cubemap as described above.

An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

Offset vector operand e is not supported for cubemap texture arrays.

An optional operand f may be specified for cubemap depth texture arrays. Operand f is .f32 scalar value that specifies depth compare value for cubemap depth textures.

tex.2dms

Multi-sample texture lookup using a texture coordinate vector. Multi-sample textures consist of multiple samples per data element. The instruction loads data from the texture named by operand a from sample number given by first element of the operand c, at coordinates given by remaining elements of operand c into destination d. When accessing a multi-sample texture, texture coordinate vector c has type .v4.b32. The first element in operand c is interpreted as unsigned integer sample number (.u32), and the next two elements are interpreted as signed integer (.s32) 2d texture coordinates. The fourth element is ignored. An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

An optional operand e may be specified. Operand e is a vector of type .v2.s32 that specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset value is in the range of -8 to +7.

Depth compare operand f is not supported for multi-sample textures.

tex.a2dms

Multi-sample texture array selection, followed by multi-sample texture lookup. The instruction first selects a multi-sample texture from the multi-sample texture array named by operand a using the index given by the first element of the array coordinate vector c. The instruction then loads data from the selected multi-sample texture from sample number given by second element of the operand c, at coordinates given by remaining elements of operand c into destination d. When accessing a multi-sample texture array, texture coordinate vector c has type .v4.b32. The first element in operand c is interpreted as unsigned integer sampler number, the second element is interpreted as unsigned integer index (.u32) into the multi-sample texture array and the next two elements are interpreted as signed integer (.s32) 2d texture coordinates. An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

An optional operand e may be specified. Operand e is a vector of type .v2.s32 values that specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset value is in the range of -8 to +7.

Depth compare operand f is not supported for multi-sample texture arrays.

Mipmaps

.base (lod zero)
Pick level 0 (base level). This is the default if no mipmap mode is specified. No additional arguments.
.level (lod explicit)
Requires an additional 32-bit scalar argument, lod, which contains the LOD to fetch from. The type of lod follows .ctype (either .s32 or .f32). Geometries .2dms and .a2dms are not supported in this mode.
.grad (lod gradient)
Requires two .f32 vectors, dPdx and dPdy, that specify the partials. The vectors are singletons for 1d and a1d textures; are two-element vectors for 2d and a2d textures; and are four-element vectors for 3d, cube and acube textures, where the fourth element is ignored for 3d and cube geometries. Geometries .2dms and .a2dms are not supported in this mode.

For mipmap texture lookup, an optional operand e may be specified. Operand e is a vector of .s32 that specifies coordinate offset. Offset is applied to coordinates before doing texture lookup. Offset value is in the range of -8 to +7. Offset vector operand is not supported for cube and cubemap geometries.

An optional operand f may be specified for mipmap textures. Operand f is .f32 scalar value that specifies depth compare value for depth textures. When using depth compare operand, the coordinates in texture coordinate vector c have .f32 type.

Depth compare operand is not supported for 3d textures.

Indirect texture access

Beginning with PTX ISA version 3.1, indirect texture access is supported in unified mode for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .texref variable.

Notes

For compatibility with prior versions of PTX, the square brackets are not required and .v4 coordinate vectors are allowed for any geometry, with the extra elements being ignored.

PTX ISA Notes

Unified mode texturing introduced in PTX ISA version 1.0. Extension using opaque .texref and .samplerref types and independent mode texturing introduced in PTX ISA version 1.5.

Texture arrays tex.{a1d,a2d} introduced in PTX ISA version 2.3.

Cubemaps and cubemap arrays introduced in PTX ISA version 3.0.

Support for mipmaps introduced in PTX ISA version 3.1.

Indirect texture access introduced in PTX ISA version 3.1.

Multi-sample textures and multi-sample texture arrays introduced in PTX ISA version 3.2.

Support for textures returning f16 and f16x2 data introduced in PTX ISA version 4.2.

Support for tex.grad.{cube, acube} introduced in PTX ISA version 4.3.

Offset vector operand introduced in PTX ISA version 4.3.

Depth compare operand introduced in PTX ISA version 4.3.

Target ISA Notes

Supported on all target architectures.

The cubemap array geometry (.acube) requires sm_20 or higher.

Mipmaps require sm_20 or higher.

Indirect texture access requires sm_20 or higher.

Multi-sample textures and multi-sample texture arrays require sm_30 or higher.

Texture fetch returning f16 and f16x2 data require sm_53 or higher.

tex.grad.{cube, acube} requires sm_20 or higher.

Offset vector operand requires sm_30 or higher.

Depth compare operand requires sm_30 or higher.

Examples
    // Example of unified mode texturing
    // - f4 is required to pad four-element tuple and is ignored
    tex.3d.v4.s32.s32  {r1,r2,r3,r4}, [tex_a,{f1,f2,f3,f4}];

    // Example of independent mode texturing
    tex.1d.v4.s32.f32  {r1,r2,r3,r4}, [tex_a,smpl_x,{f1}];

    // Example of 1D texture array, independent texturing mode
    tex.a1d.v4.s32.s32 {r1,r2,r3,r4}, [tex_a,smpl_x,{idx,s1}];           

    // Example of 2D texture array, unified texturing mode
    // - f3 is required to pad four-element tuple and is ignored 
    tex.a2d.v4.s32.f32 {r1,r2,r3,r4}, [tex_a,{idx,f1,f2,f3}];

    // Example of cubemap array, unified textureing mode
    tex.acube.v4.f32.f32 {r0,r1,r2,r3}, [tex_cuarray,{idx,f1,f2,f3}];

    // Example of multi-sample texture, unified texturing mode
    tex.2dms.v4.s32.s32 {r0,r1,r2,r3}, [tex_ms,{sample,r6,r7,r8}];

    // Example of multi-sample texture, independent texturing mode
    tex.2dms.v4.s32.s32 {r0,r1,r2,r3}, [tex_ms, smpl_x,{sample,r6,r7,r8}];

    // Example of multi-sample texture array, unified texturing mode
    tex.a2dms.v4.s32.s32 {r0,r1,r2,r3}, [tex_ams,{idx,sample,r6,r7}];

    // Example of texture returning .f16 data
    tex.1d.v4.f16.f32  {h1,h2,h3,h4}, [tex_a,smpl_x,{f1}];

    // Example of texture returning .f16x2 data
    tex.1d.v2.f16x2.f32  {h1,h2}, [tex_a,smpl_x,{f1}];

    // Example of 3d texture array access with tex.grad,unified texturing mode
    tex.grad.3d.v4.f32.f32 {%f4,%f5,%f6,%f7},[tex_3d,{%f0,%f0,%f0,%f0}],     
                    {fl0,fl1,fl2,fl3},{fl0,fl1,fl2,fl3};

   // Example of cube texture array access with tex.grad,unified texturing mode
    tex.grad.cube.v4.f32.f32{%f4,%f5,%f6,%f7},[tex_cube,{%f0,%f0,%f0,%f0}],     
                    {fl0,fl1,fl2,fl3},{fl0,fl1,fl2,fl3};

    // Example of 1d texture lookup with offset, unified texturing mode
    tex.1d.v4.s32.f32  {r1,r2,r3,r4}, [tex_a, {f1}], {r5};

    // Example of 2d texture array lookup with offset, unified texturing mode
    tex.a2d.v4.s32.f32  {r1,r2,r3,r4}, [tex_a,{idx,f1,f2}], {f5,f6};

    // Example of 2d mipmap texture lookup with offset, unified texturing mode
    tex.level.2d.v4.s32.f32  {r1,r2,r3,r4}, [tex_a,{f1,f2}],    
                             flvl, {r7, r8};

    // Example of 2d depth texture lookup with compare, unified texturing mode
    tex.1d.v4.f32.f32  {f1,f2,f3,f4}, [tex_a, {f1}], f0;
    
    // Example of depth 2d texture array lookup with offset, compare      
    tex.a2d.v4.s32.f32  {f0,f1,f2,f3}, [tex_a,{idx,f4,f5}], {r5,r6}, f6;

9.7.9.4. Texture Instructions: tld4

tld4

Perform a texture fetch of the 4-texel bilerp footprint.

Syntax
tld4.comp.2d.v4.dtype.f32    d, [a, c] {, e} {, f};
tld4.comp.geom.v4.dtype.f32  d, [a, b, c] {, e} {, f};  // explicit sampler

.comp  = { .r, .g, .b, .a };
.geom  = { .2d, .a2d, .cube, .acube };
.dtype = { .u32, .s32, .f32 };
Description

Texture fetch of the 4-texel bilerp footprint using a texture coordinate vector. The instruction loads the bilerp footprint from the texture named by operand a at coordinates given by operand c into vector destination d. The texture component fetched for each texel sample is specified by .comp. The four texel samples are placed into destination vector d in counter-clockwise order starting at lower left.

An optional texture sampler b may be specified. If no sampler is specified, the sampler behavior is a property of the named texture.

An optional operand f may be specified for depth textures. Depth textures are special type of textures which hold data from the depth buffer. Depth buffer contains depth information of each pixel. Operand f is .f32 scalar value that specifies depth compare value for depth textures. Each element fetched from texture is compared against value given in f operand. If comparison passes, result is 1.0; otherwise result is 0.0. These per element comparison results are used to the filtering.

A texture base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.

tld4.2d

For 2D textures, operand c specifies coordinates as a two-element, 32-bit floating-point vector.

An optional operand e may be specified. Operand e is a vector of type .v2.s32 that specifies coordinate offset. Offset is applied to coordinates before doing texture fetch. Offset value is in the range of -8 to +7.

tld4.a2d

Texture array selection, followed by tld4 texture fetch of 2d texture. For 2d texture arrays operand c is a four element, 32-bit vector. The first element in operand c is interpreted as an unsigned integer index (.u32) into the texture array, and the next two elements are interpreted as 32-bit floating point coordinates of 2d texture. The fourth element is ignored.

An optional operand e may be specified. Operand e is a vector of type .v2.s32 that specifies coordinate offset. Offset is applied to coordinates before doing texture fetch. Offset value is in the range of -8 to +7.

tld4.cube

For cubemap textures, operand c specifies four-element vector which comprises three floating-point coordinates (s, t, r) and a fourth padding argument which is ignored.

Cubemap textures are special two-dimensional layered textures consisting of six layers that represent the faces of a cube. All layers in a cubemap are of the same size and are square (i.e., width equals height).

Coordinates (s, t, r) are projected onto one of the six cube faces. The (s, t, r) coordinates can be thought of as a direction vector emanating from the center of the cube. Of the three coordinates (s, t, r), the coordinate of the largest magnitude (the major axis) selects the cube face. Then, the other two coordinates (the minor axes) are divided by the absolute value of the major axis to produce a new (s, t) coordinate pair to lookup into the selected cube face.

Offset vector operand e is not supported for cubemap textures.

tld4.acube

Cubemap array selection, followed by tld4 texture fetch of cubemap texture. The first element in operand c is interpreted as an unsigned integer index (.u32) into the cubemap texture array, and the remaining three elements are interpreted as floating-point cubemap coordinates (s, t, r), used to lookup in the selected cubemap.

Offset vector operand e is not supported for cubemap texture arrays.

Indirect texture access

Beginning with PTX ISA version 3.1, indirect texture access is supported in unified mode for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .texref variable.

PTX ISA Notes

Introduced in PTX ISA version 2.2.

Indirect texture access introduced in PTX ISA version 3.1.

tld4.{a2d,cube,acube} introduced in PTX ISA version 4.3.

Offset vector operand introduced in PTX ISA version 4.3.

Depth compare operand introduced in PTX ISA version 4.3.

Target ISA Notes

tld4 requires sm_20 or higher.

Indirect texture access requires sm_20 or higher.

tld4.{a2d,cube,acube} requires sm_30 or higher.

Offset vector operand requires sm_30 or higher.

Depth compare operand requires sm_30 or higher.

Examples
    //Example of unified mode texturing
    tld4.r.2d.v4.s32.f32  {r1,r2,r3,r4}, [tex_a,{f1,f2}];

    // Example of independent mode texturing
    tld4.r.2d.v4.u32.f32  {u1,u2,u3,u4}, [tex_a,smpl_x,{f1,f2}];

    // Example of unified mode texturing using offset
    tld4.r.2d.v4.s32.f32  {r1,r2,r3,r4}, [tex_a,{f1,f2}], {r5, r6};

   // Example of unified mode texturing using compare
    tld4.r.2d.v4.f32.f32  {f1,f2,f3,f4}, [tex_a,{f5,f6}], f7;

9.7.9.5. Texture Instructions: txq

txq

Query texture and sampler attributes.

Syntax
txq.tquery.b32         d, [a];       // texture attributes
txq.level.tlquery.b32  d, [a], lod;  // texture attributes
txq.squery.b32         d, [a];       // sampler attributes

.tquery  = { .width, .height, .depth,
             .channel_data_type, .channel_order,
             .normalized_coords, .array_size,
             .num_mipmap_levels, .num_samples};

.tlquery = { .width, .height, .depth };

.squery  = { .force_unnormalized_coords, .filter_mode,
             .addr_mode_0, addr_mode_1, addr_mode_2 };
Description

Query an attribute of a texture or sampler. Operand a is either a .texref or .samplerref variable, or a .u64 register.

Query Returns

.width

.height

.depth

 value in elements
.channel_data_type Unsigned integer corresponding to source language's channel data type enumeration. If the source language combines channel data type and channel order into a single enumeration type, that value is returned for both channel_data_type and channel_order queries.
.channel_order Unsigned integer corresponding to source language's channel order enumeration. If the source language combines channel data type and channel order into a single enumeration type, that value is returned for both channel_data_type and channel_order queries.
.normalized_coords 1 (True) or 0 (False).
.force_unnormalized_coords 1 (True) or 0 (False). Defined only for .samplerref variables in independent texture mode. Overrides the normalized_coords field of a .texref variable used with a .samplerref in a tex instruction.
.filter_mode Integer from enum { nearest, linear }

.addr_mode_0

.addr_mode_1

.addr_mode_2

 Integer from enum { wrap, mirror, clamp_ogl, clamp_to_edge, clamp_to_border }

.array_size

 For a texture array, number of textures in array, 0 otherwise.

.num_mipmap_levels

 For a mipmapped texture, number of levels of details (LOD), 0 otherwise.

.num_samples

 For a multi-sample texture, number of samples, 0 otherwise.

Texture attributes are queried by supplying a .texref argument to txq. In unified mode, sampler attributes are also accessed via a .texref argument, and in independent mode sampler attributes are accessed via a separate .samplerref argument.

txq.level

txq.level requires an additional 32bit integer argument, lod, which specifies LOD and queries requested attribute for the specified LOD.

Indirect texture access

Beginning with PTX ISA version 3.1, indirect texture access is supported in unified mode for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .texref variable.

PTX ISA Notes

Introduced in PTX ISA version 1.5.

Channel data type and channel order queries were added in PTX ISA version 2.1.

The .force_unnormalized_coords query was added in PTX ISA version 2.2.

Indirect texture access introduced in PTX ISA version 3.1.

.array_size, .num_mipmap_levels, .num_samples samples queries were added in PTX ISA version 4.1.

txq.level introduced in PTX ISA version 4.3.

Target ISA Notes

Supported on all target architectures.

Indirect texture access requires sm_20 or higher.

Querying the number of mipmap levels requires sm_20 or higher.

Querying the number of samples requires sm_30 or higher.

txq.level requires sm_30 or higher.

Examples
    txq.width.b32       %r1, [tex_A];
    txq.filter_mode.b32 %r1, [tex_A];   // unified mode
    txq.addr_mode_0.b32 %r1, [smpl_B];  // independent mode
    txq.level.width.b32 %r1, [tex_A], %r_lod;

9.7.9.6. Texture Instructions: istypep

istypep

Query whether a register points to an opaque variable of a specified type.

Syntax
istypep.type   p, a;  // result is .pred

.type = { .texref, .samplerref, .surfref };
Description

Write predicate register p with 1 if register a points to an opaque variable of the specified type, and with 0 otherwise. Destination p has type .pred; the source address operand must be of type .u64.

PTX ISA Notes

Introduced in PTX ISA version 4.0.

Target ISA Notes

istypep requires sm_30 or higher.

Examples
    istypep.texref istex, tptr;
    istypep.samplerref issampler, sptr;
    istypep.surfref issurface, surfptr;

9.7.10. Surface Instructions

This section describes PTX instructions for accessing surfaces. PTX supports the following operations on surface descriptors:
  • Static initialization of surface descriptors.
  • Module-scope and per-entry scope definitions of surface descriptors.
  • Ability to query fields within surface descriptors.
These instructions provide access to surface memory.
  • suld
  • sust
  • sured
  • suq

9.7.10.1. Surface Instructions: suld

suld

Load from surface memory.

Syntax
suld.b.geom{.cop}.vec.dtype.clamp  d, [a, b];  // unformatted

.geom  = { .1d, .2d, .3d, .a1d, .a2d };
.cop   = { .ca, .cg, .cs, .cv };               // cache operation
.vec   = { none, .v2, .v4 };
.dtype = { .b8 , .b16, .b32, .b64 };
.clamp = { .trap, .clamp, .zero };
Description

suld.b.{1d,2d,3d}

Load from surface memory using a surface coordinate vector. The instruction loads data from the surface named by operand a at coordinates given by operand b into destination d. Operand a is a .surfref variable or .u64 register. Operand b is a scalar or singleton tuple for 1d surfaces; is a two-element vector for 2d surfaces; and is a four-element vector for 3d surfaces, where the fourth element is ignored. Coordinate elements are of type .s32.

suld.b performs an unformatted load of binary data. The lowest dimension coordinate represents a byte offset into the surface and is not scaled, and the size of the data transfer matches the size of destination operand d.

suld.b.{a1d,a2d}

Surface layer selection, followed by a load from the selected surface. The instruction first selects a surface layer from the surface array named by operand a using the index given by the first element of the array coordinate vector b. The instruction then loads data from the selected surface at coordinates given by the remaining elements of operand b into destination d. Operand a is a .surfref variable or .u64 register. Operand b is a bit-size type vector or tuple containing an index into the array of surfaces followed by coordinates within the selected surface, as follows:

For 1d surface arrays, operand b has type .v2.b32. The first element is interpreted as an unsigned integer index (.u32) into the surface array, and the second element is interpreted as a 1d surface coordinate of type .s32.

For 2d surface arrays, operand b has type .v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the surface array, and the next two elements are interpreted as 2d surface coordinates of type .s32. The fourth element is ignored.

A surface base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.

The .clamp field specifies how to handle out-of-bounds addresses:
.trap
causes an execution trap on out-of-bounds addresses
.clamp
loads data at the nearest surface location (sized appropriately)
.zero
loads zero for out-of-bounds addresses

Indirect surface access

Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .surfref variable.

PTX ISA Notes

suld.b.trap introduced in PTX ISA version 1.5.

Additional clamp modifiers and cache operations introduced in PTX ISA version 2.0.

suld.b.3d and suld.b.{a1d,a2d} introduced in PTX ISA version 3.0.

Indirect surface access introduced in PTX ISA version 3.1.

Target ISA Notes

suld.b supported on all target architectures.

sm_1x targets support only the .trap clamping modifier.

suld.3d and suld.{a1d,a2d} require sm_20 or higher.

Indirect surface access requires sm_20 or higher.

Cache operations require sm_20 or higher.

Examples
    suld.b.1d.v4.b32.trap  {s1,s2,s3,s4}, [surf_B, {x}];
    suld.b.3d.v2.b64.trap  {r1,r2}, [surf_A, {x,y,z,w}];
    suld.b.a1d.v2.b32      {r0,r1}, [surf_C, {idx,x}];
    suld.b.a2d.b32         r0, [surf_D, {idx,x,y,z}];  // z ignored

9.7.10.2. Surface Instructions: sust

sust

Store to surface memory.

Syntax
sust.b.{1d,2d,3d}{.cop}.vec.ctype.clamp  [a, b], c;  // unformatted
sust.p.{1d,2d,3d}.vec.b32.clamp          [a, b], c;  // formatted

sust.b.{a1d,a2d}{.cop}.vec.ctype.clamp   [a, b], c;  // unformatted

.cop   = { .wb, .cg, .cs, .wt };                     // cache operation
.vec   = { none, .v2, .v4 };
.ctype = { .b8 , .b16, .b32, .b64 };
.clamp = { .trap, .clamp, .zero };
Description

sust.{1d,2d,3d}

Store to surface memory using a surface coordinate vector. The instruction stores data from operand c to the surface named by operand a at coordinates given by operand b. Operand a is a .surfref variable or .u64 register. Operand b is a scalar or singleton tuple for 1d surfaces; is a two-element vector for 2d surfaces; and is a four-element vector for 3d surfaces, where the fourth element is ignored. Coordinate elements are of type .s32.

sust.b performs an unformatted store of binary data. The lowest dimension coordinate represents a byte offset into the surface and is not scaled. The size of the data transfer matches the size of source operand c.

sust.p performs a formatted store of a vector of 32-bit data values to a surface sample. The source vector elements are interpreted left-to-right as R, G, B, and A surface components. These elements are written to the corresponding surface sample components. Source elements that do not occur in the surface sample are ignored. Surface sample components that do not occur in the source vector will be written with an unpredictable value. The lowest dimension coordinate represents a sample offset rather than a byte offset.

The source data interpretation is based on the surface sample format as follows: If the surface format contains UNORM, SNORM, or FLOAT data, then .f32 is assumed; if the surface format contains UINT data, then .u32 is assumed; if the surface format contains SINT data, then .s32 is assumed. The source data is then converted from this type to the surface sample format.

sust.b.{a1d,a2d}

Surface layer selection, followed by an unformatted store to the selected surface. The instruction first selects a surface layer from the surface array named by operand a using the index given by the first element of the array coordinate vector b. The instruction then stores the data in operand c to the selected surface at coordinates given by the remaining elements of operand b. Operand a is a .surfref variable or .u64 register. Operand b is a bit-size type vector or tuple containing an index into the array of surfaces followed by coordinates within the selected surface, as follows:
  • For 1d surface arrays, operand b has type .v2.b32. The first element is interpreted as an unsigned integer index (.u32) into the surface array, and the second element is interpreted as a 1d surface coordinate of type .s32.
  • For 2d surface arrays, operand b has type .v4.b32. The first element is interpreted as an unsigned integer index (.u32) into the surface array, and the next two elements are interpreted as 2d surface coordinates of type .s32. The fourth element is ignored.

A surface base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.

The .clamp field specifies how to handle out-of-bounds addresses:
.trap
causes an execution trap on out-of-bounds addresses
.clamp
stores data at the nearest surface location (sized appropriately)
.zero
drops stores to out-of-bounds addresses

Indirect surface access

Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .surfref variable.

PTX ISA Notes

sust.b.trap introduced in PTX ISA version 1.5.  sust.p, additional clamp modifiers, and cache operations introduced in PTX ISA version 2.0.

sust.b.3d and sust.b.{a1d,a2d} introduced in PTX ISA version 3.0.

Indirect surface access introduced in PTX ISA version 3.1.

Target ISA Notes

sust.b supported on all target architectures.

sm_1x targets support only the .trap clamping modifier.

sust.3d and sust.{a1d,a2d} require sm_20 or higher.

sust.p requires sm_20 or higher.

Indirect surface access requires sm_20 or higher.

Cache operations require sm_20 or higher.

Examples
    sust.p.1d.v4.b32.trap  [surf_B, {x}], {f1,f2,f3,f4};
    sust.b.3d.v2.b64.trap  [surf_A, {x,y,z,w}], {r1,r2};
    sust.b.a1d.v2.b64      [surf_C, {idx,x}], {r1,r2};
    sust.b.a2d.b32         [surf_D, {idx,x,y,z}], r0;  // z ignored

9.7.10.3. Surface Instructions: sured

sured

Reduce surface memory.

Syntax
sured.b.op.geom.ctype.clamp  [a,b],c; // byte addressing
sured.p.op.geom.ctype.clamp  [a,b],c; // sample addressing

.op    = { .add, .min, .max, .and, .or };
.geom  = { .1d, .2d, .3d };
.ctype = { .u32, .u64, .s32, .b32 };  // for sured.b
.ctype = { .b32 };                    // for sured.p
.clamp = { .trap, .clamp, .zero };
Description

Reduction to surface memory using a surface coordinate vector. The instruction performs a reduction operation with data from operand c to the surface named by operand a at coordinates given by operand b. Operand a is a .surfref variable or .u64 register. Operand b is a scalar or singleton tuple for 1d surfaces; is a two-element vector for 2d surfaces; and is a four-element vector for 3d surfaces, where the fourth element is ignored. Coordinate elements are of type .s32.

sured.b performs an unformatted reduction on .u32, .s32, .b32, or .u64 data.  The lowest dimension coordinate represents a byte offset into the surface and is not scaled. Operation add applies to .u32, .u64, and .s32 types; min and max apply to .u32 and .s32 types; operations and and or apply to .b32 type.

sured.p performs a reduction on sample-addressed 32-bit data. The lowest dimension coordinate represents a sample offset rather than a byte offset.  The instruction type is restricted to .b32, and the data is interpreted as .s32 or .u32 based on the surface sample format as follows: if the surface format contains UINT data, then .u32 is assumed; if the surface format contains SINT data, then .s32 is assumed.

A surface base address is assumed to be aligned to a 16 byte boundary, and the address given by the coordinate vector must be naturally aligned to a multiple of the access size. If an address is not properly aligned, the resulting behavior is undefined; i.e., the access may proceed by silently masking off low-order address bits to achieve proper rounding, or the instruction may fault.

The .clamp field specifies how to handle out-of-bounds addresses:
.trap
causes an execution trap on out-of-bounds addresses
.clamp
stores data at the nearest surface location (sized appropriately)
.zero
drops stores to out-of-bounds addresses

Indirect surface access

Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .surfref variable.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Indirect surface access introduced in PTX ISA version 3.1.

Target ISA Notes

sured requires sm_20 or higher.

Indirect surface access requires sm_20 or higher.

Examples
    sured.b.add.2d.u32.trap  [surf_A, {x,y}], r1;
    sured.p.min.1d.b32.trap  [surf_B, {x}], r1;

Surface Instructions: suq

suq

Query a surface attribute.

Syntax
suq.query.b32   d, [a];

.query = { .width, .height, .depth, 
           .channel_data_type, .channel_order, 
           .array_size, .memory_layout };
Description

Query an attribute of a surface. Operand a is a .surfref variable or a .u64 register.

Query Returns

.width

.height

.depth

 value in elements
.channel_data_type Unsigned integer corresponding to source language's channel data type enumeration. If the source language combines channel data type and channel order into a single enumeration type, that value is returned for both channel_data_type and channel_order queries.
.channel_order Unsigned integer corresponding to source language's channel order enumeration. If the source language combines channel data type and channel order into a single enumeration type, that value is returned for both channel_data_type and channel_order queries.

.array_size

 For a surface array, number of surfaces in array, 0 otherwise.

.memory_layout

 1 for surface with linear memory layout; 0 otherwise

Indirect surface access

Beginning with PTX ISA version 3.1, indirect surface access is supported for target architecture sm_20 or higher. In indirect access, operand a is a .u64 register holding the address of a .surfref variable.

PTX ISA Notes

Introduced in PTX ISA version 1.5.

Channel data type and channel order queries added in PTX ISA version 2.1.

Indirect surface access introduced in PTX ISA version 3.1.

The .array_size query was added in PTX ISA version 4.1.

The .memory_layout query was added in PTX ISA version 4.2.

Target ISA Notes

Supported on all target architectures.

Indirect surface access requires sm_20 or higher.

Examples
    suq.width.b32       %r1, [surf_A];

9.7.11. Control Flow Instructions

The following PTX instructions and syntax are for controlling execution in a PTX program:
  • {}
  • @
  • bra
  • call
  • ret
  • exit

9.7.11.1. Control Flow Instructions: {}

{}

Instruction grouping.

Syntax
{ instructionList }
Description

The curly braces create a group of instructions, used primarily for defining a function body. The curly braces also provide a mechanism for determining the scope of a variable: any variable declared within a scope is not available outside the scope.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    { add.s32  a,b,c; mov.s32  d,a; }

9.7.11.2. Control Flow Instructions: @

@

Predicated execution.

Syntax
@{!}p    instruction;
Description

Execute an instruction or instruction block for threads that have the guard predicate True. Threads with a False guard predicate do nothing.

Semantics

If {!}p then instruction

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    setp.eq.f32  p,y,0;     // is y zero?
@!p div.f32      ratio,x,y  // avoid division by zero

@q  bra L23;                // conditional branch

9.7.11.3. Control Flow Instructions: bra

bra

Branch to a target and continue execution there.

Syntax
@p   bra{.uni}  tgt;           // tgt is a label
     bra{.uni}  tgt;           // unconditional branch
Description

Continue execution at the target. Conditional branches are specified by using a guard predicate. The branch target must be a label. The branch target is a label.

bra.uni is guaranteed to be non-divergent, meaning that all threads in a warp have identical values for the guard predicate and branch target.

Semantics
if (p) {
    pc = tgt;
}
PTX ISA Notes

Introduced in PTX ISA version 1.0.

Unimplemented indirect branch introduced in PTX ISA version 2.1 has been removed from the spec.

Target ISA Notes

Supported on all target architectures.

Examples
    bra.uni  L_exit;    // uniform unconditional jump
    @q  bra      L23;   // conditional branch

9.7.11.4. Control Flow Instructions: brx.idx

brx.idx

Branch to a label indexed from a list of potential branch targets.

Syntax
@p    brx.idx{.uni} index, tlist;
      brx.idx{.uni} index, tlist;
Description

Index into a list of possible destination labels, and continue execution from the chosen label. Conditional branches are specified by using a guard predicate.

When using brx.idx.uni, the PTX producer must guarantee that the branch is non-divergent, i.e. all threads in a warp have identical values for the guard predicate and the index argument.

The index is a .u32 register. The tlist must be the label of a .branchtargets directive. It is accessed as a zero-based sequence using the index. Behaviour is undefined if the value of the index is greater than or equal to the length of tlist.

The .branchtargets directive must be defined in the local function scope before it is used. It must refer to labels within the current function.

Semantics
if (p) {
    if (index < length(tlist)) {
      pc = tlist[index];
    } else {
      pc = undefined;
    }
}
PTX ISA Notes

Introduced in PTX ISA version 6.0.

Target ISA Notes

Requires sm_30 or higher.

Examples
  .function foo () {
      .reg .u32 %r0;
      ...
      L1:
      ...
      L2:
      ...
      L3:
      ...
      ts: .branchtargets L1, L2, L3;
      @p brx.idx %r0, ts;
      ...
  }

9.7.11.5. Control Flow Instructions: call

call

Call a function, recording the return location.

Syntax
// direct call to named function, func is a symbol
call{.uni} (ret-param), func, (param-list);
call{.uni} func, (param-list);
call{.uni} func;

// indirect call via pointer, with full list of call targets
call{.uni} (ret-param), fptr, (param-list), flist;
call{.uni} fptr, (param-list), flist;
call{.uni} fptr, flist;

// indirect call via pointer, with no knowledge of call targets
call{.uni} (ret-param), fptr, (param-list), fproto;
call{.uni} fptr, (param-list), fproto;
call{.uni} fptr, fproto;
Description

The call instruction stores the address of the next instruction, so execution can resume at that point after executing a ret instruction. A call is assumed to be divergent unless the .uni suffix is present, indicating that the call is guaranteed to be non-divergent, meaning that all threads in a warp have identical values for the guard predicate and call target.

For direct calls, the called location func must be a symbolic function name; for indirect calls, the called location fptr must be an address of a function held in a register. Input arguments and return values are optional. Arguments may be registers, immediate constants, or variables in .param space. Arguments are pass-by-value.

Indirect calls require an additional operand, flist or fproto, to communicate the list of potential call targets or the common function prototype of all call targets, respectively. In the first case, flist gives a complete list of potential call targets and the optimizing backend is free to optimize the calling convention. In the second case, where the complete list of potential call targets may not be known, the common function prototype is given and the call must obey the ABI's calling convention.

The flist operand is either the name of an array (call table) initialized to a list of function names; or a label associated with a .calltargets directive, which declares a list of potential call targets. In both cases the fptr register holds the address of a function listed in the call table or .calltargets list, and the call operands are type-checked against the type signature of the functions indicated by flist.

The fproto operand is the name of a label associated with a .callprototype directive. This operand is used when a complete list of potential targets is not known. The call operands are type-checked against the prototype, and code generation will follow the ABI calling convention. If a function that doesn't match the prototype is called, the behavior is undefined.

Call tables may be declared at module scope or local scope, in either the constant or global state space. The .calltargets and .callprototype directives must be declared within a function body. All functions must be declared prior to being referenced in a call table initializer or .calltargets directive.

PTX ISA Notes

Direct call introduced in PTX ISA version 1.0. Indirect call introduced in PTX ISA version 2.1.

Target ISA Notes

Direct call supported on all target architectures. Indirect call requires sm_20 or higher.

Examples
// examples of direct call
    call     init;    // call function 'init'
    call.uni g, (a);  // call function 'g' with parameter 'a'
@p  call     (d), h, (a, b);  // return value into register d

// call-via-pointer using jump table
.func (.reg .u32 rv) foo (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) bar (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) baz (.reg .u32 a, .reg .u32 b) ...

.global .u32 jmptbl[5] = { foo, bar, baz };
      ...
@p    ld.global.u32  %r0, [jmptbl+4];
@p    ld.global.u32  %r0, [jmptbl+8];
      call  (retval), %r0, (x, y), jmptbl;

// call-via-pointer using .calltargets directive
.func (.reg .u32 rv) foo (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) bar (.reg .u32 a, .reg .u32 b) ...
.func (.reg .u32 rv) baz (.reg .u32 a, .reg .u32 b) ...
      ...
@p    mov.u32  %r0, foo;
@q    mov.u32  %r0, baz;
Ftgt: .calltargets foo, bar, baz;
      call  (retval), %r0, (x, y), Ftgt;

// call-via-pointer using .callprototype directive
.func dispatch (.reg .u32 fptr, .reg .u32 idx)
{
...
Fproto: .callprototype _ (.param .u32 _, .param .u32 _);
      call  %fptr, (x, y), Fproto;
...

9.7.11.6. Control Flow Instructions: ret

ret

Return from function to instruction after call.

Syntax
ret{.uni};
Description

Return execution to caller's environment. A divergent return suspends threads until all threads are ready to return to the caller. This allows multiple divergent ret instructions.

A ret is assumed to be divergent unless the .uni suffix is present, indicating that the return is guaranteed to be non-divergent.

Any values returned from a function should be moved into the return parameter variables prior to executing the ret instruction.

A return instruction executed in a top-level entry routine will terminate thread execution.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    ret;
@p  ret;

9.7.11.7. Control Flow Instructions: exit

exit

Terminate a thread.

Syntax
exit;
Description

Ends execution of a thread.

As threads exit, barriers waiting on all threads are checked to see if the exiting threads are the only threads that have not yet made it to a barrier for all threads in the CTA. If the exiting threads are holding up the barrier, the barrier is released.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    exit;
@p  exit;

9.7.12. Parallel Synchronization and Communication Instructions

These instructions are:
  • bar
  • bar.warp.sync
  • membar
  • atom
  • red
  • vote
  • match.sync

9.7.12.1. Parallel Synchronization and Communication Instructions: bar, barrier

bar, barrier

Barrier synchronization.

Syntax
barrier.sync{.aligned}      a{, b};
barrier.arrive{.aligned}    a, b;

barrier.red.popc{.aligned}.u32  d, a{, b}, {!}c;
barrier.red.op{.aligned}.pred   p, a{, b}, {!}c;

bar.sync      a{, b};
bar.arrive    a, b;

bar.red.popc.u32  d, a{, b}, {!}c;
bar.red.op.pred   p, a{, b}, {!}c;

.op = { .and, .or };
Description

Performs barrier synchronization and communication within a CTA. Each CTA instance has sixteen barriers numbered 0..15.

Cooperative thread arrays use the barrier instruction for barrier synchronization and communication between threads.

Operands a, b, and d have type .u32; operands p and c are predicates. Source operand a specifies a logical barrier resource as an immediate constant or register with value 0 through 15.  Operand b specifies the number of threads participating in the barrier.  If no thread count is specified, all threads in the CTA participate in the barrier. When specifying a thread count, the value must be a multiple of the warp size. Note that a non-zero thread count is required for barrier.arrive.

Depending on operand b, either specified number of threads (in multiple of warp size) or all threads in the CTA participate in barrier instruction. The barrier instructions signal the arrival of the executing threads at the named barrier.

barrier instruction causes executing thread to wait for all non-exited threads from its warp and marks warps’ arrival at barrier. In addition to signaling its arrival at the barrier, the barrier.red and barrier.sync instructions causes executing thread to wait for non-exited threads of all other warps participating in the barrier to arrive. barrier.arrive does not cause executing thread to wait for threads of other participating warps.

When a barrier completes, the waiting threads are restarted without delay, and the barrier is reinitialized so that it can be immediately reused.

The barrier.sync or barrier.red or barrier.arrive instruction guarantees that when the barrier completes, prior memory accesses requested by this thread are performed relative to all threads participating in the barrier. The barrier.sync and barrier.red instruction further guarantees that no new memory access is requested by this thread before the barrier completes.

A memory read (e.g., by ld or atom) has been performed when the value read has been transmitted from memory and cannot be modified by another thread participating in the barrier. A memory write (e.g., by st, red or atom) has been performed when the value written has become visible to other threads participating in the barrier, that is, when the previous value can no longer be read.

barrier.red performs a reduction operation across threads. The c predicate (or its complement) from all threads in the CTA are combined using the specified reduction operator. Once the barrier count is reached, the final value is written to the destination register in all threads waiting at the barrier.

The reduction operations for barrier.red are population-count (.popc), all-threads-True (.and), and any-thread-True (.or). The result of .popc is the number of threads with a True predicate, while .and and .or indicate if all the threads had a True predicate or if any of the threads had a True predicate.

Instruction barrier has optional .aligned modifier. When specified, it indicates that all threads in CTA will execute the same barrier instruction. In conditionally executed code, an aligned barrier instruction should only be used if it is known that all threads in CTA evaluate the condition identically, otherwise behavior is undefined.

Different warps may execute different forms of the barrier instruction using the same barrier name and thread count. One example mixes barrier.sync and barrier.arrive to implement producer/consumer models. The producer threads execute barrier.arrive to announce their arrival at the barrier and continue execution without delay to produce the next value, while the consumer threads execute the barrier.sync to wait for a resource to be produced. The roles are then reversed, using a different barrier, where the producer threads execute a barrier.sync to wait for a resource to consumed, while the consumer threads announce that the resource has been consumed with barrier.arrive. Care must be taken to keep a warp from executing more barrier instructions than intended (barrier.arrive followed by any other barrier instruction to the same barrier) prior to the reset of the barrier. barrier.red should not be intermixed with barrier.sync or barrier.arrive using the same active barrier. Execution in this case is unpredictable.

bar.sync is equivalent to barrier.sync.aligned. bar.arrive is equivalent to barrier.arrive.aligned. bar.red is equivalent to barrier.red.aligned.

Note: For .target sm_6x or below,
  1. barrier instruction without .aligned modifier is equivalent to .aligned variant and has the same restrictions as of .aligned variant.
  2. All threads in warp (except for those have exited) must execute barrier instruction in convergence.
PTX ISA Notes

bar.sync without a thread count introduced in PTX ISA version 1.0.

Register operands, thread count, and bar.{arrive,red} introduced in PTX ISA version 2.0.

barrier instruction introduced in PTX ISA version 6.0.

Target ISA Notes

Register operands, thread count, and bar.{arrive,red} require sm_20 or higher.

Only bar.sync with an immediate barrier number is supported for sm_1x targets.

barrier instruction requires sm_30 or higher.

Examples
// Use bar.sync to arrive at a pre-computed barrier number and
// wait for all threads in CTA to also arrive: 
    st.shared [r0],r1;  // write my result to shared memory
    bar.sync  1;        // arrive, wait for others to arrive
    ld.shared r2,[r3];  // use shared results from other threads

// Use bar.sync to arrive at a pre-computed barrier number and 
// wait for fixed number of cooperating threads to arrive:
    #define CNT1 (8*12) // Number of cooperating threads

    st.shared [r0],r1;  // write my result to shared memory
    bar.sync  1, CNT1;  // arrive, wait for others to arrive
    ld.shared r2,[r3];  // use shared results from other threads

// Use bar.red.and to compare results across the entire CTA: 
    setp.eq.u32 p,r1,r2;     // p is True if r1==r2
    bar.red.and.pred r3,1,p; // r3=AND(p) forall threads in CTA

// Use bar.red.popc to compute the size of a group of threads 
// that have a specific condition True: 
    setp.eq.u32 p,r1,r2;     // p is True if r1==r2
    bar.red.popc.u32 r3,1,p; // r3=SUM(p) forall threads in CTA

/* Producer/consumer model. The producer deposits a value in
 * shared memory, signals that it is complete but does not wait
 * using bar.arrive, and begins fetching more data from memory. 
 * Once the data returns from memory, the producer must wait 
 * until the consumer signals that it has read the value from
 * the shared memory location. In the meantime, a consumer 
 * thread waits until the data is stored by the producer, reads 
 * it, and then signals that it is done (without waiting).
 */
    // Producer code places produced value in shared memory.
    st.shared   [r0],r1;
    bar.arrive  0,64;
    ld.global   r1,[r2];
    bar.sync    1,64;
    ...

    // Consumer code, reads value from shared memory
    bar.sync   0,64;
    ld.shared  r1,[r0];
    bar.arrive 1,64;
    ...

    // Examples of barrier.sync
    st.shared   [r0],r1;
    barrier.sync  0;
    ld.shared    r1, [r0];

9.7.12.2. Parallel Synchronization and Communication Instructions: bar.warp.sync

bar.warp.sync

Barrier synchronization for threads in a warp.

Syntax
bar.warp.sync      membermask;
Description

bar.warp.sync will cause executing thread to wait until all threads corresponding to membermask have executed a bar.warp.sync with the same membermask value before resuming execution.

Operand membermask specifies a 32-bit integer which is a mask indicating threads participating in barrier where the bit position corresponds to thread’s laneid.

The behavior of bar.warp.sync is undefined if the executing thread is not in the membermask.

bar.warp.sync also guarantee memory ordering among threads participating in barrier. Thus, threads within warp that wish to communicate via memory can store to memory, execute bar.warp.sync, and then safely read values stored by other threads in warp.

Note: For .target sm_6x or below, all threads in membermask must execute the same bar.warp.sync instruction in convergence, and only threads belonging to some membermask can be active when the bar.warp.sync instruction is executed. Otherwise, the behavior is undefined.
PTX ISA Notes

Introduced in PTX ISA version 6.0.

Target ISA Notes

Requires sm_30 or higher.

Examples
    st.shared.u32 [r0],r1;         // write my result to shared memory
    bar.warp.sync  0xffffffff;     // arrive, wait for others to arrive
    ld.shared.u32 r2,[r3];         // read results written by other threads

9.7.12.3. Parallel Synchronization and Communication Instructions: membar/fence

membar/fence

Enforce an ordering of memory operations.

Syntax
fence{.sem}.scope;
membar.level;

.sem =   {.sc, .acq_rel};
.scope = {.cta, .gpu, .sys};
.level = {.cta, .gl, .sys};
Description

The membar instruction guarantees that prior memory accesses requested by this thread (ld, st, atom and red instructions) are performed at the specified level, before later memory operations requested by this thread following the membar instruction. The level qualifier specifies the set of threads that may observe the ordering effect of this operation.

A memory read (e.g., by ld or atom) has been performed when the value read has been transmitted from memory and cannot be modified by another thread at the indicated level. A memory write (e.g., by st, red or atom) has been performed when the value written has become visible to other threads at the specified level, that is, when the previous value can no longer be read.

The fence instruction establishes an ordering between memory accesses requested by this thread (ld, st, atom and red instructions) as described in the Memory Consistency Model. The scope qualifier specifies the set of threads that may observe the ordering effect of this operation.

fence.acq_rel is a light-weight fence that is sufficient for memory synchronization in most programs. Instances of fence.acq_rel synchronize when combined with additional memory operations as described in acquire and release patterns in the Memory Consistency Model. If the optional .sem qualifier is absent, .acq_rel is assumed by default.

fence.sc is a slower fence that can restore sequential consistency when used in sufficient places, at the cost of performance. Instances of fence.sc with sufficient scope always synchronize by forming a total order per scope, determined at runtime. This total order can be constrained further by other synchronization in the program.

On sm_70 and higher membar is is a synonym for fence.sc1, and the membar levels cta, gl and sys are synonymous with the fence scopes cta, gpu and sys respectively.

1 The semantics of fence.sc introduced with sm_70 is a superset of the semantics of membar and the two are compatible; when executing on sm_70 or later architectures, membar acquires the full semantics of fence.sc.

PTX ISA Notes

membar.{cta,gl} introduced in PTX ISA version 1.4.

membar.sys introduced in PTX ISA version 2.0.

fence introdunced in PTX ISA version 6.0.

Target ISA Notes

membar.{cta,gl} supported on all target architectures.

membar.sys requires sm_20 or higher.

fence requires sm_70 or higher.

Examples
    membar.gl;
    membar.cta;
    membar.sys;
    
    fence.sc;

9.7.12.4. Parallel Synchronization and Communication Instructions: atom

atom

Atomic reduction operations for thread-to-thread communication.

Syntax
atom{.sem}{.scope}{.space}.op.type d, [a], b;
atom{.sem}{.scope}{.space}.op.type d, [a], b, c;

.space = { .global, .shared };
.sem =   { .relaxed, .acquire, .release, .acq_rel };
.scope = { .cta, .gpu, .sys };

.op =    { .and, .or, .xor,
           .cas, .exch,
           .add, .inc, .dec,
           .min, .max };
.type =  { .b32, .b64, .u32, .u64, .s32, .s64, .f32, .f64 };
Description

Atomically loads the original value at location a into destination register d, performs a reduction operation with operand b and the value in location a, and stores the result of the specified operation at location a, overwriting the original value. Operand a specifies a location in the specified state space. If no state space is given, perform the memory accesses using Generic Addressing. Atomic operations may be used only with .global and .shared spaces and with generic addressing, where the address points to .global or .shared space.

The optional .sem qualifier specifies a memory synchronizing effect as described in the Memory Consistency Model. If the .sem qualifier is absent, .relaxed is assumed by default.

The optional .scope qualifier specifies the set of threads that can directly observe the memory synchronizing effect of this operation, as described in the Memory Consistency Model.

Two atomic operations {atom or red} are performed atomically with respect to each other only if each operation specifies a scope that includes the other. When this condition is not met, each operation observes the other operation being performed as if it were split into a read followed by a dependent write.

If no scope is specified, the atomic operation is performed with .gpu scope.

For sm_6x and earlier architectures, atom operations on .shared state space do not guarantee atomicity with respect to normal store instructions to the same address. It is the programmer's responsibility to guarantee correctness of programs that use shared memory atomic instructions, e.g., by inserting barriers between normal stores and atomic operations to a common address, or by using atom.exch to store to locations accessed by other atomic operations.

Supported addressing modes for operand a are described in Addresses as Operands

The bit-size operations are .and, .or, .xor, .cas (compare-and-swap), and .exch (exchange).

The integer operations are .add, .inc, .dec, .min, .max. The .inc and .dec operations return a result in the range [0..b].

The floating-point operation .add operation rounds to nearest even. Current implementation of atom.add.f32 on global memory flushes subnormal inputs and results to sign-preserving zero; whereas atom.add.f32 on shared memory supports subnormal inputs and results and doesn't flush them to zero.

Semantics
atomic {
    d = *a;
    *a = (operation == cas) ? operation(*a, b, c)
                            : operation(*a, b);
}
where
    inc(r, s)  = (r >= s) ? 0 : r+1;
    dec(r, s)  = (r==0 || r > s)  ? s : r-1;
    exch(r, s) =  s;
    cas(r,s,t) = (r == s) ? t : r;
Notes

Simple reductions may be specified by using the bit bucket destination operand _.

PTX ISA Notes

32-bit atom.global introduced in PTX ISA version 1.1.

atom.shared and 64-bit atom.global.{add,cas,exch} introduced in PTX ISA 1.2.

atom.add.f32 and 64-bit atom.shared.{add,cas,exch} introduced in PTX ISA 2.0.

64-bit atom.{and,or,xor,min,max} introduced in PTX ISA 3.1.

atom.add.f64 introduced in PTX ISA 5.0.

.scope qualifier introduced in PTX ISA 5.0.

.sem qualifier introduced in PTX ISA version 6.0.

Target ISA Notes

atom.global requires sm_11 or higher.

atom.shared requires sm_12 or higher.

64-bit atom.global.{add,cas,exch} require sm_12 or higher.

64-bit atom.shared.{add,cas,exch} require sm_20 or higher.

64-bit atom.{and,or.xor,min,max} require sm_32 or higher.

atom.add.f32 requires sm_20 or higher.

atom.add.f64 requires sm_60 or higher.

.scope qualifier requires sm_60 or higher.

.sem qualifier requires sm_70 or higher.

Use of generic addressing requires sm_20 or higher.

Examples
    atom.global.add.s32  d,[a],1;
    atom.shared.max.u32  d,[x+4],0;
    @p  atom.global.cas.b32  d,[p],my_val,my_new_val;
    atom.global.sys.add.u32 d, [a], 1;

    atom.global.acquire.sys.inc.u32 ans, [gbl], %r0;

9.7.12.5. Parallel Synchronization and Communication Instructions: red

red

Reduction operations on global and shared memory.

Syntax
red{.sem}{.scope}{.space}.op.type [a], b;

.space = { .global, .shared };
.sem =   {.relaxed, .release};
.scope = {.cta, .gpu, .sys};

.op =    { .and, .or, .xor,
           .add, .inc, .dec,
           .min, .max };
.type =  { .b32, .b64, .u32, .u64, .s32, .s64, .f32, .f64 };
Description

Performs a reduction operation with operand b and the value in location a, and stores the result of the specified operation at location a, overwriting the original value. Operand a specifies a location in the specified state space. If no state space is given, perform the memory accesses using Generic Addressing. Atomic operations may be used only with .global and .shared spaces and with generic addressing, where the address points to .global or .shared space.

The optional .sem qualifier specifies a memory synchronizing effect as described in the Memory Consistency Model. If the .sem qualifier is absent, .relaxed is assumed by default.

The optional .scope qualifier specifies the set of threads that can directly observe the memory synchronizing effect of this operation, as described in the Memory Consistency Model.

Two atomic operations {atom or red} are performed atomically with respect to each other only if each operation specifies a scope that includes the other. When this condition is not met, each operation observes the other operation being performed as if it were split into a read followed by a dependent write.

If no scope is specified, the reduction operation is performed with .gpu scope.

For sm_6x and earlier architectures, red operations on .shared state space do not guarantee atomicity with respect to normal store instructions to the same address. It is the programmer's responsibility to guarantee correctness of programs that use shared memory reduction instructions, e.g., by inserting barriers between normal stores and reduction operations to a common address, or by using atom.exch to store to locations accessed by other reduction operations.

Supported addressing modes for operand a are described in Addresses as Operands

The bit-size operations are .and, .or, and .xor.

The integer operations are .add, .inc, .dec, .min, .max. The .inc and .dec operations return a result in the range [0..b].

The floating-point operation .add operation rounds to nearest even. Current implementation of red.add.f32 on global memory flushes subnormal inputs and results to sign-preserving zero; whereas red.add.f32 on shared memory supports subnormal inputs and results and doesn't flush them to zero.

Semantics
*a = operation(*a, b);

where
    inc(r, s) = (r >= s) ? 0 : r+1;
    dec(r, s) = (r==0 || r > s)  ? s : r-1;
PTX ISA Notes

Introduced in PTX ISA version 1.2.

red.add.f32 and red.shared.add.u64 introduced in PTX ISA 2.0.

64-bit red.{and,or,xor,min,max} introduced in PTX ISA 3.1.

red.add.f64 introduced in PTX ISA 5.0.

.scope qualifier introduced in PTX ISA 5.0.

.sem qualifier introduced in PTX ISA version 6.0.

Target ISA Notes

red.global requires sm_11 or higher

red.shared requires sm_12 or higher.

red.global.add.u64 requires sm_12 or higher.

red.shared.add.u64 requires sm_20 or higher.

64-bit red.{and,or.xor,min,max} require sm_32 or higher.

red.add.f32 requires sm_20 or higher.

red.add.f64 requires sm_60 or higher.

.scope qualifier requires sm_60 or higher.

.sem qualifier requires sm_70 or higher.

Use of generic addressing requires sm_20 or higher.

Examples
    red.global.add.s32  [a],1;
    red.shared.max.u32  [x+4],0;
    @p  red.global.and.b32  [p],my_val;
    red.global.sys.add.u32 [a], 1;

    red.global.acquire.sys.add.u32 [gbl], 1;

9.7.12.6. Parallel Synchronization and Communication Instructions: vote

vote

Vote across thread group.

Syntax
vote.mode.pred  d, {!}a;
vote.ballot.b32 d, {!}a;  // 'ballot' form, returns bitmask

.mode = { .all, .any, .uni };
Description

Performs a reduction of the source predicate across all active threads in a warp. The destination predicate value is the same across all threads in the warp.

The reduction modes are:
.all
True if source predicate is True for all active threads in warp. Negate the source predicate to compute .none.
.any
True if source predicate is True for some active thread in warp. Negate the source predicate to compute .not_all.
.uni
True if source predicate has the same value in all active threads in warp. Negating the source predicate also computes .uni.

In the ballot form, vote.ballot.b32 simply copies the predicate from each thread in a warp into the corresponding bit position of destination register d, where the bit position corresponds to the thread's lane id.

An inactive thread in warp will contribute a 0 for its entry when participating in vote.ballot.b32.

PTX ISA Notes

Introduced in PTX ISA version 1.2.

Target ISA Notes

vote requires sm_12 or higher.

vote.ballot.b32 requires sm_20 or higher.

Release Notes

Note that vote applies to threads in a single warp, not across an entire CTA.

Examples
    vote.all.pred    p,q;
    vote.uni.pred    p,q;
    vote.ballot.b32  r1,p;  // get 'ballot' across warp

9.7.12.7. Parallel Synchronization and Communication Instructions: vote.sync

vote.sync

Vote across thread group.

Syntax
vote.sync.mode.pred  d, {!}a, membermask;
vote.sync.ballot.b32 d, {!}a, membermask;  // 'ballot' form, returns bitmask

.mode = { .all, .any, .uni };
Description

vote.sync will cause executing thread to wait until all non-exited threads corresponding to membermask have executed vote.sync with the same qualifiers and same membermask value before resuming execution.

Operand membermask specifies a 32-bit integer which is a mask indicating threads participating in this instruction where the bit position corresponds to thread’s laneid.

vote.sync performs a reduction of the source predicate across all non-exited threads in membermask. The destination predicate value is the same across all threads in the membermask.

The reduction modes are:
.all
True if source predicate is True for all non-exited threads in membermask. Negate the source predicate to compute .none.
.any
True if source predicate is True for some thread in membermask. Negate the source predicate to compute .not_all.
.uni
True if source predicate has the same value in all non-exited threads in membermask. Negating the source predicate also computes .uni.

In the ballot form, vote.sync.ballot.b32 simply copies the predicate from each thread in membermask into the corresponding bit position of destination register d, where the bit position corresponds to the thread's lane id.

A thread not specified in membermask will contribute a 0 for its entry in vote.sync.ballot.b32.

The behavior of vote.sync is undefined if the executing thread is not in the membermask.

Note: For .target sm_6x or below, all threads in membermask must execute the same vote.sync instruction in convergence, and only threads belonging to some membermask can be active when the vote.sync instruction is executed. Otherwise, the behavior is undefined.
PTX ISA Notes

Introduced in PTX ISA version 6.0.

Target ISA Notes

Requires sm_30 or higher.

Examples
    vote.sync.all.pred    p,q,0xffffffff;
    vote.sync.ballot.b32  r1,p,0xffffffff;  // get 'ballot' across warp

9.7.12.8. Parallel Synchronization and Communication Instructions: match.sync

match.sync

Broadcast and compare a value across threads in warp.

Syntax
match.any.sync.type  d, a, membermask;
match.all.sync.type  d[|p], a, membermask;

.type = { .b32, .b64 };
Description

match.sync will cause executing thread to wait until all non-exited threads from membermask have executed match.sync with the same qualifiers and same membermask value before resuming execution.

Operand membermask specifies a 32-bit integer which is a mask indicating threads participating in this instruction where the bit position corresponds to thread’s laneid.

match.sync performs broadcast and compare of operand a across all non-exited threads in membermask and sets destination d and optional predicate p based on mode.

Operand a has instruction type and d has .b32 type.

Destination d is a 32-bit mask where bit position in mask corresponds to thread’s laneid.

The matching operation modes are:
.all
d is set to mask corresponding to non-exited threads in membermask if all non-exited threads in membermask have same value of operand a; otherwise d is set to 0. Optionally predicate p is set to true if all non-exited threads in membermask have same value of operand a; otherwise p is set to false.
.any
d is set to mask of non-exited threads in membermask that have same value of operand a.

The behavior of match.sync is undefined if the executing thread is not in the membermask.

PTX ISA Notes

Introduced in PTX ISA version 6.0.

Target ISA Notes

Requires sm_70 or higher.

Release Notes

Note that match.sync applies to threads in a single warp, not across an entire CTA.

Examples
    match.any.sync.b32    d, a, 0xffffffff;
    match.all.sync.b64    d|p, a, mask;

9.7.13. Warp Level Matrix Multiply-Accumulate Instructions

The warp-level matrix multiply and accumulate (wmma) operation has the following form:

D = A * B + C

where D and C are called accumulators and may refer to the same matrix.

This warp-level computation is performed collectively by all threads in the warp as follows:

  • Load matrices A, B and C form memory into registers using the wmma.load operation. When the operation completes, the destination registers in each thread hold a fragment of the loaded matrix.
  • Perform the matrix multiply and accumulate operation using the wmma.mma operation on the loaded matrices. When the operation completes, the destination registers in each thread hold a fragment of the result matrix returned by the wmma.mma operation.
  • Store result Matrix D back to memory using the wmma.store operation. Alternately, result matrix D can also be used as argument C for a subsequent wmma.mma operation.
Preview Feature

wmma is introduced in PTX ISA version 6.0 as a preview only. All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.

9.7.13.1. Matrix Shape

The wmma operations support a limited set of shapes for the operand matrices A, B and C. The shapes of all three matrix operands are collectively described by the tuple MxNxK, where A is an MxK matrix, B is a KxN matrix, while C and D are MxN matrices.

The current implementation supports the matrix shape 16x16x16, which is compactly represented as m16n16k16 in the instruction syntax.

9.7.13.2. Matrix Fragments

Each thread in the warp holds a fragment of the matrix. The distribution of fragments loaded by the threads in a warp is unspecified, and hence the identity of the fragment within the matrix is also unspecified. The fragment returned by a wmma operation can be used as an operand for another wmma operation if the shape, layout and element type of the underlying matrix matches.

The shape of the fragment is determined by the shape and identity of the matrix as follows:

Table 29. Matrix Fragments
Shape Matrix A Matrix B Accumulator (f16) Accumulator (f32)
16x16x16 Eight elements of type .f16x2 Eight elements of type .f16x2 Four elements of type .f16x2 Eight elements of type .f32
Manipulating fragment contents

The contents of a matrix fragment can be manipulated by reading and writing to individual registers in the fragment, provided the following conditions are satisfied:

  • All registers are operated on uniformly across threads, using the same parameters.
  • The order of the matrix elements is not changed.

For example, if each register corresponding to a given matrix is multiplied by a uniform constant value, then the resulting matrix is simply the scaled version of the original matrix.

Note that type conversion between f16 and f32 accumulator fragments is not supported in either direction. The result is undefined even if the order of elements in the fragment remains unchanged.

9.7.13.3. Matrix Storage

Each matrix can be stored in memory with a row-major or column-major layout. In a row-major format, consecutive elements of each row are stored in contiguous memory locations, and the row is called the leading dimension of the matrix. In a column-major format, consecutive elements of each column are stored in contiguous memory locations and the column is called the leading dimension of the matrix.

Consecutive instances of the leading dimension (rows or columns) need not be stored contiguously in memory. The wmma.load and wmma.store operations accept an optional argument stride that specifies the offset from the beginning of each row (or column) to the next, in terms of matrix elements (and not bytes). For example, the matrix being accessed by a wmma operation may be a submatrix from a larger matrix stored in memory. This allows the programmer to compose a multiply-and-accumulate operation on matrices that are larger than the shapes supported by the wmma operation.

Default value for stride:

The default value of the stride is the size of the leading dimension of the matrix. For example, for an MxK matrix, the stride is K for a row-major layout and M for a column-major layout. In particular, the default strides for the supported matrix shapes are as follows:

Shape Matrix A Matrix B Accumulator
16x16x16 16 16 16

9.7.13.4. Warp-level Matrix Load Instruction: wmma.load

wmma.load

Collectively load a matrix from memory for WMMA

Syntax
wmma.load.a.sync.layout.shape{.ss}.f16 r, [p] {, stride};
wmma.load.b.sync.layout.shape{.ss}.f16 r, [p] {, stride};
wmma.load.c.sync.layout.shape{.ss}.type r, [p] {, stride};

.layout = {.row, .col};
.shape  = {.m16n16k16};
.ss     = {.global, .shared};
.type   = {.f16, .f32};
Description

Collectively load a matrix across all threads in a warp from the location indicated by address operand p in the specified state space into destination register r.

If no state space is given, perform the memory accesses using Generic Addressing. wmma.load operation may be used only with .global and .shared spaces and with generic addressing, where the address points to .global or .shared space.

The mutually exclusive qualifiers .a, .b and .c indicate whether matrix A, B or C is being loaded respectively for the wmma computation.

The destination operand r is a brace-enclosed vector expression that can hold the fragment returned by the load operation.

The shape qualifier indicates the dimensions of all the matrix arguments involved in the intended wmma computation.

The layout qualifier indicates whether the matrix to be loaded is stored in row-major or column-major format.

The address operand p must be 128-bit aligned. If p is not properly aligned, the resulting behavior is undefined.

stride is an optional 32-bit integer operand that provides an offset in terms of matrix elements between the start of consecutive instances of the leading dimension (rows or columns). The default value of stride is described in Matrix Storage and must be specified if the actual value is larger than the default. For example, if the matrix is a sub-matrix of a larger matrix, then the value of stride is the leading dimension of the larger matrix. Specifying a value lower than the default value results in undefined behavior.

The mandatory .sync qualifier indicates that wmma.load causes the executing thread to wait until all threads in the warp execute the same wmma.load instruction before resuming execution. The behavior of wmma.load is undefined if all threads do not use the same qualifiers and the same values of p and stride, or if any thread in the warp has exited.

wmma.load is treated as a weak memory operation in the Memory Consistency Model.

PTX ISA Notes

Introduced in PTX ISA version 6.0.

Preview feature: All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.

Target ISA Notes

Requires sm_70 or higher.

Examples
    // Load elements from f16 row-major matrix B 
    .func foo1 (.reg .u64 ptr) {
        .reg .b32 x<8>;
    
        wmma.load.b.sync.m16n16k16.row.f16 {x0,x1,x2,x3,x4,x5,x,x7}, [ptr];
        // Now use {x0, ..., x7} for the actual wmma.mma
    }
    
     // Load elements from f32 column-major matrix C and scale the values:
    .func foo2 (.reg .u64 ptr) {
        .reg .b32 x<8>;
     
        wmma.load.c.sync.m16n16k16.col.f32
                         {x0,x1,x2,x3,x4,x5,x6,x7}, [ptr];
     
        mul.f32 x0, x0, 0.1;
        // repeat for all registers x<8>;
        ...
        mul.f32 x7, x7, 0.1;
        // Now use {x0, ..., x7} for the actual wmma.mma
    }

9.7.13.5. Warp-level Matrix Load Instruction: wmma.store

wmma.store

Collectively store a matrix into memory for WMMA

Syntax
wmma.store.d.sync.layout.shape{.ss}.type [p], r {, stride};

.layout = {.row, .col};
.shape  = {.m16n16k16};
.ss     = {.global, .shared};
.type   = {.f16, .f32};
Description

Collectively store a matrix across all threads in a warp at the location indicated by address operand p in the specified state space from source register r.

If no state space is given, perform the memory accesses using Generic Addressing. wmma.load operation may be used only with .global and .shared spaces and with generic addressing, where the address points to .global or .shared space.

The source operand r is a brace-enclosed vector expression that matches the shape of the fragment expected by the store operation.

The shape qualifier indicates the dimensions of all the matrix arguments involved in the intended wmma computation.

The layout qualifier indicates whether the matrix to be loaded is stored in row-major or column-major format.

The address operand p must be 128-bit aligned. If p is not properly aligned, the resulting behavior is undefined.

stride is an optional 32-bit integer operand that provides an offset in terms of matrix elements between the start of consecutive instances of the leading dimension (rows or columns). The default value of stride is described in Matrix Storage and must be specified if the actual value is larger than the default. For example, if the matrix is a sub-matrix of a larger matrix, then the value of stride is the leading dimension of the larger matrix. Specifying a value lower than the default value results in undefined behavior.

The mandatory .sync qualifier indicates that wmma.store causes the executing thread to wait until all threads in the warp execute the same wmma.store before resuming execution. The behavior of wmma.store is undefined if all threads do not use the same qualifiers and the same values of p and stride, or if any thread in the warp has exited.

wmma.store is treated as a weak memory operation in the Memory Consistency Model.

PTX ISA Notes

Introduced in PTX ISA version 6.0.

Preview feature: All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.

Target ISA Notes

Requires sm_70 or higher.

Examples
    // Storing f16 elements computed by a wmma.mma 
    .func foo (.reg .u64 ptr) {
        .reg .b32 x<8>;
 
        wmma.mma.sync.m16n16k16.row.col.f32.f32
                      {d0, d1, d2, d3, d4, d5, d6, d7}, ...;
        wmma.store.d.sync.m16n16k16.row.f32
                      [ptr], {d0, d1, d2, d3, d4, d5, d6, d7};
    }

9.7.13.6. Warp-level Matrix Multiply-and-Accumulate Instruction: wmma.mma

wmma.store

Perform a single matrix multiply-and-accumulate operation across a warp

Syntax
wmma.mma.sync.alayout.blayout.shape.dtype.ctype{.satfinite} d, a, b, c;

.alayout = {.row, .col};
.blayout = {.row, .col};
.shape   = {.m16n16k16};
.ctype   = {.f16, .f32};
.dtype   = {.f16, .f32};
Description

Perform a warp-level matrix multiply-and-accumulate computation D = A * B + C using matrices A, B and C loaded in registers a, b and c respectively, and store the result matrix in register d. The register arguments a, b, c and d hold unspecified fragments of the corresponding matrices as described in Matrix Fragments

The qualifiers ctype and dtype indicate the data-type of the elements in the matrix C and D, which may be f16 or f32.

The qualifiers alayout and blayout must match the layout specified on the wmma.load instructions that produce the contents of operands a and b respectively.

The shape qualifier must match the shape qualifier used on the wmma.load instructions that produce the contents of all three input operands a, b and c respectively.

The destination operand d is a brace-enclosed vector expression that matches the shape of the fragment computed by the wmma.mma instruction.

The optional qualifier satfinite indicates the following numerical properties of all elements in the destination operand:

  • +Inf is stored as the maximum finite value for that type
  • -Inf is stored as the minimum finite value for that type
  • NaN is stored as a positive zero

Element-wise multiplication of matrix A and B is performed with at least single precision. When ctype or dtype is .f32, accumulation of the intermediate values is performed with at least single precision. When both ctype and dtype are specified as .f16, the accumulation is performed with at least half precision.

The accumulation order, rounding and handling of subnormal inputs is unspecified.

The mandatory .sync qualifier indicates that wmma.mma causes the executing thread to wait until all threads in the warp execute the same wmma.mma before resuming execution. The behavior of wmma.mma is undefined if all threads do not use the same qualifiers, or if any thread in the warp executing wmma.mma has exited.

PTX ISA Notes

Introduced in PTX ISA version 6.0.

Preview feature: All details are subject to change with no guarantees of backward compatibility on future PTX ISA versions or SM architectures.

Target ISA Notes

Requires sm_70 or higher.

Examples
    .global .f16 A[256], B[256], C[256], D[256];
    .func foo () {
        .reg .b32 a<8> b<8> c<8> d<8>;
     
        wmma.load.a.sync.m16n16k16.global.row.f16
                {a0, a1, a2, a3, a4, a5, a6, a7}, [A];
        wmma.load.b.sync.m16n16k16.global.col.f16
                {b0, b1, b2, b3, b4, b5, b6, b7}, [B];
     
        wmma.load.c.sync.m16n16k16.global.row.f32
                {c0, c1, c2, c3, c4, c5, c6, c7}, [C];
     
        wmma.mma.sync.m16n16k16.row.col.f32.f32
                {d0, d1, d2, d3, d4, d5, d6, d7},
                {a0, a1, a2, a3, a4, a5, a6, a7},
                {b0, b1, b2, b3, b4, b5, b6, b7},
                {c0, c1, c2, c3, c4, c5, c6, c7};
     
        wmma.store.sync.d.m16n16k16.global.col.f32
                [D], {d0, d1, d2, d3, d4, d5, d6, d7};
    }

9.7.14. Video Instructions

All video instructions operate on 32-bit register operands. However, the video instructions may be classified as either scalar or SIMD based on whether their core operation applies to one or multiple values.

The video instructions are:
  • vadd, vadd2, vadd4
  • vsub, vsub2, vsub4
  • vmad
  • vavrg2, vavrg4
  • vabsdiff, vabsdiff2, vabsdiff4
  • vmin, vmin2, vmin4
  • vmax, vmax2, vmax4
  • vshl
  • vshr
  • vset, vset2, vset4

9.7.15. Scalar Video Instructions

All scalar video instructions operate on 32-bit register operands. The scalar video instructions are:
  • vadd
  • vsub
  • vabsdiff
  • vmin
  • vmax
  • vshl
  • vshr
  • vmad
  • vset
The scalar video instructions execute the following stages:
  1. Extract and sign- or zero-extend byte, half-word, or word values from its source operands, to produce signed 33-bit input values.
  2. Perform a scalar arithmetic operation to produce a signed 34-bit result.
  3. Optionally clamp the result to the range of the destination type.
  4. Optionally perform one of the following:
    • apply a second operation to the intermediate result and a third operand, or
    • truncate the intermediate result to a byte or half-word value and merge into a specified position in the third operand to produce the final result.

The general format of scalar video instructions is as follows: 

// 32-bit scalar operation, with optional secondary operation
vop.dtype.atype.btype{.sat}        d, a{.asel}, b{.bsel};
vop.dtype.atype.btype{.sat}.secop  d, a{.asel}, b{.bsel}, c;

// 32-bit scalar operation, with optional data merge
vop.dtype.atype.btype{.sat}   d.dsel, a{.asel}, b{.bsel}, c;


.dtype = .atype = .btype = { .u32, .s32 };
.dsel  = .asel  = .bsel  = { .b0, .b1, .b2, .b3, .h0, .h1 };
.secop = { .add, .min, .max };

The source and destination operands are all 32-bit registers. The type of each operand (.u32 or .s32) is specified in the instruction type; all combinations of dtype, atype, and btype are valid. Using the atype/btype and asel/bsel specifiers, the input values are extracted and sign- or zero-extended internally to .s33 values. The primary operation is then performed to produce an .s34 intermediate result. The sign of the intermediate result depends on dtype.

The intermediate result is optionally clamped to the range of the destination type (signed or unsigned), taking into account the subword destination size in the case of optional data merging. 

.s33 optSaturate( .s34 tmp, Bool sat, Bool sign, Modifier dsel ) {
    if ( !sat )  return tmp;

    switch ( dsel ) {
        case .b0, .b1, .b2, .b3:
            if ( sign )  return CLAMP( tmp, S8_MAX, S8_MIN );
            else         return CLAMP( tmp, U8_MAX, U8_MIN );
        case .h0, .h1:
            if ( sign )  return CLAMP( tmp, S16_MAX, S16_MIN );
            else         return CLAMP( tmp, U16_MAX, U16_MIN );
        default:
            if ( sign )  return CLAMP( tmp, S32_MAX, S32_MIN );
            else         return CLAMP( tmp, U32_MAX, U32_MIN );
    }
}

This intermediate result is then optionally combined with the third source operand using a secondary arithmetic operation or subword data merge, as shown in the following pseudocode. The sign of the third operand is based on dtype. 

.s33 optSecOp(Modifier secop, .s33 tmp, .s33 c) {
    switch ( secop ) {
        .add:     return tmp + c;
        .min:     return MIN(tmp, c);
        .max      return MAX(tmp, c);
        default:  return tmp;
    }
}
.s33 optMerge( Modifier dsel, .s33 tmp, .s33 c ) {
    switch ( dsel ) {
        case .h0:  return ((tmp & 0xffff)        | (0xffff0000 & c);
        case .h1:  return ((tmp & 0xffff) << 16) | (0x0000ffff & c);
        case .b0:  return ((tmp & 0xff)          | (0xffffff00 & c);
        case .b1:  return ((tmp & 0xff) <<  8)   | (0xffff00ff & c);
        case .b2:  return ((tmp & 0xff) << 16)   | (0xff00ffff & c);
        case .b3:  return ((tmp & 0xff) << 24)   | (0x00ffffff & c);
        default:   return tmp;
    }
}

The lower 32-bits are then written to the destination operand.

9.7.15.1. Scalar Video Instructions: vadd, vsub, vabsdiff, vmin, vmax

vadd, vsub, vabsdiff, vmin, vmax

Integer byte/half-word/word addition/subtraction.

vabsdiff

Integer byte/half-word/word absolute value of difference.

vmin, vmax

Integer byte/half-word/word minimum/maximum.

Syntax
// 32-bit scalar operation, with optional secondary operation
vop.dtype.atype.btype{.sat}       d, a{.asel}, b{.bsel};
vop.dtype.atype.btype{.sat}.op2   d, a{.asel}, b{.bsel}, c;

// 32-bit scalar operation, with optional data merge
vop.dtype.atype.btype{.sat}  d.dsel, a{.asel}, b{.bsel}, c;

 vop   = { vadd, vsub, vabsdiff, vmin, vmax };
.dtype = .atype = .btype = { .u32, .s32 };
.dsel  = .asel  = .bsel  = { .b0, .b1, .b2, .b3, .h0, .h1 };
.op2   = { .add, .min, .max };
Description

Perform scalar arithmetic operation with optional saturate, and optional secondary arithmetic operation or subword data merge.

Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a, atype, asel );
tb = partSelectSignExtend( b, btype, bsel );

switch ( vop ) {
    case vadd:     tmp = ta + tb;
    case vsub:     tmp = ta - tb;
    case vabsdiff: tmp = | ta - tb |;
    case vmin:     tmp = MIN( ta, tb );
    case vmax:     tmp = MAX( ta, tb );
}
// saturate, taking into account destination type and merge operations
tmp = optSaturate( tmp, sat, isSigned(dtype), dsel );
d = optSecondaryOp( op2, tmp, c );  // optional secondary operation
d = optMerge( dsel, tmp, c );       // optional merge with c operand
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

vadd, vsub, vabsdiff, vmin, vmax require sm_20 or higher.

Examples
vadd.s32.u32.s32.sat      r1, r2.b0, r3.h0;
vsub.s32.s32.u32.sat      r1, r2.h1, r3.h1;
vabsdiff.s32.s32.s32.sat  r1.h0, r2.b0, r3.b2, c;
vmin.s32.s32.s32.sat.add  r1, r2, r3, c;

9.7.15.2. Scalar Video Instructions: vshl, vshr

vshl, vshr

Integer byte/half-word/word left/right shift.

Syntax
// 32-bit scalar operation, with optional secondary operation
vop.dtype.atype.u32{.sat}.mode       d, a{.asel}, b{.bsel};
vop.dtype.atype.u32{.sat}.mode.op2   d, a{.asel}, b{.bsel}, c;

// 32-bit scalar operation, with optional data merge
vop.dtype.atype.u32{.sat}.mode  d.dsel, a{.asel}, b{.bsel}, c;

 vop   = { vshl, vshr };
.dtype = .atype = { .u32, .s32 };
.mode  = { .clamp, .wrap };
.dsel  = .asel  = .bsel  = { .b0, .b1, .b2, .b3, .h0, .h1 };
.op2   = { .add, .min, .max };
Description
vshl
Shift a left by unsigned amount in b with optional saturate, and optional secondary arithmetic operation or subword data merge. Left shift fills with zero.
vshr
Shift a right by unsigned amount in b with optional saturate, and optional secondary arithmetic operation or subword data merge. Signed shift fills with the sign bit, unsigned shift fills with zero.
Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a,atype, asel );
tb = partSelectSignExtend( b, .u32, bsel );
if ( mode == .clamp  && tb > 32 )  tb = 32;
if ( mode == .wrap )                       tb = tb & 0x1f;
switch ( vop ){
   case vshl:  tmp = ta << tb;
   case vshr:  tmp = ta >> tb;
}
// saturate, taking into account destination type and merge operations
tmp = optSaturate( tmp, sat, isSigned(dtype), dsel );
d = optSecondaryOp( op2, tmp, c );  // optional secondary operation
d = optMerge( dsel, tmp, c );       // optional merge with c operand
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

vshl, vshr require sm_20 or higher.

Examples
vshl.s32.u32.u32.clamp  r1, r2, r3;
vshr.u32.u32.u32.wrap   r1, r2, r3.h1;

9.7.15.3. Scalar Video Instructions: vmad

vmad

Integer byte/half-word/word multiply-accumulate.

Syntax
// 32-bit scalar operation
vmad.dtype.atype.btype{.sat}{.scale}     d, {-}a{.asel}, {-}b{.bsel},
                                         {-}c;
vmad.dtype.atype.btype.po{.sat}{.scale}  d, a{.asel}, b{.bsel}, c;

.dtype = .atype = .btype = { .u32, .s32 };
.asel  = .bsel  = { .b0, .b1, .b2, .b3, .h0, .h1 };
.scale = { .shr7, .shr15 };
Description

Calculate (a*b) + c, with optional operand negates, plus one mode, and scaling.

The source operands support optional negation with some restrictions. Although PTX syntax allows separate negation of the a and b operands, internally this is represented as negation of the product (a*b). That is, (a*b) is negated if and only if exactly one of a or b is negated. PTX allows negation of either (a*b) or c.

The plus one mode (.po) computes (a*b) + c + 1, which is used in computing averages. Source operands may not be negated in .po mode.

The intermediate result of (a*b) is unsigned if atype and btype are unsigned and the product (a*b) is not negated; otherwise, the intermediate result is signed. Input c has the same sign as the intermediate result.

The final result is unsigned if the intermediate result is unsigned and c is not negated.

Depending on the sign of the a and b operands, and the operand negates, the following combinations of operands are supported for VMAD: 

   (u32 * u32) + u32  // intermediate unsigned; final unsigned
  -(u32 * u32) + s32  // intermediate   signed; final   signed
   (u32 * u32) - u32  // intermediate unsigned; final   signed
   (u32 * s32) + s32  // intermediate   signed; final   signed
  -(u32 * s32) + s32  // intermediate   signed; final   signed
   (u32 * s32) - s32  // intermediate   signed; final   signed
   (s32 * u32) + s32  // intermediate   signed; final   signed
  -(s32 * u32) + s32  // intermediate   signed; final   signed
   (s32 * u32) - s32  // intermediate   signed; final   signed
   (s32 * s32) + s32  // intermediate   signed; final   signed
  -(s32 * s32) + s32  // intermediate   signed; final   signed
   (s32 * s32) - s32  // intermediate   signed; final   signed

The intermediate result is optionally scaled via right-shift; this result is sign-extended if the final result is signed, and zero-extended otherwise.

The final result is optionally saturated to the appropriate 32-bit range based on the type (signed or unsigned) of the final result.

Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a, atype, asel );
tb = partSelectSignExtend( b, btype, bsel );
signedFinal = isSigned(atype) || isSigned(btype) ||
                                 (a.negate ^ b.negate) || c.negate; 
tmp[127:0] = ta * tb;

lsb = 0;
if ( .po )                  {              lsb = 1; } else
if ( a.negate ^ b.negate )  { tmp = ~tmp;  lsb = 1; } else
if ( c.negate )             { c   = ~c;    lsb = 1; }

c128[127:0] = (signedFinal) sext32( c ) : zext ( c );
tmp = tmp + c128 + lsb; 
switch( scale ) {
   case .shr7:   result = (tmp >>  7) & 0xffffffffffffffff;
   case .shr15:  result = (tmp >> 15) & 0xffffffffffffffff;
}
if ( .sat ) {
     if (signedFinal) result = CLAMP(result, S32_MAX, S32_MIN);
     else             result = CLAMP(result, U32_MAX, U32_MIN);
}
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

vmad requires sm_20 or higher.

Examples
vmad.s32.s32.u32.sat    r0, r1, r2, -r3;
vmad.u32.u32.u32.shr15  r0, r1.h0, r2.h0, r3;

9.7.15.4. Scalar Video Instructions: vset

vset

Integer byte/half-word/word comparison.

Syntax
// 32-bit scalar operation, with optional secondary operation
vset.atype.btype.cmp       d, a{.asel}, b{.bsel};
vset.atype.btype.cmp.op2   d, a{.asel}, b{.bsel}, c;

// 32-bit scalar operation, with optional data merge
vset.atype.btype.cmp  d.dsel, a{.asel}, b{.bsel}, c;

.atype = .btype = { .u32, .s32 };
.cmp   = { .eq, .ne, .lt, .le, .gt, .ge };
.dsel  = .asel  = .bsel  = { .b0, .b1, .b2, .b3, .h0, .h1 };
.op2   = { .add, .min, .max };
Description

Compare input values using specified comparison, with optional secondary arithmetic operation or subword data merge.

The intermediate result of the comparison is always unsigned, and therefore destination d and operand c are also unsigned.

Semantics
// extract byte/half-word/word and sign- or zero-extend
// based on source operand type
ta = partSelectSignExtend( a, atype, asel );
tb = partSelectSignExtend( b, btype, bsel );
tmp = compare( ta, tb, cmp ) ? 1 : 0;
d = optSecondaryOp( op2, tmp, c );    // optional secondary operation
d = optMerge( dsel, tmp, c );         // optional merge with c operand
PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

vset requires sm_20 or higher.

Examples
vset.s32.u32.lt    r1, r2, r3;
vset.u32.u32.ne    r1, r2, r3.h1;

9.7.16. SIMD Video Instructions

The SIMD video instructions operate on pairs of 16-bit values and quads of 8-bit values.

The SIMD video instructions are:
  • vadd2, vadd4
  • vsub2, vsub4
  • vavrg2, vavrg4
  • vabsdiff2, vabsdiff4
  • vmin2, vmin4
  • vmax2, vmax4
  • vset2, vset4
PTX includes SIMD video instructions for operation on pairs of 16-bit values and quads of 8-bit values. The SIMD video instructions execute the following stages:
  1. Form input vectors by extracting and sign- or zero-extending byte or half-word values from the source operands, to form pairs of signed 17-bit values.
  2. Perform a SIMD arithmetic operation on the input pairs.
  3. Optionally clamp the result to the appropriate signed or unsigned range, as determinted by the destination type.
  4. Optionally perform one of the following:
    1. perform a second SIMD merge operation, or
    2. apply a scalar accumulate operation to reduce the intermediate SIMD results to a single scalar.

The general format of dual half-word SIMD video instructions is as follows: 

// 2-way SIMD operation, with second SIMD merge or accumulate
vop2.dtype.atype.btype{.sat}{.add}  d{.mask}, a{.asel}, b{.bsel}, c;

.dtype = .atype = .btype = { .u32, .s32 };
.mask  = { .h0, .h1, .h10 };
.asel  = .bsel = { .hxy, where x,y are from { 0, 1, 2, 3 } };

The general format of quad byte SIMD video instructions is as follows: 

// 4-way SIMD operation, with second SIMD merge or accumulate
vop4.dtype.atype.btype{.sat}{.add}  d{.mask}, a{.asel}, b{.bsel}, c;

.dtype = .atype = .btype = { .u32, .s32 };
.mask  = { .b0,
           .b1, .b10
           .b2, .b20, .b21, .b210,
           .b3, .b30, .b31, .b310, .b32, .b320, .b321, .b3210 };
.asel = .bsel = .bxyzw, where x,y,z,w are from { 0, ..., 7 };

The source and destination operands are all 32-bit registers. The type of each operand (.u32 or .s32) is specified in the instruction type; all combinations of dtype, atype, and btype are valid. Using the atype/btype and asel/bsel specifiers, the input values are extracted and sign- or zero-extended internally to .s33 values. The primary operation is then performed to produce an .s34 intermediate result. The sign of the intermediate result depends on dtype.

The intermediate result is optionally clamped to the range of the destination type (signed or unsigned), taking into account the subword destination size in the case of optional data merging.

9.7.16.1. SIMD Video Instructions: vadd2, vsub2, vavrg2, vabsdiff2, vmin2, vmax2

vadd2, vsub2

Integer dual half-word SIMD addition/subtraction.

vavrg2

Integer dual half-word SIMD average.

vabsdiff2

Integer dual half-word SIMD absolute value of difference.

vmin2, vmax2

Integer dual half-word SIMD minimum/maximum.

Syntax
// SIMD instruction with secondary SIMD merge operation
vop2.dtype.atype.btype{.sat}  d{.mask}, a{.asel}, b{.bsel}, c;

// SIMD instruction with secondary accumulate operation
vop2.dtype.atype.btype.add  d{.mask}, a{.asel}, b{.bsel}, c;

 vop2  = { vadd2, vsub2, vavrg2, vabsdiff2, vmin2, vmax2 };
.dtype = .atype = .btype = { .u32, .s32 };
.mask  = { .h0, .h1, .h10 };  // defaults to .h10
.asel  = .bsel  = { .hxy, where x,y are from { 0, 1, 2, 3 } };
   .asel defaults to .h10
   .bsel defaults to .h32
Description

Two-way SIMD parallel arithmetic operation with secondary operation.

Elements of each dual half-word source to the operation are selected from any of the four half-words in the two source operands a and b using the asel and bsel modifiers.

The selected half-words are then operated on in parallel.

The results are optionally clamped to the appropriate range determined by the destination type (signed or unsigned). Saturation cannot be used with the secondary accumulate operation.

For instructions with a secondary SIMD merge operation:

  • For half-word positions indicated in mask, the selected half-word results are copied into destination d. For all other positions, the corresponding half-word from source operand c is copied to d.

For instructions with a secondary accumulate operation:

  • For half-word positions indicated in mask, the selected half-word results are added to operand c, producing a result in d.
Semantics
// extract pairs of half-words and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_2( a, b, .asel, .atype );
Vb = extractAndSignExt_2( a, b, .bsel, .btype );
Vc = extractAndSignExt_2( c );

for (i=0; i<2; i++) {
    switch ( vop2 ) {
       case vadd2:             t[i] = Va[i] + Vb[i];
       case vsub2:             t[i] = Va[i] - Vb[i];
       case vavrg2:            if ( ( Va[i] + Vb[i] ) >= 0 ) {
                                   t[i] = ( Va[i] + Vb[i] + 1 ) >> 1;
                               } else {
                                   t[i] = ( Va[i] + Vb[i] ) >> 1;
                               }
       case vabsdiff2:         t[i] = | Va[i] - Vb[i] |;
       case vmin2:             t[i] = MIN( Va[i], Vb[i] );
       case vmax2:             t[i] = MAX( Va[i], Vb[i] );
    }
    if (.sat) {
        if ( .dtype == .s32 )  t[i] = CLAMP( t[i], S16_MAX, S16_MIN );
        else                   t[i] = CLAMP( t[i], U16_MAX, U16_MIN );
    }
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
    d = c;
    for (i=0; i<2; i++) {  d += mask[i] ? t[i] : 0;  }
} else {
    d = 0;
    for (i=0; i<2; i++)  {  d |= mask[i] ? t[i] : Vc[i];  }
}
PTX ISA Notes

Introduced in PTX ISA version 3.0.

Target ISA Notes

vadd2, vsub2, varvg2, vabsdiff2, vmin2, vmax2 require sm_30 or higher.

Examples
vadd2.s32.s32.u32.sat  r1, r2, r3, r1;
vsub2.s32.s32.s32.sat  r1.h0, r2.h10, r3.h32, r1;
vmin2.s32.u32.u32.add  r1.h10, r2.h00, r3.h22, r1;

9.7.16.2. SIMD Video Instructions: vset2

vset2

Integer dual half-word SIMD comparison.

Syntax
// SIMD instruction with secondary SIMD merge operation
vset2.atype.btype.cmp  d{.mask}, a{.asel}, b{.bsel}, c;

// SIMD instruction with secondary accumulate operation
vset2.atype.btype.cmp.add  d{.mask}, a{.asel}, b{.bsel}, c;

.atype = .btype = { .u32, .s32 };
.cmp   = { .eq, .ne, .lt, .le, .gt, .ge };
.mask  = { .h0, .h1, .h10 };  // defaults to .h10
.asel  = .bsel  = { .hxy, where x,y are from { 0, 1, 2, 3 } };
   .asel defaults to .h10
   .bsel defaults to .h32
Description

Two-way SIMD parallel comparison with secondary operation.

Elements of each dual half-word source to the operation are selected from any of the four half-words in the two source operands a and b using the asel and bsel modifiers.

The selected half-words are then compared in parallel.

The intermediate result of the comparison is always unsigned, and therefore the half-words of destination d and operand c are also unsigned.

For instructions with a secondary SIMD merge operation:

  • For half-word positions indicated in mask, the selected half-word results are copied into destination d. For all other positions, the corresponding half-word from source operand b is copied to d.

For instructions with a secondary accumulate operation:

  • For half-word positions indicated in mask, the selected half-word results are added to operand c, producing a result in d.
Semantics
// extract pairs of half-words and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_2( a, b, .asel, .atype );
Vb = extractAndSignExt_2( a, b, .bsel, .btype );
Vc = extractAndSignExt_2( c );
for (i=0; i<2; i++) {
    t[i] = compare( Va[i], Vb[i], .cmp ) ? 1 : 0;
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
    d = c;
    for (i=0; i<2; i++) {  d += mask[i] ? t[i] : 0;  }
} else {
    d = 0;
    for (i=0; i<2; i++)  {  d |= mask[i] ? t[i] : Vc[i];  }
}
PTX ISA Notes

Introduced in PTX ISA version 3.0.

Target ISA Notes

vset2 requires sm_30 or higher.

Examples
vset2.s32.u32.lt      r1, r2, r3, r0;
vset2.u32.u32.ne.add  r1, r2, r3, r0;

9.7.16.3. SIMD Video Instructions: vadd4, vsub4, vavrg4, vabsdiff4, vmin4, vmax4

vadd4, vsub4

Integer quad byte SIMD addition/subtraction.

vavrg4

Integer quad byte SIMD average.

vabsdiff4

Integer quad byte SIMD absolute value of difference.

vmin4, vmax4

Integer quad byte SIMD minimum/maximum.

Syntax
// SIMD instruction with secondary SIMD merge operation
vop4.dtype.atype.btype{.sat}  d{.mask}, a{.asel}, b{.bsel}, c;

// SIMD instruction with secondary accumulate operation
vop4.dtype.atype.btype.add  d{.mask}, a{.asel}, b{.bsel}, c;
vop4  = { vadd4, vsub4, vavrg4, vabsdiff4, vmin4, vmax4 };

.dtype = .atype = .btype = { .u32, .s32 };
.mask  = { .b0,
           .b1, .b10
           .b2, .b20, .b21, .b210,
           .b3, .b30, .b31, .b310, .b32, .b320, .b321, .b3210 };
    defaults to .b3210
.asel = .bsel = .bxyzw, where x,y,z,w are from { 0, ..., 7 };
   .asel defaults to .b3210
   .bsel defaults to .b7654
Description

Four-way SIMD parallel arithmetic operation with secondary operation.

Elements of each quad byte source to the operation are selected from any of the eight bytes in the two source operands a and b using the asel and bsel modifiers.

The selected bytes are then operated on in parallel.

The results are optionally clamped to the appropriate range determined by the destination type (signed or unsigned). Saturation cannot be used with the secondary accumulate operation.

For instructions with a secondary SIMD merge operation:

  • For byte positions indicated in mask, the selected byte results are copied into destination d. For all other positions, the corresponding byte from source operand c is copied to d.

For instructions with a secondary accumulate operation:

  • For byte positions indicated in mask, the selected byte results are added to operand c, producing a result in d.
Semantics
// extract quads of bytes and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_4( a, b, .asel, .atype );
Vb = extractAndSignExt_4( a, b, .bsel, .btype );
Vc = extractAndSignExt_4( c );
for (i=0; i<4; i++) {
    switch ( vop4 ) {
        case vadd4:            t[i] = Va[i] + Vb[i];
        case vsub4:            t[i] = Va[i] - Vb[i];
        case vavrg4:           if ( ( Va[i] + Vb[i] ) >= 0 ) {
                                   t[i] = ( Va[i] + Vb[i] + 1 ) >> 1;
                               } else {
                                   t[i] = ( Va[i] + Vb[i] ) >> 1;
                               }
        case vabsdiff4:        t[i] = | Va[i] - Vb[i] |;
        case vmin4:            t[i] = MIN( Va[i], Vb[i] );
        case vmax4:            t[i] = MAX( Va[i], Vb[i] );
    }
    if (.sat) {
        if ( .dtype == .s32 )  t[i] = CLAMP( t[i], S8_MAX, S8_MIN );
        else                   t[i] = CLAMP( t[i], U8_MAX, U8_MIN );
    }
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
    d = c;
    for (i=0; i<4; i++) {  d += mask[i] ? t[i] : 0;  }
} else {
    d = 0;
    for (i=0; i<4; i++)  {  d |= mask[i] ? t[i] : Vc[i];  }
}
PTX ISA Notes

Introduced in PTX ISA version 3.0.

Target ISA Notes

vadd4, vsub4, varvg4, vabsdiff4, vmin4, vmax4 require sm_30 or higher.

Examples
vadd4.s32.s32.u32.sat  r1, r2, r3, r1;
vsub4.s32.s32.s32.sat  r1.b0, r2.b3210, r3.b7654, r1;
vmin4.s32.u32.u32.add  r1.b00, r2.b0000, r3.b2222, r1;

9.7.16.4. SIMD Video Instructions: vset4

vset4

Integer quad byte SIMD comparison.

Syntax
// SIMD instruction with secondary SIMD merge operation
vset4.atype.btype.cmp  d{.mask}, a{.asel}, b{.bsel}, c;

// SIMD instruction with secondary accumulate operation
vset4.atype.btype.cmp.add  d{.mask}, a{.asel}, b{.bsel}, c;

.atype = .btype = { .u32, .s32 };
.cmp   = { .eq, .ne, .lt, .le, .gt, .ge };
.mask  = { .b0,
           .b1, .b10
           .b2, .b20, .b21, .b210,
           .b3, .b30, .b31, .b310, .b32, .b320, .b321, .b3210 };
    defaults to .b3210
.asel = .bsel = .bxyzw, where x,y,z,w are from { 0, ..., 7 };
   .asel defaults to .b3210
   .bsel defaults to .b7654
Description

Four-way SIMD parallel comparison with secondary operation.

Elements of each quad byte source to the operation are selected from any of the eight bytes in the two source operands a and b using the asel and bsel modifiers.

The selected bytes are then compared in parallel.

The intermediate result of the comparison is always unsigned, and therefore the bytes of destination d and operand c are also unsigned.

For instructions with a secondary SIMD merge operation:

  • For byte positions indicated in mask, the selected byte results are copied into destination d. For all other positions, the corresponding byte from source operand b is copied to d.

For instructions with a secondary accumulate operation:

  • For byte positions indicated in mask, the selected byte results are added to operand c, producing a result in d.
Semantics
// extract quads of bytes and sign- or zero-extend
// based on operand type
Va = extractAndSignExt_4( a, b, .asel, .atype );
Vb = extractAndSignExt_4( a, b, .bsel, .btype );
Vc = extractAndSignExt_4( c );
for (i=0; i<4; i++) {
    t[i] = compare( Va[i], Vb[i], cmp ) ? 1 : 0;
}
// secondary accumulate or SIMD merge
mask = extractMaskBits( .mask );
if (.add) {
    d = c;
    for (i=0; i<4; i++) {  d += mask[i] ? t[i] : 0;  }
} else {
    d = 0;
    for (i=0; i<4; i++)  {  d |= mask[i] ? t[i] : Vc[i];  }
}
PTX ISA Notes

Introduced in PTX ISA version 3.0.

Target ISA Notes

vset4 requires sm_30 or higher.

Examples
vset4.s32.u32.lt      r1, r2, r3, r0;
vset4.u32.u32.ne.max  r1, r2, r3, r0;

9.7.17. Miscellaneous Instructions

The Miscellaneous instructions are:
  • trap
  • brkpt
  • pmevent

9.7.17.1. Miscellaneous Instructions: trap

trap

Perform trap operation.

Syntax
trap;
Description

Abort execution and generate an interrupt to the host CPU.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples
    trap;
@p  trap;

9.7.17.2. Miscellaneous Instructions: brkpt

brkpt

Breakpoint.

Syntax
brkpt;
Description

Suspends execution.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

brkpt requires sm_11 or higher.

Examples
    brkpt;
@p  brkpt;

9.7.17.3. Miscellaneous Instructions: pmevent

pmevent

Trigger one or more Performance Monitor events.

Syntax
pmevent       a;    // trigger a single performance monitor event
pmevent.mask  a;    // trigger one or more performance monitor events
Description

Triggers one or more of a fixed number of performance monitor events, with event index or mask specified by immediate operand a.

pmevent (without modifier .mask) triggers a single performance monitor event indexed by immediate operand a, in the range 0..15.

pmevent.mask triggers one or more of the performance monitor events. Each bit in the 16-bit immediate operand a controls an event.

Programmatic performance moniter events may be combined with other hardware events using Boolean functions to increment one of the four performance counters. The relationship between events and counters is programmed via API calls from the host.

Notes

Currently, there are sixteen performance monitor events, numbered 0 through 15.

PTX ISA Notes

pmevent introduced in PTX ISA version 1.4.

pmevent.mask introduced in PTX ISA version 3.0.

Target ISA Notes
pmevent supported on all target architectures.

pmevent.mask requires sm_20 or higher.

Examples
    pmevent      1;
@p  pmevent      7;
@q  pmevent.mask 0xff;

10. Special Registers

PTX includes a number of predefined, read-only variables, which are visible as special registers and accessed through mov or cvt instructions.

The special registers are:
  • %tid
  • %ntid
  • %laneid
  • %warpid
  • %nwarpid
  • %ctaid
  • %nctaid
  • %smid
  • %nsmid
  • %gridid
  • %lanemask_eq, %lanemask_le, %lanemask_lt, %lanemask_ge, %lanemask_gt
  • %clock, %clock_hi, %clock64
  • %pm0, ..., %pm7
  • %pm0_64, ..., %pm7_64
  • %envreg0, ..., %envreg31
  • %total_smem_size
  • %dynamic_smem_size

10.1. Special Registers: %tid

%tid

Thread identifier within a CTA.

Syntax (predefined)

.sreg .v4 .u32 %tid;                  // thread id vector
.sreg .u32 %tid.x, %tid.y, %tid.z;    // thread id components

Description

A predefined, read-only, per-thread special register initialized with the thread identifier within the CTA. The %tid special register contains a 1D, 2D, or 3D vector to match the CTA shape; the %tid value in unused dimensions is 0. The fourth element is unused and always returns zero. The number of threads in each dimension are specified by the predefined special register %ntid.

Every thread in the CTA has a unique %tid.

%tid component values range from 0 through %ntid-1 in each CTA dimension.

%tid.y == %tid.z == 0 in 1D CTAs. %tid.z == 0 in 2D CTAs.

It is guaranteed that:

0  <=  %tid.x <  %ntid.x
0  <=  %tid.y <  %ntid.y
0  <=  %tid.z <  %ntid.z

PTX ISA Notes

Introduced in PTX ISA version 1.0 with type .v4.u16.

Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit mov and cvt instructions may be used to read the lower 16-bits of each component of %tid.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u32      %r1,%tid.x;  // move tid.x to %rh

    // legacy code accessing 16-bit components of %tid
    mov.u16      %rh,%tid.x;
    cvt.u32.u16  %r2,%tid.z;  // zero-extend tid.z to %r2

10.2. Special Registers: %ntid

%ntid

Number of thread IDs per CTA.

Syntax (predefined)

.sreg .v4 .u32 %ntid;                   // CTA shape vector
.sreg .u32 %ntid.x, %ntid.y, %ntid.z;   // CTA dimensions

Description

A predefined, read-only special register initialized with the number of thread ids in each CTA dimension. The %ntid special register contains a 3D CTA shape vector that holds the CTA dimensions. CTA dimensions are non-zero; the fourth element is unused and always returns zero. The total number of threads in a CTA is (%ntid.x * %ntid.y * %ntid.z). 

%ntid.y == %ntid.z == 1 in 1D CTAs.
%ntid.z ==1 in 2D CTAs.

Maximum values of %ntid.{x,y,z} are as follows:

.target architecture %ntid.x %ntid.y %ntid.z
sm_1x 512 512 64
sm_20, sm_3x, sm_5x, sm_6x 1024 1024 64

PTX ISA Notes

Introduced in PTX ISA version 1.0 with type .v4.u16.

Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit mov and cvt instructions may be used to read the lower 16-bits of each component of %ntid.

Target ISA Notes

Supported on all target architectures.

Examples

    // compute unified thread id for 2D CTA
    mov.u32  %r0,%tid.x;
    mov.u32  %h1,%tid.y;
    mov.u32  %h2,%ntid.x;
    mad.u32  %r0,%h1,%h2,%r0;

    mov.u16  %rh,%ntid.x;      // legacy code

10.3. Special Registers: %laneid

%laneid

Lane Identifier.

Syntax (predefined)

.sreg .u32 %laneid;

Description

A predefined, read-only special register that returns the thread's lane within the warp. The lane identifier ranges from zero to WARP_SZ-1.

PTX ISA Notes

Introduced in PTX ISA version 1.3.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u32  %r, %laneid;

10.4. Special Registers: %warpid

%warpid

Warp identifier.

Syntax (predefined)

.sreg .u32 %warpid;

Description

A predefined, read-only special register that returns the thread's warp identifier. The warp identifier provides a unique warp number within a CTA but not across CTAs within a grid. The warp identifier will be the same for all threads within a single warp.

Note that %warpid is volatile and returns the location of a thread at the moment when read, but its value may change during execution, e.g., due to rescheduling of threads following preemption. For this reason, %ctaid and %tid should be used to compute a virtual warp index if such a value is needed in kernel code; %warpid is intended mainly to enable profiling and diagnostic code to sample and log information such as work place mapping and load distribution.

PTX ISA Notes

Introduced in PTX ISA version 1.3.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u32  %r, %warpid;

10.5. Special Registers: %nwarpid

%nwarpid

Number of warp identifiers.

Syntax (predefined)

.sreg .u32 %nwarpid;

Description

A predefined, read-only special register that returns the maximum number of warp identifiers.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%nwarpid requires sm_20 or higher.

Examples

mov.u32  %r, %nwarpid;

10.6. Special Registers: %ctaid

%ctaid

CTA identifier within a grid.

Syntax (predefined)

.sreg .v4 .u32 %ctaid;                      // CTA id vector
.sreg .u32 %ctaid.x, %ctaid.y, %ctaid.z;    // CTA id components

Description

A predefined, read-only special register initialized with the CTA identifier within the CTA grid. The %ctaid special register contains a 1D, 2D, or 3D vector, depending on the shape and rank of the CTA grid. The fourth element is unused and always returns zero.

It is guaranteed that: 

0  <=  %ctaid.x <  %nctaid.x
0  <=  %ctaid.y <  %nctaid.y
0  <=  %ctaid.z <  %nctaid.z

PTX ISA Notes

Introduced in PTX ISA version 1.0 with type .v4.u16.

Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit mov and cvt instructions may be used to read the lower 16-bits of each component of %ctaid.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u32  %r0,%ctaid.x;
    mov.u16  %rh,%ctaid.y;   // legacy code

10.7. Special Registers: %nctaid

%nctaid

Number of CTA ids per grid.

Syntax (predefined)

.sreg .v4 .u32 %nctaid                      // Grid shape vector
.sreg .u32 %nctaid.x,%nctaid.y,%nctaid.z;   // Grid dimensions

Description

A predefined, read-only special register initialized with the number of CTAs in each grid dimension. The %nctaid special register contains a 3D grid shape vector, with each element having a value of at least 1. The fourth element is unused and always returns zero.

Maximum values of %nctaid.{x,y,z} are as follows:

.target architecture %nctaid.x %nctaid.y %nctaid.z
sm_1x, sm_20 65535 65535 65535
sm_3x, sm_5x, sm_6x 231 -1 65535 65535

PTX ISA Notes

Introduced in PTX ISA version 1.0 with type .v4.u16.

Redefined as type .v4.u32 in PTX ISA version 2.0. For compatibility with legacy PTX code, 16-bit mov and cvt instructions may be used to read the lower 16-bits of each component of %nctaid.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u32  %r0,%nctaid.x;
    mov.u16  %rh,%nctaid.x;     // legacy code

10.8. Special Registers: %smid

%smid

SM identifier.

Syntax (predefined)

.sreg .u32 %smid;

Description

A predefined, read-only special register that returns the processor (SM) identifier on which a particular thread is executing. The SM identifier ranges from 0 to %nsmid-1. The SM identifier numbering is not guaranteed to be contiguous.

Notes

Note that %smid is volatile and returns the location of a thread at the moment when read, but its value may change during execution, e.g. due to rescheduling of threads following preemption. %smid is intended mainly to enable profiling and diagnostic code to sample and log information such as work place mapping and load distribution.

PTX ISA Notes

Introduced in PTX ISA version 1.3.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u32  %r, %smid;

10.9. Special Registers: %nsmid

%nsmid

Number of SM identifiers.

Syntax (predefined)

.sreg .u32 %nsmid;

Description

A predefined, read-only special register that returns the maximum number of SM identifiers. The SM identifier numbering is not guaranteed to be contiguous, so %nsmid may be larger than the physical number of SMs in the device.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%nsmid requires sm_20 or higher.

Examples

    mov.u32  %r, %nsmid;

10.10. Special Registers: %gridid

%gridid

Grid identifier.

Syntax (predefined)

.sreg .u64 %gridid;

Description

A predefined, read-only special register initialized with the per-grid temporal grid identifier. The %gridid is used by debuggers to distinguish CTAs within concurrent (small) CTA grids.

During execution, repeated launches of programs may occur, where each launch starts a grid-of-CTAs. This variable provides the temporal grid launch number for this context.

For sm_1x targets, %gridid is limited to the range [0..216-1]. For sm_20, %gridid is limited to the range [0..232-1]. sm_30 supports the entire 64-bit range.

PTX ISA Notes

Introduced in PTX ISA version 1.0 as type .u16.

Redefined as type .u32 in PTX ISA version 1.3.

Redefined as type .u64 in PTX ISA version 3.0.

For compatibility with legacy PTX code, 16-bit and 32-bit mov and cvt instructions may be used to read the lower 16-bits or 32-bits of each component of %gridid.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.u64  %s, %gridid;  // 64-bit read of %gridid
    mov.u32  %r, %gridid;  // legacy code with 32-bit %gridid

10.11. Special Registers: %lanemask_eq

%lanemask_eq

32-bit mask with bit set in position equal to the thread's lane number in the warp.

Syntax (predefined)

.sreg .u32 %lanemask_eq;

Description

A predefined, read-only special register initialized with a 32-bit mask with a bit set in the position equal to the thread's lane number in the warp.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%lanemask_eq requires sm_20 or higher.

Examples

    mov.u32     %r, %lanemask_eq;

10.12. Special Registers: %lanemask_le

%lanemask_le

32-bit mask with bits set in positions less than or equal to the thread's lane number in the warp.

Syntax (predefined)

.sreg .u32 %lanemask_le;

Description

A predefined, read-only special register initialized with a 32-bit mask with bits set in positions less than or equal to the thread's lane number in the warp.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%lanemask_le requires sm_20 or higher.

Examples

    mov.u32     %r, %lanemask_le

10.13. Special Registers: %lanemask_lt

%lanemask_lt

32-bit mask with bits set in positions less than the thread's lane number in the warp.

Syntax (predefined)

.sreg .u32 %lanemask_lt;

Description

A predefined, read-only special register initialized with a 32-bit mask with bits set in positions less than the thread's lane number in the warp.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%lanemask_lt requires sm_20 or higher.

Examples

    mov.u32     %r, %lanemask_lt;

10.14. Special Registers: %lanemask_ge

%lanemask_ge

32-bit mask with bits set in positions greater than or equal to the thread's lane number in the warp.

Syntax (predefined)

.sreg .u32 %lanemask_ge;

Description

A predefined, read-only special register initialized with a 32-bit mask with bits set in positions greater than or equal to the thread's lane number in the warp.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%lanemask_ge requires sm_20 or higher.

Examples

    mov.u32     %r, %lanemask_ge;

10.15. Special Registers: %lanemask_gt

%lanemask_gt

32-bit mask with bits set in positions greater than the thread's lane number in the warp.

Syntax (predefined)

.sreg .u32 %lanemask_gt;

Description

A predefined, read-only special register initialized with a 32-bit mask with bits set in positions greater than the thread's lane number in the warp.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%lanemask_gt requires sm_20 or higher.

Examples

    mov.u32     %r, %lanemask_gt;

10.16. Special Registers: %clock, %clock_hi

%clock, %clock_hi

%clock
A predefined, read-only 32-bit unsigned cycle counter.
%clock_hi
The upper 32-bits of %clock64 special register.

Syntax (predefined)

.sreg .u32 %clock;
.sreg .u32 %clock_hi;

Description

Special register %clock and %clock_hi are unsigned 32-bit read-only cycle counters that wrap silently.

PTX ISA Notes

%clock introduced in PTX ISA version 1.0.

%clock_hi introduced in PTX ISA version 5.0.

Target ISA Notes

%clock supported on all target architectures.

%clock_hi requires sm_20 or higher.

Examples

    mov.u32 r1,%clock;
    mov.u32 r2, %clock_hi;

10.17. Special Registers: %clock64

%clock64

A predefined, read-only 64-bit unsigned cycle counter.

Syntax (predefined)

.sreg .u64 %clock64;

Description

Special register %clock64 is an unsigned 64-bit read-only cycle counter that wraps silently.

Notes

The lower 32-bits of %clock64 are identical to %clock.

The upper 32-bits of %clock64 are identical to %clock_hi.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

%clock64 requires sm_20 or higher.

Examples

    mov.u64  r1,%clock64;

10.18. Special Registers: %pm0..%pm7

%pm0..%pm7

Performance monitoring counters.

Syntax (predefined)

.sreg .u32 %pm<8>;

Description

Special registers %pm0..%pm7 are unsigned 32-bit read-only performance monitor counters. Their behavior is currently undefined.

PTX ISA Notes

%pm0..%pm3 introduced in PTX ISA version 1.3.

%pm4..%pm7 introduced in PTX ISA version 3.0.

Target ISA Notes

%pm0..%pm3 supported on all target architectures.

%pm4..%pm7 require sm_20 or higher.

Examples

    mov.u32  r1,%pm0;
    mov.u32  r1,%pm7;

10.19. Special Registers: %pm0_64..%pm7_64

%pm0_64..%pm7_64

64 bit Performance monitoring counters.

Syntax (predefined)

.sreg .u64 %pm0_64; 
.sreg .u64 %pm1_64;
.sreg .u64 %pm2_64;
.sreg .u64 %pm3_64;
.sreg .u64 %pm4_64;
.sreg .u64 %pm5_64;
.sreg .u64 %pm6_64;
.sreg .u64 %pm7_64;

Description

Special registers %pm0_64..%pm7_64 are unsigned 64-bit read-only performance monitor counters. Their behavior is currently undefined.

Notes

The lower 32bits of %pm0_64..%pm7_64 are identical to %pm0..%pm7.

PTX ISA Notes

%pm0_64..%pm7_64 introduced in PTX ISA version 4.0.

Target ISA Notes

%pm0_64..%pm7_64 require sm_50 or higher.

Examples

    mov.u32  r1,%pm0_64;
    mov.u32  r1,%pm7_64;

10.20. Special Registers: %envreg<32>

%envreg<32>

Driver-defined read-only registers.

Syntax (predefined)

.sreg .b32 %envreg<32>;

Description

A set of 32 pre-defined read-only registers used to capture execution environment of PTX program outside of PTX virtual machine. These registers are initialized by the driver prior to kernel launch and can contain cta-wide or grid-wide values.

Precise semantics of these registers is defined in the driver documentation.

PTX ISA Notes

Introduced in PTX ISA version 2.1.

Target ISA Notes

Supported on all target architectures.

Examples

    mov.b32      %r1,%envreg0;  // move envreg0 to %r1

10.21. Special Registers: %globaltimer, %globaltimer_lo, %globaltimer_hi

%globaltimer, %globaltimer_lo, %globaltimer_hi

%globaltimer
A predefined, 64-bit global nanosecond timer.
%globaltimer_lo
The lower 32-bits of %globaltimer.
%globaltimer_hi
The upper 32-bits of %globaltimer.

Syntax (predefined)

.sreg .u64 %globaltimer;
.sreg .u32 %globaltimer_lo, %globaltimer_hi;

Description

Special registers intended for use by NVIDIA tools. The behavior is target-specific and may change or be removed in future GPUs. When JIT-compiled to other targets, the value of these registers is unspecified.

PTX ISA Notes

Introduced in PTX ISA version 3.1.

Target ISA Notes

Requires target sm_30 or higher.

Examples

    mov.u64  r1,%globaltimer;

10.22. Special Registers: %total_smem_size

%total_smem_size

Total size of shared memory used by a CTA of a kernel.

Syntax (predefined)

.sreg .u32 %total_smem_size;

Description

A predefined, read-only special register initialized with total size of shared memory allocated (statically and dynamically) for the CTA of a kernel at launch time.

Size is returned in multiples of shared memory allocation unit size supported by target architecture.

Allocation unit values are as follows:

Target architecture Shared memory allocation unit size
sm_2x 128 bytes
sm_3x, sm_5x, sm_6x 256 bytes

PTX ISA Notes

Introduced in PTX ISA version 4.1.

Target ISA Notes

Requires sm_20 or higher.

Examples

    mov.u32  %r, %total_smem_size;

10.23. Special Registers: %dynamic_smem_size

%dynamic_smem_size

Size of shared memory allocated dynamically at kernel launch.

Syntax (predefined)

.sreg .u32 %dynamic_smem_size;

Description

Size of shared memory allocated dynamically at kernel launch.

A predefined, read-only special register initialized with size of shared memory allocated dynamically for the CTA of a kernel at launch time.

PTX ISA Notes

Introduced in PTX ISA version 4.1.

Target ISA Notes

Requires sm_20 or higher.

Examples

    mov.u32  %r, %dynamic_smem_size;

11. Directives

11.1. PTX Module Directives

The following directives declare the PTX ISA version of the code in the module, the target architecture for which the code was generated, and the size of addresses within the PTX module.
  • .version
  • .target
  • .address_size

11.1.1. PTX Module Directives: .version

.version

PTX ISA version number.

Syntax

.version  major.minor    // major, minor are integers

Description

Specifies the PTX language version number.

The major number is incremented when there are incompatible changes to the PTX language, such as changes to the syntax or semantics. The version major number is used by the PTX compiler to ensure correct execution of legacy PTX code.

The minor number is incremented when new features are added to PTX.

Semantics

Indicates that this module must be compiled with tools that support an equal or greater version number.

Each PTX module must begin with a .version directive, and no other .version directive is allowed anywhere else within the module.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples

    .version 3.1
    .version 3.0
    .version 2.3

11.1.2. PTX Module Directives: .target

.target

Architecture and Platform target.

Syntax

.target stringlist         // comma separated list of target specifiers
string = { sm_70,                       // sm_7x target architectures
           sm_60, sm_61, sm_62,         // sm_6x target architectures

           sm_50, sm_52, sm_53,         // sm_5x target architectures
           sm_30, sm_32, sm_35, sm_37   // sm_3x target architectures
           sm_20,                       // sm_2x target architectures
           sm_10, sm_11, sm_12, sm_13,  // sm_1x target architectures
           texmode_unified, texmode_independent,   // texturing mode
           debug,                                  // platform option
           map_f64_to_f32 };                       // platform option

Description

Specifies the set of features in the target architecture for which the current PTX code was generated. In general, generations of SM architectures follow an onion layer model, where each generation adds new features and retains all features of previous generations. Therefore, PTX code generated for a given target can be run on later generation devices.

Semantics

Each PTX module must begin with a .version directive, immediately followed by a .target directive containing a target architecture and optional platform options. A .target directive specifies a single target architecture, but subsequent .target directives can be used to change the set of target features allowed during parsing. A program with multiple .target directives will compile and run only on devices that support all features of the highest-numbered architecture listed in the program.

PTX features are checked against the specified target architecture, and an error is generated if an unsupported feature is used.  The following table summarizes the features in PTX that vary according to target architecture.

Target Description
sm_70 Baseline feature set for sm_70 architecture.
Target Description
sm_60 Baseline feature set for sm_60 architecture.
sm_61 Baseline feature set for sm_60 architecture.
sm_62 Baseline feature set for sm_60 architecture.
Target Description
sm_50 Baseline feature set for sm_50 architecture.
sm_52 Baseline feature set for sm_50 architecture.
sm_53 Adds support for arithmetic, comparsion and texture instructions for .f16 and .f16x2 types.
Target Description
sm_30 Baseline feature set for sm_30 architecture.
sm_32

Adds 64-bit {atom,red}.{and,or,xor,min,max} instructions.

Adds shf instruction.

Adds ld.global.nc instruction.
sm_35

Adds support for CUDA Dynamic Parallelism.
sm_37

Baseline feature set for sm_35 architecture.

Target Description
sm_20 Baseline feature set for sm_20 architecture.

Target Description
sm_10

Baseline feature set for sm_10 architecture.

Requires map_f64_to_f32 if any .f64 instructions used.
sm_11

Adds 64-bit {atom,red}.{and,or,xor,min,max} instructions.

Requires map_f64_to_f32 if any .f64 instructions used.
sm_12

Adds {atom,red}.shared, 64-bit {atom,red}.global, vote instructions.

Requires map_f64_to_f32 if any .f64 instructions used.
sm_13

Adds double-precision support, including expanded rounding modifiers.

Disallows use of map_f64_to_f32.

The texturing mode is specified for an entire module and cannot be changed within the module.

The .target debug option declares that the PTX file contains DWARF debug information, and subsequent compilation of PTX will retain information needed for source-level debugging. If the debug option is declared, an error message is generated if no DWARF information is found in the file. The debug option requires PTX ISA version 3.0 or later.

map_f64_to_f32 indicates that all double-precision instructions map to single-precision regardless of the target architecture. This enables high-level language compilers to compile programs containing type double to target device that do not support double-precision operations. Note that .f64 storage remains as 64-bits, with only half being used by instructions converted from .f64 to .f32.

Notes

Targets of the form compute_xx are also accepted as synonyms for sm_xx targets.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target strings sm_10 and sm_11 introduced in PTX ISA version 1.0.

Target strings sm_12 and sm_13 introduced in PTX ISA version 1.2.

Target string sm_20 introduced in PTX ISA version 2.0.

Target string sm_30 introduced in PTX ISA version 3.0.

Target string sm_35 introduced in PTX ISA version 3.1.

Target strings sm_32 and sm_50 introduced in PTX ISA version 4.0.

Target strings sm_37 and sm_52 introduced in PTX ISA version 4.1.

Target string sm_53 introduced in PTX ISA version 4.2.

Target string sm_60, sm_61, sm_62 introduced in PTX ISA version 5.0.

Target string sm_70 introduced in PTX ISA version 6.0.

Texturing mode introduced in PTX ISA version 1.5.

Platform option debug introduced in PTX ISA version 3.0.

Target ISA Notes

The .target directive is supported on all target architectures.

Examples

    .target sm_10       // baseline target architecture
    .target sm_13       // supports double-precision
    .target sm_20, texmode_independent

11.1.3. PTX Module Directives: .address_size

.address_size

Address size used throughout PTX module.

Syntax

.address_size  address-size
address-size = { 32, 64 };

Description

Specifies the address size assumed throughout the module by the PTX code and the binary DWARF information in PTX.

Redefinition of this directive within a module is not allowed. In the presence of separate compilation all modules must specify (or default to) the same address size.

The .address_size directive is optional, but it must immediately follow the .targetdirective if present within a module.

Semantics

If the .address_size directive is omitted, the address size defaults to 32.

PTX ISA Notes

Introduced in PTX ISA version 2.3.

Target ISA Notes

Supported on all target architectures.

Examples

// example directives
   .address_size 32       // addresses are 32 bit
   .address_size 64       // addresses are 64 bit

// example of directive placement within a module
   .version 2.3
   .target sm_20
   .address_size 64
...
.entry foo () {
...
}

11.2. Specifying Kernel Entry Points and Functions

The following directives specify kernel entry points and functions.
  • .entry
  • .func

11.2.1. Kernel and Function Directives: .entry

.entry

Kernel entry point and body, with optional parameters.

Syntax

.entry kernel-name ( param-list )  kernel-body
.entry kernel-name  kernel-body

Description

Defines a kernel entry point name, parameters, and body for the kernel function.

Parameters are passed via .param space memory and are listed within an optional parenthesized parameter list. Parameters may be referenced by name within the kernel body and loaded into registers using ld.param instructions.

In addition to normal parameters, opaque .texref, .samplerref, and .surfref variables may be passed as parameters. These parameters can only be referenced by name within texture and surface load, store, and query instructions and cannot be accessed via ld.param instructions.

The shape and size of the CTA executing the kernel are available in special registers.

Semantics

Specify the entry point for a kernel program.

At kernel launch, the kernel dimensions and properties are established and made available via special registers, e.g., %ntid, %nctaid, etc.

PTX ISA Notes

For PTX ISA version 1.4 and later, parameter variables are declared in the kernel parameter list. For PTX ISA versions 1.0 through 1.3, parameter variables are declared in the kernel body.

The maximum memory size supported by PTX for normal (non-opaque type) parameters is 4352 bytes. Prior to PTX ISA version 1.5, the maximum size was 256 bytes. The CUDA and OpenCL drivers support the following limits for parameter memory:

Driver Parameter memory size
CUDA 256 bytes for sm_1x, 4096 bytes for sm_2x and higher
OpenCL 4352 bytes for all targets

Target ISA Notes

Supported on all target architectures.

Examples

.entry cta_fft
.entry filter ( .param .b32 x, .param .b32 y, .param .b32 z )
{
    .reg .b32 %r<99>;
    ld.param.b32  %r1, [x];
    ld.param.b32  %r2, [y];
    ld.param.b32  %r3, [z];
    ...
}

11.2.2. Kernel and Function Directives: .func

.func

Function definition.

Syntax

.func fname function-body
.func fname (param-list) function-body
.func (ret-param) fname (param-list) function-body

Description

Defines a function, including input and return parameters and optional function body.

A .func definition with no body provides a function prototype.

The parameter lists define locally-scoped variables in the function body. Parameters must be base types in either the register or parameter state space. Parameters in register state space may be referenced directly within instructions in the function body. Parameters in .param space are accessed using ld.param and st.param instructions in the body. Parameter passing is call-by-value.

The last parameter in the parameter list may be a .param array of type .b8 with no size specified. It is used to pass an arbitrary number of parameters to the function packed into a single array object.

When calling a function with such an unsized last argument, the last argument may be omitted from the call instruction if no parameter is passed through it. Accesses to this array parameter must be within the bounds of the array. The result of an access is undefined if no array was passed, or if the access was outside the bounds of the actual array being passed.

Semantics

The PTX syntax hides all details of the underlying calling convention and ABI.

The implementation of parameter passing is left to the optimizing translator, which may use a combination of registers and stack locations to pass parameters.

Release Notes

For PTX ISA version 1.x code, parameters must be in the register state space, there is no stack, and recursion is illegal.

PTX ISA versions 2.0 and later with target sm_20 or higher allow parameters in the .param state space, implements an ABI with stack, and supports recursion.

PTX ISA versions 2.0 and later with target sm_20 or higher support at most one return value.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Support for unsized array parameter introduced in PTX ISA version 6.0.

Target ISA Notes

Functions without unsized array parameter supported on all target architectures.

Unsized array parameter requires sm_30 or higher.

Examples

    .func (.reg .b32 rval) foo (.reg .b32 N, .reg .f64 dbl) 
    {
    .reg .b32 localVar;

    ... use N, dbl;
    other code;

    mov.b32 rval,result;
    ret;
    }

    ...
    call (fooval), foo, (val0, val1);  // return value in fooval
    ...

    .func (.param .u32 rval) bar(.param .u32 N, .param .align 4 .b8 numbers[])
    {
        .reg .b32 input0, input1;
        ld.param.b32   input0, [numbers + 0];
        ld.param.b32   input1, [numbers + 4];
        …
        other code;
        ret;
    }
    ...

    .param .u32 N;
    .param .align 4 .b8 numbers[8];
    st.param.u32    [N], 2;
    st.param.b32    [numbers + 0], 5;
    st.param.b32    [numbers + 4], 10;
    call (rval), bar, (N, numbers);
    ...

11.3. Control Flow Directives

PTX provides directives for specifying potential targets for indirect branch and call instructions. See the descriptions of bra and call for more information.
  • .branchtargets
  • .calltargets
  • .callprototype

11.3.1. Control Flow Directives: .branchtargets

.branchtargets

Declare a list of potential branch targets.

Syntax

Label:   .branchtargets  list-of-labels ;

Description

Declares a list of potential branch targets for a subsequent indirect branch, and assocates the list with the label at the start of the line.

All control flow labels in the list must occur within the same function as the declaration.

The list of labels may use the compact, shorthand syntax for enumerating a range of labels having a common prefix.

PTX ISA Notes

Introduced in PTX ISA version 2.1.

Note: Indirect branch is currently unimplemented.

Target ISA Notes

Requires sm_20 or higher.

Examples

// includes Lbl0, ..., Lbl9
Tgtlist:  .branchtargets  Loop, Lbl<10>, Done;
...
@p   bra  %r1, Tgtlist;
...

11.3.2. Control Flow Directives: .calltargets

.calltargets

Declare a list of potential call targets.

Syntax

Label:   .calltargets  list-of-functions ;

Description

Declares a list of potential call targets for a subsequent indirect call, and assocates the list with the label at the start of the line.

All functions named in the list must be declared prior to the .calltargets directive, and all functions must have the same type signature.

PTX ISA Notes

Introduced in PTX ISA version 2.1.

Target ISA Notes

Requires sm_20 or higher.

Examples

calltgt:  .calltargets  fastsin, fastcos;
...
@p   call  (%f1), %r0, (%x), calltgt;
...

11.3.3. Control Flow Directives: .callprototype

.callprototype

Declare a prototype for use in an indirect call.

Syntax

label: .callprototype _ ;              // no input or return parameters
label: .callprototype _ (param-list);  // input params,
                                       // no return params
label: .callprototype (ret-param) _ ;  // no input params,
                                       // return params
label: .callprototype (ret-param) _ (param-list);  // input, return
                                       // parameters

Description

Defines a prototype with no specific function name, and associates the prototype with a label. The prototype may then be used in indirect call instructions where there is incomplete knowledge of the possible call targets.

Parameters may have either base types in the register or parameter state spaces, or array types in parameter state space. The sink symbol '_' may be used to avoid dummy parameter names.

PTX ISA Notes

Introduced in PTX ISA version 2.1.

Target ISA Notes

Requires sm_20 or higher.

Examples

Fproto1: .callprototype  _ ;
Fproto2: .callprototype  _ (.param .f32 _);
Fproto3: .callprototype  (.param .u32 _) _ ;
Fproto4: .callprototype  (.param .u32 _) _ (.param .f32 _);
...
@p   call  (%val), %r0, (%f1), Fproto4;
...

// example of array parameter
Fproto5: .callprototype _ (.param .b8 _[12]);

11.4. Performance-Tuning Directives

To provide a mechanism for low-level performance tuning, PTX supports the following directives, which pass information to the backend optimizing compiler.

  • .maxnreg
  • .maxntid
  • .reqntid
  • .minnctapersm
  • .maxnctapersm (deprecated)
  • .pragma

The .maxnreg directive specifies the maximum number of registers to be allocated to a single thread; the .maxntid directive specifies the maximum number of threads in a thread block (CTA); the .reqntid directive specifies the required number of threads in a thread block (CTA); and the .minnctapersm directive specifies a minimum number of thread blocks to be scheduled on a single multiprocessor (SM). These can be used, for example, to throttle the resource requirements (e.g., registers) to increase total thread count and provide a greater opportunity to hide memory latency. The .minnctapersm directive can be used together with either the .maxntid or .reqntid directive to trade-off registers-per-thread against multiprocessor utilization without needed to directly specify a maximum number of registers. This may achieve better performance when compiling PTX for multiple devices having different numbers of registers per SM.

Currently, the .maxnreg, .maxntid, .reqntid, and .minnctapersm directives may be applied per-entry and must appear between an .entry directive and its body. The directives take precedence over any module-level constraints passed to the optimizing backend. A warning message is generated if the directives' constraints are inconsistent or cannot be met for the specified target device.

A general .pragma directive is supported for passing information to the PTX backend. The directive passes a list of strings to the backend, and the strings have no semantics within the PTX virtual machine model. The interpretation of .pragma values is determined by the backend implementation and is beyond the scope of the PTX ISA. Note that .pragma directives may appear at module (file) scope, at entry-scope, or as statements within a kernel or device function body.

11.4.1. Performance-Tuning Directives: .maxnreg

.maxnreg

Maximum number of registers that can be allocated per thread.

Syntax

.maxnreg n

Description

Declare the maximum number of registers per thread in a CTA.

Semantics

The compiler guarantees that this limit will not be exceeded. The actual number of registers used may be less; for example, the backend may be able to compile to fewer registers, or the maximum number of registers may be further constrained by .maxntid and .maxctapersm.

PTX ISA Notes

Introduced in PTX ISA version 1.3.

Target ISA Notes

Supported on all target architectures.

Examples

    .entry foo .maxnreg 16 { ... }  // max regs per thread = 16

11.4.2. Performance-Tuning Directives: .maxntid

.maxntid

Maximum number of threads in the thread block (CTA).

Syntax

.maxntid nx
.maxntid nx, ny
.maxntid nx, ny, nz

Description

Declare the maximum number of threads in the thread block (CTA). This maximum is specified by giving the maximum extent of each dimension of the 1D, 2D, or 3D CTA.  The maximum number of threads is the product of the maximum extent in each dimension.

Semantics

The maximum number of threads in the thread block, computed as the product of the maximum extent specified for each dimension, is guaranteed not to be exceeded in any invocation of the kernel in which this directive appears. Exceeding the maximum number of threads results in a runtime error or kernel launch failure.

Note that this directive guarantees that the total number of threads does not exceed the maximum, but does not guarantee that the limit in any particular dimension is not exceeded.

PTX ISA Notes

Introduced in PTX ISA version 1.3.

Target ISA Notes

Supported on all target architectures.

Examples

    .entry foo .maxntid 256       { ... }  // max threads = 256
    .entry bar .maxntid 16,16,4   { ... }  // max threads = 1024

11.4.3. Performance-Tuning Directives: .reqntid

.reqntid

Number of threads in the thread block (CTA).

Syntax

.reqntid nx
.reqntid nx, ny
.reqntid nx, ny, nz

Description

Declare the number of threads in the thread block (CTA) by specifying the extent of each dimension of the 1D, 2D, or 3D CTA. The total number of threads is the product of the number of threads in each dimension.

Semantics

The size of each CTA dimension specified in any invocation of the kernel is required to be equal to that specified in this directive. Specifying a different CTA dimension at launch will result in a runtime error or kernel launch failure.

Notes

The .reqntid directive cannot be used in conjunction with the .maxntid directive.

PTX ISA Notes

Introduced in PTX ISA version 2.1.

Target ISA Notes

Supported on all target architectures.

Examples

    .entry foo .reqntid 256       { ... }  // num threads = 256
    .entry bar .reqntid 16,16,4   { ... }  // num threads = 1024

11.4.4. Performance-Tuning Directives: .minnctapersm

.minnctapersm

Minimum number of CTAs per SM.

Syntax

.minnctapersm ncta

Description

Declare the minimum number of CTAs from the kernel's grid to be mapped to a single multiprocessor (SM).

Notes

Optimizations based on .minnctapersm need either .maxntid or .reqntid to be specified as well. In PTX ISA version 2.1 or higher, a warning is generated if .minnctapersm is specified without specifying either .maxntid or .reqntid.

PTX ISA Notes

Introduced in PTX ISA version 2.0 as a replacement for .maxnctapersm.

Target ISA Notes

Supported on all target architectures.

Examples

    .entry foo .maxntid 256 .minnctapersm 4 { ... }

11.4.5. Performance-Tuning Directives: .maxnctapersm (deprecated)

.maxnctapersm

Maximum number of CTAs per SM.

Syntax

.maxnctapersm ncta

Description

Declare the maximum number of CTAs from the kernel's grid that may be mapped to a single multiprocessor (SM).

Notes

Optimizations based on .maxnctapersm generally need .maxntid to be specified as well. The optimizing backend compiler uses .maxntid and .maxnctapersm to compute an upper-bound on per-thread register usage so that the specified number of CTAs can be mapped to a single multiprocessor. However, if the number of registers used by the backend is sufficiently lower than this bound, additional CTAs may be mapped to a single multiprocessor. For this reason, .maxnctapersm has been renamed to .minnctapersm in PTX ISA version 2.0.

PTX ISA Notes

Introduced in PTX ISA version 1.3. Deprecated in PTX ISA version 2.0.

Target ISA Notes

Supported on all target architectures.

Examples

    .entry foo .maxntid 256 .maxnctapersm 4 { ... }

11.4.6. Performance-Tuning Directives: .pragma

.pragma

Pass directives to PTX backend compiler.

Syntax

.pragma list-of-strings ;

Description

Pass module-scoped, entry-scoped, or statement-level directives to the PTX backend compiler.

The .pragma directive may occur at module-scope, at entry-scope, or at statement-level.

Semantics

The interpretation of .pragma directive strings is implementation-specific and has no impact on PTX semantics. See Descriptions of .pragma Strings for descriptions of the pragma strings defined in ptxas.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

Supported on all target architectures.

Examples

    .pragma "nounroll";    // disable unrolling in backend

    // disable unrolling for current kernel
    .entry foo .pragma "nounroll"; { ... }

11.5. Debugging Directives

DWARF-format debug information is passed through PTX modules using the following directives:

  • @@DWARF
  • .section
  • .file
  • .loc

The .section directive was introduced in PTX ISA version 2.0 and replaces the @@DWARF syntax. The @@DWARF syntax was deprecated in PTX ISA version 2.0 but is supported for legacy PTX ISA version 1.x code.

Beginning with PTX ISA version 3.0, PTX files containing DWARF debug information should include the .target debug platform option. This forward declaration directs PTX compilation to retain mappings for source-level debugging.

11.5.1. Debugging Directives: @@dwarf

@@dwarf

DWARF-format information.

Syntax

@@DWARF dwarf-string

dwarf-string may have one of the 
.byte   byte-list   // comma-separated hexadecimal byte values
.4byte  int32-list  // comma-separated hexadecimal integers in range [0..232-1]
.quad   int64-list  // comma-separated hexadecimal integers in range [0..264-1]
.4byte  label
.quad   label

PTX ISA Notes

Introduced in PTX ISA version 1.2. Deprecated as of PTX ISA version 2.0, replaced by .section directive.

Target ISA Notes

Supported on all target architectures.

Examples

@@DWARF .section .debug_pubnames, "", @progbits
@@DWARF .byte   0x2b, 0x00, 0x00, 0x00, 0x02, 0x00
@@DWARF .4byte  .debug_info
@@DWARF .4byte  0x000006b5, 0x00000364, 0x61395a5f, 0x5f736f63
@@DWARF .4byte  0x6e69616d, 0x63613031, 0x6150736f, 0x736d6172
@@DWARF .byte   0x00, 0x00, 0x00, 0x00, 0x00

11.5.2. Debugging Directives: .section

.section

PTX section definition.

Syntax

.section section_name { dwarf-lines }

dwarf-lines have the following formats:
  .b8    byte-list   // comma-separated list of integers
                     // in range [0..255]
  .b16   int16-list  // comma-separated list of integers
                     // in range [0..216-1]
  .b32   int32-list  // comma-separated list of integers
                     // in range [0..232-1]
  .b64   int64-list  // comma-separated list of integers
                     // in range [0..264-1]
  .b32   label
  .b64   label
  .b32   label+imm   // a sum of label address plus a constant integer byte                            
                     // offset(signed, 32bit)
  .b64   label+imm   // a sum of label address plus a constant integer byte                            
                     // offset(signed, 64bit)

PTX ISA Notes

Introduced in PTX ISA version 2.0, replaces @@DWARF syntax.

label+imm expression introduced in PTX ISA version 3.2.

Support for .b16 integers in dwarf-lines introduced in PTX ISA version 6.0.

Target ISA Notes

Supported on all target architectures.

Examples

.section .debug_pubnames
{
    .b8     0x2b, 0x00, 0x00, 0x00, 0x02, 0x00
    .b32    .debug_info
    .b32    0x000006b5, 0x00000364, 0x61395a5f, 0x5f736f63
    .b32    0x6e69616d, 0x63613031, 0x6150736f, 0x736d6172
    .b8     0x00, 0x00, 0x00, 0x00, 0x00
}

.section .debug_info
{
    .b32 11430           
    .b8 2, 0  
    .b32 .debug_abbrev
    .b8 8, 1, 108, 103, 101, 110, 102, 101, 58, 32, 69, 68, 71, 32, 52, 46, 49
    .b8 0            
    .b32 3, 37, 176
    .b32 .debug_loc+0x4              
    .b8 11, 112, 97
}

11.5.3. Debugging Directives: .file

.file

Source file name.

Syntax

.file file_index "filename" {, timestamp, file_size}

Description

Associates a source filename with an integer index. .loc directives reference source files by index.

.file directive allows optionally specifying an unsigned number representing time of last modification and an unsigned integer representing size in bytes of source file. timestamp and file_size value can be 0 to indicate this information is not available.

timestamp value is in format of C and C++ data type time_t.

file_size is an unsigned 64-bit integer.

The .file directive is allowed only in the outermost scope, i.e., at the same level as kernel and device function declarations.

Semantics

If timestamp and file size are not specified, they default to 0.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Timestamp and file size introduced in PTX ISA version 3.2.

Target ISA Notes

Supported on all target architectures.

Examples

.file 1 "example.cu"
.file 2 "kernel.cu"
.file 1 “kernel.cu”, 1339013327, 64118

11.5.4. Debugging Directives: .loc

.loc

Source file location.

Syntax

.loc file_index line_number column_position

Description

Declares the source file location (source file, line number, and column position) to be associated with lexically subsequent PTX instructions. .loc refers to file_index which is defined by a .file directive. Note that a PTX instruction may have a single associated source location, determined by the nearest lexically preceding .loc directive, or no associated source location if there is no preceding .loc directive. Labels in PTX inherit the location of the closest lexically following instruction. A label with no following PTX instruction has no associated source location.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples

    .loc 2 4237 0
L1:                        // line 4237, col 0 of file #2,
                           // inherited from mov
    mov.u32  %r1,%r2;      // line 4237, col 0 of file #2
    add.u32  %r2,%r1,%r3;  // line 4237, col 0 of file #2
...
L2:                        // line 4239, col 5 of file #2,
                           // inherited from sub
    .loc 2 4239 5
    sub.u32  %r2,%r1,%r3;  // line 4239, col 5 of file #2

11.6. Linking Directives

  • .extern
  • .visible
  • .weak

11.6.1. Linking Directives: .extern

.extern

External symbol declaration.

Syntax

.extern identifier

Description

Declares identifier to be defined external to the current module. The identifier must be declared .visible in the module where it is defined.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples

.extern .global .b32 foo;  // foo is defined in another module

11.6.2. Linking Directives: .visible

.visible

Visible (externally) symbol declaration.

Syntax

.visible identifier

Description

Declares identifier to be globally visible. Unlike C, where identifiers are globally visible unless declared static, PTX identifiers are visible only within the current module unless declared .visible outside the current.

PTX ISA Notes

Introduced in PTX ISA version 1.0.

Target ISA Notes

Supported on all target architectures.

Examples

.visible .global .b32 foo;  // foo will be externally visible

11.6.3. Linking Directives: .weak

.weak

Visible (externally) symbol declaration.

Syntax

.weak identifier

Description

Declares identifier to be globally visible but weak. Weak symbols are similar to globally vsible symbols, except during linking, weak symbols are only chosen after global and local symbols during symbol resolution. Unlike globally visible symbols, multiple object files may declare the same weak symbol, and references to a symbol get resolved against a weak symbol only if no global or local symbols have the same name.

PTX ISA Notes

Introduced in PTX ISA version 3.1.

Target ISA Notes

Supported on all target architectures.

Examples

.weak .func (.reg .b32 val) foo;  // foo will be externally visible

11.6.4. Linking Directives: .common

.common

Visible (externally) symbol declaration.

Syntax

.common identifier

Description

Declares identifier to be globally visible but “common”.

Common symbols are similar to globally visible symbols. However multiple object files may declare the same common symbol and they may have different types and sizes and references to a symbol get resolved against a common symbol with the largest size.

Only one object file can initialize a common symbol and that must have the largest size among all other definitions of that common symbol from different object files.

.common linking directive can be used only on variables with .global storage. It cannot be used on function symbols or on symbols with opaque type.

PTX ISA Notes

Introduced in PTX ISA version 5.0.

Target ISA Notes

.common directive requires sm_20 or higher.

Examples

.common .global .u32 gbl;

12. Release Notes

This section describes the history of change in the PTX ISA and implementation. The first section describes ISA and implementation changes in the current release of PTX ISA version 6.0, and the remaining sections provide a record of changes in previous releases of PTX ISA versions back to PTX ISA version 2.0.

Table 30 shows the PTX release history.

Table 30. PTX Release History
PTX ISA Version CUDA Release Supported Targets
PTX ISA 1.0 CUDA 1.0 sm_{10,11}
PTX ISA 1.1 CUDA 1.1 sm_{10,11}
PTX ISA 1.2 CUDA 2.0 sm_{10,11,12,13}
PTX ISA 1.3 CUDA 2.1 sm_{10,11,12,13}
PTX ISA 1.4 CUDA 2.2 sm_{10,11,12,13}
PTX ISA 1.5 driver r190 sm_{10,11,12,13}
PTX ISA 2.0 CUDA 3.0, driver r195 sm_{10,11,12,13}, sm_20
PTX ISA 2.1 CUDA 3.1, driver r256 sm_{10,11,12,13}, sm_20
PTX ISA 2.2 CUDA 3.2, driver r260 sm_{10,11,12,13}, sm_20
PTX ISA 2.3 CUDA 4.0, driver r270 sm_{10,11,12,13}, sm_20
PTX ISA 3.0 CUDA 4.2, driver r295 sm_{10,11,12,13}, sm_20
CUDA 4.1, driver r285 sm_{10,11,12,13}, sm_20, sm_30
PTX ISA 3.1 CUDA 5.0, driver r302 sm_{10,11,12,13}, sm_20, sm_{30,35}
PTX ISA 3.2 CUDA 5.5, driver r319 sm_{10,11,12,13}, sm_20, sm_{30,35}
PTX ISA 4.0 CUDA 6.0, driver r331 sm_{10,11,12,13}, sm_20, sm_{30,32,35} , sm_50
PTX ISA 4.1 CUDA 6.5, driver r340 sm_{10,11,12,13}, sm_20, sm_{30,32,35,37} , sm_{50,52}
PTX ISA 4.2 CUDA 7.0, driver r346 sm_{10,11,12,13}, sm_20, sm_{30,32,35,37} , sm_{50,52,53}
PTX ISA 4.3 CUDA 7.5, driver r352 sm_{10,11,12,13}, sm_20, sm_{30,32,35,37} , sm_{50,52,53}
PTX ISA 5.0 CUDA 8.0, driver r361 sm_{10,11,12,13}, sm_20, sm_{30,32,35,37} , sm_{50,52,53} , sm_{60,61,62}
PTX ISA 6.0 CUDA 9.0, driver r384 sm_{10,11,12,13}, sm_20, sm_{30,32,35,37} , sm_{50,52,53} , sm_{60,61,62}, sm_70

12.1. Changes in PTX ISA Version 6.0

New Features

PTX ISA version 6.0 introduces the following new features:
  • Support for sm_70 target architecture.
  • Specifies the memory consistency model for programs running on sm_70 and later architectures.
  • Various extensions to memory instructions to specify memory synchronization semantics and scopes at which such synchronization can be observed.
  • New instruction wmma for matrix operations which allows loading matrices from memory, performing multiply-and-accumulate on them and storing result in memory.
  • Support for new barrier instruction.
  • Extends neg instruction to support .f16 and .f16x2 types.
  • A new instruction fns which allows finding n-th set bit in integer.
  • A new instruction bar.warp.sync which allows synchronizing threads in warp.
  • Extends vote and shfl instructions with .sync modifier which waits for specified threads before executing the vote and shfl operation respectively.
  • A new instruction match.sync which allows broadcasting and comparing a value across threads in warp.
  • A new instruction brx.idx which allows branching to a label indexed from list of potential targets.
  • Support for unsized array parameter for .func which can be used to implement variadic functions.
  • Support for .b16 integer type in dwarf-lines.
  • Support for taking address of device function return parameters using mov instruction.

Semantic Changes and Clarifications

  • Semantics of bar instruction were updated to indicate that executing thread waits for other non-exited threads from it's warp.
  • Support for indirect branch introduced in PTX 2.1 which was unimplemented has been removed from the spec.
  • Support for taking address of labels, using labels in initializers which was unimplemented has been removed from the spec.
  • Support for variadic functions which was unimplemented has been removed from the spec.

Features Unimplemented in PTX ISA Version 6.0

The following features remain unimplemented in PTX ISA version 6.0:

  • Allocation of per-thread, stack-based memory using alloca.

12.2. Changes in PTX ISA Version 5.0

New Features

PTX ISA version 5.0 introduces the following new features:
  • Support for sm_60, sm_61, sm_62 target architecture.
  • Extends atomic and reduction instructions to perform fp64 add operation.
  • Extends atomic and reduction instructions to specify scope modifier.
  • A new .common directive to permit linking multiple object files containing declarations of the same symbol with different size.
  • A new dp4a instruction which allows 4-way dot product with accumulate operation.
  • A new dp2a instruction which allows 2-way dot product with accumulate operation.
  • Support for special register %clock_hi.

Semantic Changes and Clarifications

Semantics of cache modifiers on ld and st instructions were clarified to reflect cache operations are treated as performance hint only and do not change memory consistency behavior of the program.

Semantics of volatile operations on ld and st instructions were clarified to reflect how volatile operations are handled by optimizing compiler.

12.3. Changes in PTX ISA Version 4.3

New Features

PTX ISA version 4.3 introduces the following new features:
  • Support for sm_60 target architecture.
  • A new lop3 instruction which allows arbitrary logical operation on 3 inputs.
  • Adds support for 64-bit computations in extended precision arithmetic instructions.
  • Extends tex.grad instruction to support cube and acube geometries.
  • Extends tld4 instruction to support a2d, cube and acube geometries.
  • Extends tex and tld4 instructions to support optional operands for offset vector and depth compare.
  • Extends txq instruction to support querying texture fields from specific LOD.
  • Extends atomic and reduction instructions to perform fp64 add operation.

Semantic Changes and Clarifications

None.

12.4. Changes in PTX ISA Version 4.2

New Features

PTX ISA version 4.2 introduces the following new features:
  • Support for sm_53 target architecture.
  • Support for arithmetic, comparsion and texture instructions for .f16 and .f16x2 types.
  • Support for memory_layout field for surfaces and suq instruction support for querying this field.

Semantic Changes and Clarifications

Semantics for parameter passing under ABI were updated to indicate ld.param and st.param instructions used for argument passing cannot be predicated.

Semantics of {atom/red}.add.f32 were updated to indicate subnormal inputs and results are flushed to sign-preserving zero for atomic operations on global memory; whereas atomic operations on shared memory preserve subnormal inputs and results and don't flush them to zero.

12.5. Changes in PTX ISA Version 4.1

New Features

PTX ISA version 4.1 introduces the following new features:
  • Support for sm_37 and sm_52 target architectures.
  • Support for new fields array_size, num_mipmap_levels and num_samples for Textures, and the txq instruction support for querying these fields.
  • Support for new field array_size for Surfaces, and the suq instruction support for querying this field.
  • Support for special registers %total_smem_size and %dynamic_smem_size.

Semantic Changes and Clarifications

None.

12.6. Changes in PTX ISA Version 4.0

New Features

PTX ISA version 4.0 introduces the following new features:
  • Support for sm_32 and sm_50 target architectures.
  • Support for 64bit performance counter special registers %pm0_64,..,%pm7_64.
  • A new istypep instruction.
  • A new instruction, rsqrt.approx.ftz.f64 has been added to compute a fast approximation of the square root reciprocal of a value.
  • Support for a new directive .attribute for specifying special attributes of a variable.
  • Support for .managed variable attribute.

Semantic Changes and Clarifications

The vote instruction semantics were updated to clearly indicate that an inactive thread in a warp contributes a 0 for its entry when participating in vote.ballot.b32.

12.7. Changes in PTX ISA Version 3.2

New Features

PTX ISA version 3.2 introduces the following new features:
  • The texture instruction supports reads from multi-sample and multisample array textures.
  • Extends .section debugging directive to include label + immediate expressions.
  • Extends .file directive to include timestamp and file size information.

Semantic Changes and Clarifications

The vavrg2 and vavrg4 instruction semantics were updated to indicate that instruction adds 1 only if Va[i] + Vb[i] is non-negative, and that the addition result is shifted by 1 (rather than being divided by 2).

12.8. Changes in PTX ISA Version 3.1

New Features

PTX ISA version 3.1 introduces the following new features:

  • Support for sm_35 target architecture.
  • Support for CUDA Dynamic Parallelism, which enables a kernel to create and synchronize new work.
  • ld.global.nc for loading read-only global data though the non-coherent texture cache.
  • A new funnel shift instruction, shf.
  • Extends atomic and reduction instructions to perform 64-bit {and, or, xor} operations, and 64-bit integer {min, max} operations.
  • Adds support for mipmaps.
  • Adds support for indirect access to textures and surfaces.
  • Extends support for generic addressing to include the .const state space, and adds a new operator, generic(), to form a generic address for .global or .const variables used in initializers.
  • A new .weak directive to permit linking multiple object files containing declarations of the same symbol.

Semantic Changes and Clarifications

PTX 3.1 redefines the default addressing for global variables in initializers, from generic addresses to offsets in the global state space. Legacy PTX code is treated as having an implicit generic() operator for each global variable used in an initializer. PTX 3.1 code should either include explicit generic() operators in initializers, use cvta.global to form generic addresses at runtime, or load from the non-generic address using ld.global.

Instruction mad.f32 requires a rounding modifier for sm_20 and higher targets. However for PTX ISA version 3.0 and earlier, ptxas does not enforce this requirement and mad.f32 silently defaults to mad.rn.f32. For PTX ISA version 3.1, ptxas generates a warning and defaults to mad.rn.f32, and in subsequent releases ptxas will enforce the requirement for PTX ISA version 3.2 and later.

12.9. Changes in PTX ISA Version 3.0

New Features

PTX ISA version 3.0 introduces the following new features:

  • Support for sm_30 target architectures.
  • SIMD video instructions.
  • A new warp shuffle instruction.
  • Instructions mad.cc and madc for efficient, extended-precision integer multiplication.
  • Surface instructions with 3D and array geometries.
  • The texture instruction supports reads from cubemap and cubemap array textures.
  • Platform option .target debug to declare that a PTX module contains DWARF debug information.
  • pmevent.mask, for triggering multiple performance monitor events.
  • Performance monitor counter special registers %pm4..%pm7.

Semantic Changes and Clarifications

Special register %gridid has been extended from 32-bits to 64-bits.

PTX ISA version 3.0 deprecates module-scoped .reg and .local variables when compiling to the Application Binary Interface (ABI). When compiling without use of the ABI, module-scoped .reg and .local variables are supported as before. When compiling legacy PTX code (ISA versions prior to 3.0) containing module-scoped .reg or .local variables, the compiler silently disables use of the ABI.

The shfl instruction semantics were updated to clearly indicate that value of source operand a is unpredictable for inactive and predicated-off threads within the warp.

PTX modules no longer allow duplicate .version directives. This feature was unimplemented, so there is no semantic change.

Unimplemented instructions suld.p and sust.p.{u32,s32,f32} have been removed.

12.10. Changes in PTX ISA Version 2.3

New Features

PTX 2.3 adds support for texture arrays. The texture array feature supports access to an array of 1D or 2D textures, where an integer indexes into the array of textures, and then one or two single-precision floating point coordinates are used to address within the selected 1D or 2D texture.

PTX 2.3 adds a new directive, .address_size, for specifying the size of addresses.

Variables in .const and .global state spaces are initialized to zero by default.

Semantic Changes and Clarifications

The semantics of the .maxntid directive have been updated to match the current implementation. Specifically, .maxntid only guarantees that the total number of threads in a thread block does not exceed the maximum. Previously, the semantics indicated that the maximum was enforced separately in each dimension, which is not the case.

Bit field extract and insert instructions BFE and BFI now indicate that the len and pos operands are restricted to the value range 0..255.

Unimplemented instructions {atom,red}.f32.{min,max} have been removed.

12.11. Changes in PTX ISA Version 2.2

New Features

PTX 2.2 adds a new directive for specifying kernel parameter attributes; specifically, there is a new directives for specifying that a kernel parameter is a pointer, for specifying to which state space the parameter points, and for optionally specifying the alignment of the memory to which the parameter points.

PTX 2.2 adds a new field named force_unnormalized_coords to the .samplerref opaque type. This field is used in the independent texturing mode to override the normalized_coords field in the texture header. This field is needed to support languages such as OpenCL, which represent the property of normalized/unnormalized coordinates in the sampler header rather than in the texture header.

PTX 2.2 deprecates explicit constant banks and supports a large, flat address space for the .const state space. Legacy PTX that uses explicit constant banks is still supported.

PTX 2.2 adds a new tld4 instruction for loading a component (r, g, b, or a) from the four texels compising the bilinear interpolation footprint of a given texture location. This instruction may be used to compute higher-precision bilerp results in software, or for performing higher-bandwidth texture loads.

Semantic Changes and Clarifications

None.

12.12. Changes in PTX ISA Version 2.1

New Features

The underlying, stack-based ABI is supported in PTX ISA version 2.1 for sm_2x targets.

Support for indirect calls has been implemented for sm_2x targets.

New directives, .branchtargets and .calltargets, have been added for specifying potential targets for indirect branches and indirect function calls. A .callprototype directive has been added for declaring the type signatures for indirect function calls.

The names of .global and .const variables can now be specified in variable initializers to represent their addresses.

A set of thirty-two driver-specific execution environment special registers has been added. These are named %envreg0..%envreg31.

Textures and surfaces have new fields for channel data type and channel order, and the txq and suq instructions support queries for these fields.

Directive .minnctapersm has replaced the .maxnctapersm directive.

Directive .reqntid has been added to allow specification of exact CTA dimensions.

A new instruction, rcp.approx.ftz.f64, has been added to compute a fast, gross approximate reciprocal.

Semantic Changes and Clarifications

A warning is emitted if .minnctapersm is specified without also specifying .maxntid.

12.13. Changes in PTX ISA Version 2.0

New Features

Floating Point Extensions

This section describes the floating-point changes in PTX ISA version 2.0 for sm_20 targets. The goal is to achieve IEEE 754 compliance wherever possible, while maximizing backward compatibility with legacy PTX ISA version 1.x code and sm_1x targets.

The changes from PTX ISA version 1.x are as follows:

  • Single-precision instructions support subnormal numbers by default for sm_20 targets. The .ftz modifier may be used to enforce backward compatibility with sm_1x.
  • Single-precision add, sub, and mul now support .rm and .rp rounding modifiers for sm_20 targets.
  • A single-precision fused multiply-add (fma) instruction has been added, with support for IEEE 754 compliant rounding modifiers and support for subnormal numbers. The fma.f32 instruction also supports .ftz and .sat modifiers. fma.f32 requires sm_20. The mad.f32 instruction has been extended with rounding modifiers so that it's synonymous with fma.f32 for sm_20 targets. Both fma.f32 and mad.f32 require a rounding modifier for sm_20 targets.
  • The mad.f32 instruction without rounding is retained so that compilers can generate code for sm_1x targets. When code compiled for sm_1x is executed on sm_20 devices, mad.f32 maps to fma.rn.f32.
  • Single- and double-precision div, rcp, and sqrt with IEEE 754 compliant rounding have been added. These are indicated by the use of a rounding modifier and require sm_20.
  • Instructions testp and copysign have been added.

New Instructions

A load uniform instruction, ldu, has been added.

Surface instructions support additional .clamp modifiers, .clamp and .zero.

Instruction sust now supports formatted surface stores.

A count leading zeros instruction, clz, has been added.

A find leading non-sign bit instruction, bfind, has been added.

A bit reversal instruction, brev, has been added.

Bit field extract and insert instructions, bfe and bfi, have been added.

A population count instruction, popc, has been added.

A vote ballot instruction, vote.ballot.b32, has been added.

Instructions {atom,red}.add.f32 have been implemented.

Instructions {atom,red}.shared have been extended to handle 64-bit data types for sm_20 targets.

A system-level membar instruction, membar.sys, has been added.

The bar instruction has been extended as follows:

  • A bar.arrive instruction has been added.
  • Instructions bar.red.popc.u32 and bar.red.{and,or}.pred have been added.
  • bar now supports optional thread count and register operands.

Scalar video instructions (includes prmt) have been added.

Instruction isspacep for querying whether a generic address falls within a specified state space window has been added.

Instruction cvta for converting global, local, and shared addresses to generic address and vice-versa has been added.

Other New Features

Instructions ld, ldu, st, prefetch, prefetchu, isspacep, cvta, atom, and red now support generic addressing.

New special registers %nwarpid, %nsmid, %clock64, %lanemask_{eq,le,lt,ge,gt} have been added.

Cache operations have been added to instructions ld, st, suld, and sust, e.g., for prefetching to specified level of memory hierarchy. Instructions prefetch and prefetchu have also been added.

The .maxnctapersm directive was deprecated and replaced with .minnctapersm to better match its behavior and usage.

A new directive, .section, has been added to replace the @@DWARF syntax for passing DWARF-format debugging information through PTX.

A new directive, .pragma nounroll, has been added to allow users to disable loop unrolling.

Semantic Changes and Clarifications

The errata in cvt.ftz for PTX ISA versions 1.4 and earlier, where single-precision subnormal inputs and results were not flushed to zero if either source or destination type size was 64-bits, has been fixed. In PTX ISA version 1.5 and later, cvt.ftz (and cvt for .target sm_1x, where .ftz is implied) instructions flush single-precision subnormal inputs and results to sign-preserving zero for all combinations of floating-point instruction types. To maintain compatibility with legacy PTX code, if .version is 1.4 or earlier, single-precision subnormal inputs and results are flushed to sign-preserving zero only when neither source nor destination type size is 64-bits.

Components of special registers %tid, %ntid, %ctaid, and %nctaid have been extended from 16-bits to 32-bits. These registers now have type .v4.u32.

The number of samplers available in independent texturing mode was incorrectly listed as thirty-two in PTX ISA version 1.5; the correct number is sixteen.

A. Descriptions of .pragma Strings

This section describes the .pragma strings defined by ptxas.

A.1. Pragma Strings: "nounroll"

"nounroll"

Disable loop unrolling in optimizing the backend compiler.

Syntax

.pragma "nounroll";

Description

The "nounroll" pragma is a directive to disable loop unrolling in the optimizing backend compiler.

The "nounroll" pragma is allowed at module, entry-function, and statement levels, with the following meanings:

module scope
disables unrolling for all loops in module, including loops preceding the .pragma.
entry-function scope
disables unrolling for all loops in the entry function body.
statement-level pragma
disables unrolling of the loop for which the current block is the loop header.

Note that in order to have the desired effect at statement level, the "nounroll" directive must appear before any instruction statements in the loop header basic block for the desired loop. The loop header block is defined as the block that dominates all blocks in the loop body and is the target of the loop backedge. Statement-level "nounroll" directives appearing outside of loop header blocks are silently ignored.

PTX ISA Notes

Introduced in PTX ISA version 2.0.

Target ISA Notes

Requires sm_20 or higher. Ignored for sm_1x targets.

Examples

.entry foo (...)
.pragma "nounroll";  // do not unroll any loop in this function
{
...
}

.func bar (...)
{
...
L1_head:
     .pragma "nounroll";  // do not unroll this loop
     ...
@p   bra L1_end;
L1_body:
     ...
L1_continue:
     bra L1_head;
L1_end:
     ...
}

Notices

Notice

ALL NVIDIA DESIGN SPECIFICATIONS, REFERENCE BOARDS, FILES, DRAWINGS, DIAGNOSTICS, LISTS, AND OTHER DOCUMENTS (TOGETHER AND SEPARATELY, "MATERIALS") ARE BEING PROVIDED "AS IS." NVIDIA MAKES NO WARRANTIES, EXPRESSED, IMPLIED, STATUTORY, OR OTHERWISE WITH RESPECT TO THE MATERIALS, AND EXPRESSLY DISCLAIMS ALL IMPLIED WARRANTIES OF NONINFRINGEMENT, MERCHANTABILITY, AND FITNESS FOR A PARTICULAR PURPOSE.

Information furnished is believed to be accurate and reliable. However, NVIDIA Corporation assumes no responsibility for the consequences of use of such information or for any infringement of patents or other rights of third parties that may result from its use. No license is granted by implication of otherwise under any patent rights of NVIDIA Corporation. Specifications mentioned in this publication are subject to change without notice. This publication supersedes and replaces all other information previously supplied. NVIDIA Corporation products are not authorized as critical components in life support devices or systems without express written approval of NVIDIA Corporation.

Trademarks

NVIDIA and the NVIDIA logo are trademarks or registered trademarks of NVIDIA Corporation in the U.S. and other countries. Other company and product names may be trademarks of the respective companies with which they are associated.

OpenCL

OpenCL is a trademark of Apple Inc. used under license to the Khronos Group Inc.