Algorithm
Dynamic Programming
Levenshtein Distance /
Edit Distance
[Up]
Sometimes you want to determine how similar a string s is to another string t.
This is represented by the concept of Edit Distance, also called Levenshtein Distance.
The smaller the Edit Distance, the more "closer" or "similar".
The Edit Distance is the cost to change the string s to the string t by adding the following 3 operations.
Costs are ususally set for each of the 3 types of operations.
- SUBSTITUTE ... Replace one character in string s with another one. (ex.)
apble → apple
- INSERT ... Insert one character in string s.
(ex.) aple → apple
- DELETE ... delete one character in string s.
(ex.) applet → apple
To calculate the Edit Distance, we use Dynamic Programming.
In order to find the Edit Distance between strings of length $n$ and length $m$,
each element of the 2-dimensional matrix $(n+1) \times (m+1)$ is calculated,
so the computational complexty is $O(mn)$.
[Points to Understand]
Carefully check the state of the string in each cell in "Table 1: State of the string being edited".
If you understand that the state of the string consists of three elements:
- generated string
- consumed string
- cursor position (edit point)
you can easily understand the algorithm.
Example of Edit Distance Calculation
Consider an edit operation to minimize the cost of generating the string "ara" from the string "saka".
We want to reuse the reusable characters in the string "saka" while consuming other characters
to generate the string "ara" as efficiently as possible.
To solve with Dynamic Programming,
we use a table with the original (to be consumed) string in the vertical direction
and the target (to be generated) string in the horizontal direction.
Leave a blank space at the beginning of each string.
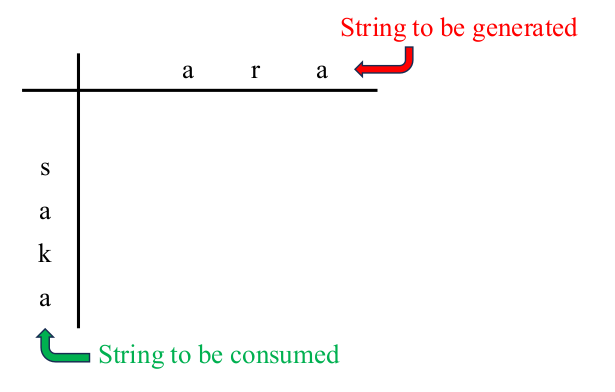
The state of the string being edited corresponding to each cell in this table is as follows.
- The position where the string is being edited is called "cursor position" or "editing point", and is represented by '|' (vertical bar).
- The characters to the left of '|' are "generated characters" in the target string.
- The caracters to the right of '|' are "characters to be consumed" in the original string.
Table 1: State of the string being edited.
| | a | r | a |
| |saka | a|saka | ar|saka | ara|saka |
| s | |aka | a|aka | ar|aka | ara|aka |
| a | |ka | a|ka | ar|ka | ara|ka |
| k | |a | a|a | ar|a | ara|a |
| a | | | a| | ar| | ara| |
If you just want to find the minimum cost, one table is fine.
If you need to record the steps of your editing operations, prepare another table.
In this example, we assume the cost of each operation as follows.
Of course you can set these values however you like.
Table 2: Costs of each Edit Operation
| Operation | Simbol | Const | Explanation |
|---|
| INSERT | $I$ | $1$ | Insert a character to the left of the cursor. |
| DELETE | $D$ | $1$ | Delete a character to the right of the cursor. |
| SUBSTITUTE | $S$ | $1$ | Substitute a character to the right of the cursor, and move the cursor position one character to the right. |
| MATCH | $M$ | $0$ | Move the cursor position one character to the right. |
In the following, the $L$ row and $R$ column elements of the table are expressed as $(L,R)$.
 |
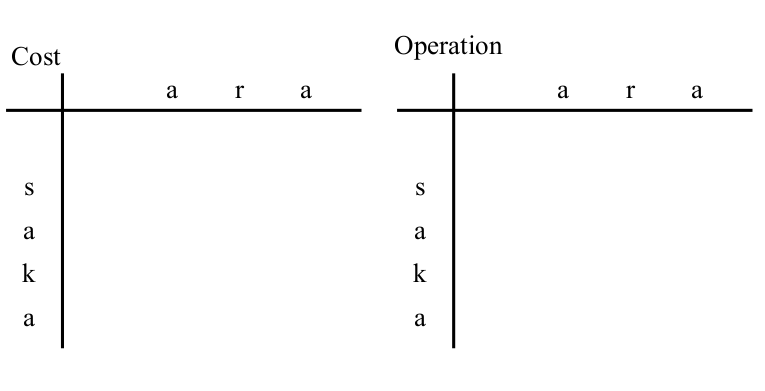Of the two tables, the left table records the minimum costs
and the right table records the last operation performed.
|
 |
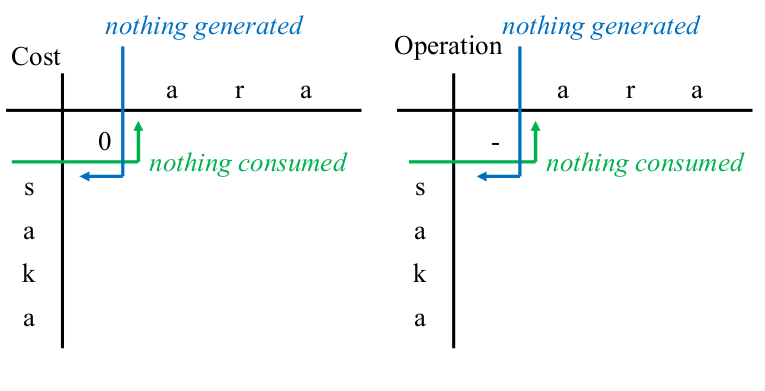Enter cost $0$ at ($0$, $0$) in the left table,
and enter '$-$' character to the ($0$, $0$) cell in the right table,
because no operation has been performed yet.
| cell | operation | String being edited |
|---|
| (0,0) | the initial state | |saka |
|
 |
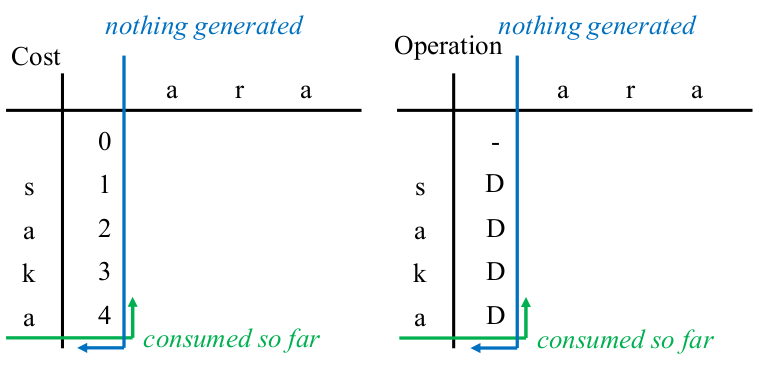Fill in the leftmost column ($L$, $0$) of the left table while adding the DELETE cost.
Since the operation is "DELETE", enter '$D$' in ($L$, $0$) cells of the right table.
| cell | operation | String being edited |
|---|
| (0,0) | initial state | |saka |
| (1,0) | DELETE 's' | |aka |
| (2,0) | DELETE 'a' | |ka |
| (3,0) | DELETE 'k' | |a |
| (4,0) | DELETE 'a' | | |
|
 |
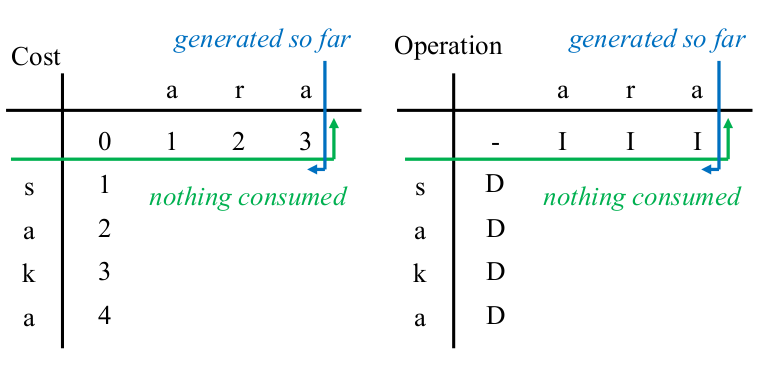Enter the cost of INSERT in the column ($0$, $R$) of the top row of the left table
while adding the INSERT cost.
Since the operation is INSERT, enter '$I$' in ($0$, $R$) in the right table.
| cell | operation | string being edited |
|---|
| (0,0) | initial state | |saka |
| (0,1) | INSERT 'a' | a|saka |
| (0,2) | INSERT 'r' | ar|saka |
| (0,3) | INSERT 'a' | ara|saka |
|
|
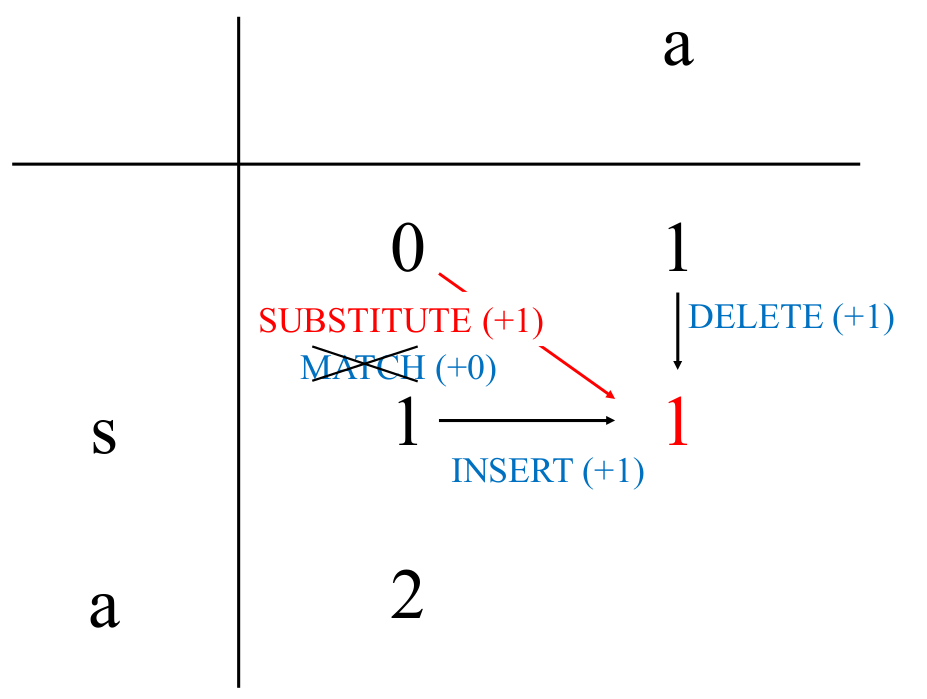
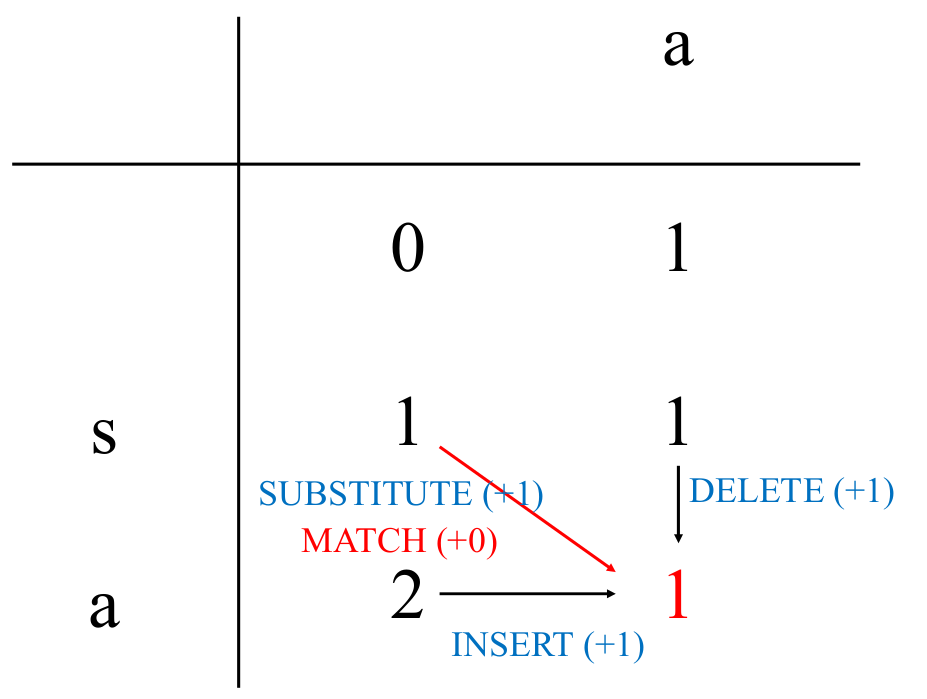
$L=1$, $R=1$.
The cost to be enterd in ($L$, $R$) in the left table is one of the following.
- SUBSTITUTE from the upper left cell ($L-1$, $R-1$)
- MATCH (= Cursor Move) from the upper left cell ($L-1$,$R-1$) $\quad$ Only when the characters are equal.
- DELETE from the upper cell ($L-1$,$R$)
- INSERT from the left cell ($L$, $R-1$)
Calculate the minimum cost and enter it in the ($L$, $R$) cell of left table,
and enter the selected operation in the ($L$, $R$) cell of the right table.
|
 |
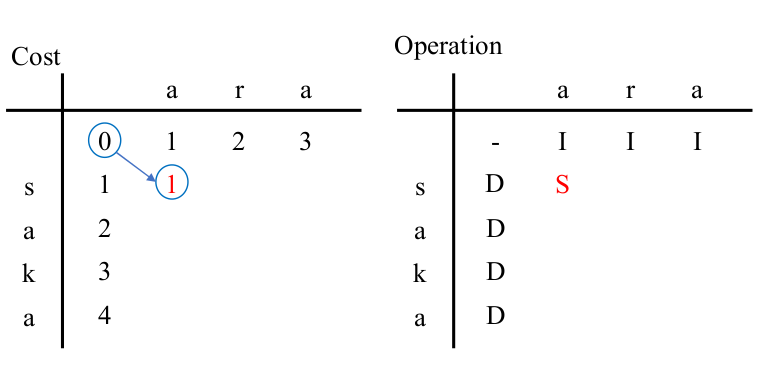Let's consider the minimum cost to reach the state ($1$, $1$) in the left table.
Since the character 's' at the cursor position is not equal to the character 'a' to be generated,
"MATCH (= Cursor Move)" can not be used.
Therefore, we consider 3 kinds of operations to arrive at ($1$, $1$):
- SUBSTITUTE 's' with 'a' from state ($0$, $0$), the cost is $0+1=1$.
- DELETE 's' from state ($0$, $1$) where 'a' was previously INSERTed, the cost is $1+1=2$.
- INSERT 'a' from state ($1$, $0$) where 's' was previously DELETEd, the cost is $1+1=2$.
Among them, "REPLACE 's' with 'a'" has the lowest cost of 1, so 1 in the left table ($1$, $1$) and '$S$' in the right table ($1$, $1$).
| cell | operation | String being edited |
|---|
| (0,0) | initial state | |saka |
| (1,1) | SUBSTITUTE 's' with 'a' | a|aka |
Regardless of the operation order, the state of ($1$, $1$) is the state where
"the leading 's' is disappeared from the string to be consumed" and
"the leading 'a' has been generated from the string to be generated".
The minimum cost to reach that state is $1$.
|
|
$L=2$, $R=1$.
The cost to be enterd in ($L$, $R$) in the left table is one of the following.
- SUBSTITUTE from the upper left cell ($L-1$, $R-1$)
- MATCH (= Cursor Move) from the upper left cell ($L-1$,$R-1$) $\quad$ Only when the characters are equal.
- DELETE from the upper cell ($L-1$,$R$)
- INSERT from the left cell ($L$, $R-1$)
Calculate the minimum cost and enter it in the ($L$, $R$) cell of left table,
and enter the selected operation in the ($L$, $R$) cell of the right table.
|
 |
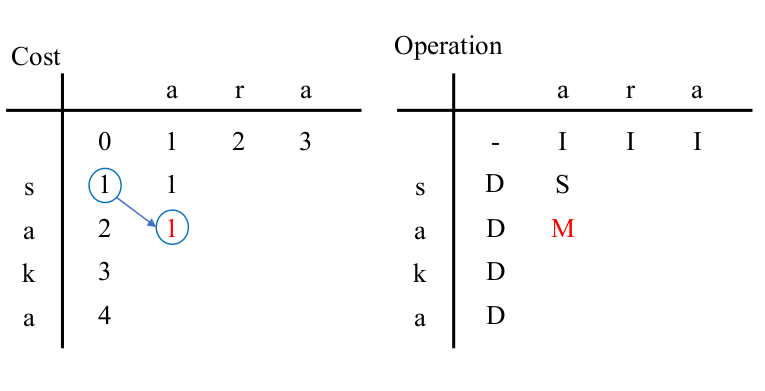In ($2$, $1$) of the left table, the character to "be consumed" and the character to "be generated" are both 'a',
so MATCH (= Cursor Move) can be used.
There are other ways to "DELETE 'a'" from ($1$, $1$) and "INSERT 'a'" from ($2$, $0$),
but "MATCH (= Cursor Move)" from ($1$, $0$) is the minimum cost.
Enter $1+0=1$ in the left table ($2$, $1$) and '$M$' in the right table ($2$, $1$).
| cell | operation | String being edited |
|---|
| (1,0) | DELETE 's' | |aka |
| (2,1) | MATCH (= Cursor Move) 'a' | a|ka |
The state of ($2$, $1$) is "First, DELETE the leading 's' from the original string,
then MOVE CURSOR through 'a' for the character of the orignal and the target is the same.
The minimum cost of the operations is $1 \mbox{(DELETE cost)} + 0 \mbox{(MATCH cost)} = 1$.
|
 |
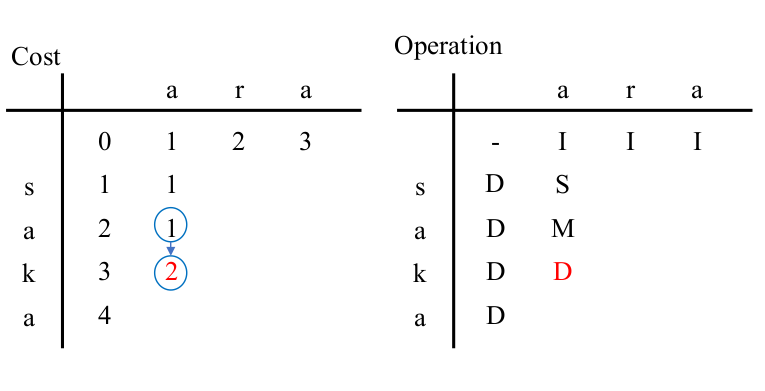In ($3$, $1$) of the left table, the character 'k' to "be consumed" is different from the character 'a' to "be generated",
so MATCH (= Cursor Move) cannot be used.
The cost of "SUBSTITUTE from ($2$, $0$)" is 3,
the cost of "INSERT from ($3$, $0$)" is 4,
and the cost of "DELETE from ($2$, $1$)" is 2.
| cell | operation | String being edited |
|---|
| (1,0) | DELETE 's' | |aka |
| (2,1) | MATCH (= Cursor Move) 'a' | a|ka |
| (3,1) | DELETE 'k' | a|a |
|
 |
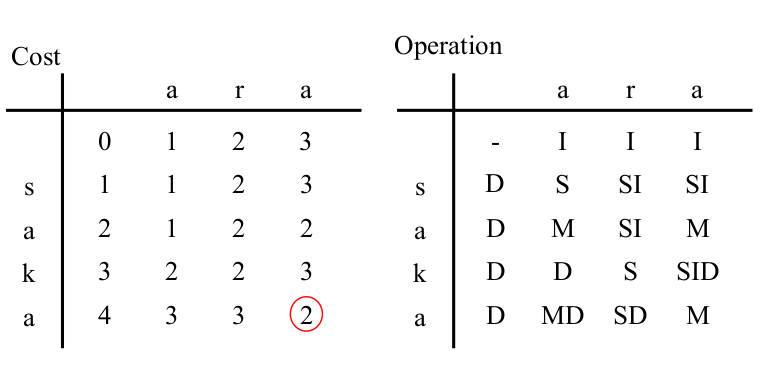All the cell is filled.
If multiple symbols are written together in the right table,
it means that either operation has the lowest cost.
For example, the symbol "SI" means "either SUBSTITUTE or INSERT is OK".
You can see that the minimum cost is $2$ by looking at the bottom right cell of the left table ($4$, $3$).
|
 |
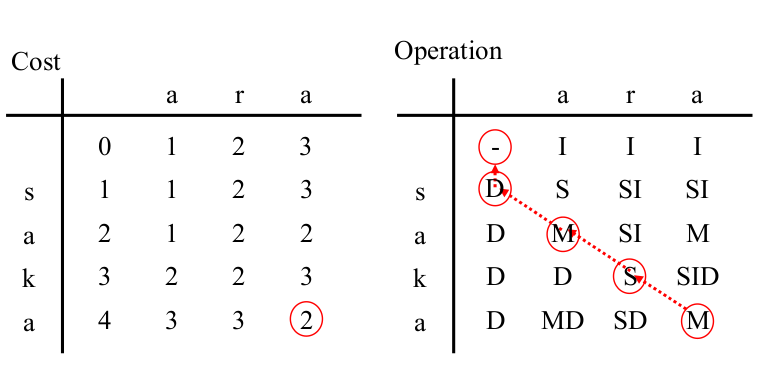You can see how to get to the minimum cost by going backwards starting from the bottom right cell of the right table.
- In case of '$S$' or '$M$', go to the upper left cell.
- In case of '$I$', go to the left cell.
- In case of '$D$', goto the upper cell.
The operation sequence with the lowest cost is as follows.
| cell/th> | operation | String being edited |
|---|
| (0,0) | initial state | |saka |
| (1,0) | DELETE 's' | |aka |
| (2,1) | MATCH 'a' | a|ka |
| (3,2) | SUBSTITUTE 'k' with'r' | ar|a |
| (4,3) | 'MATCH a' | ara| |
|
Program of Edit Distance (python, Cost only)
| EditDistance.py |
import sys
COST_DEL = 1
COST_INS = 1
COST_SUBST = 1
COST_MATCH = 0
COST = []
def solve(s,t,flag = False):
global COST
sl = len(s)
tl = len(t)
COST = [[0 for i in range(tl+1)] for j in range(sl+1)]
COST[0][0] = 0
for i in range(1,sl+1):
COST[i][0] = COST[i-1][0] + COST_DEL
for i in range(1,tl+1):
COST[0][i] = COST[0][i-1] + COST_INS
for i in range(1,sl+1):
for j in range(1,tl+1):
c_d = COST[i][j-1] + COST_DEL
c_i = COST[i-1][j] + COST_INS
c_s = COST[i-1][j-1] + COST_SUBST
if s[i-1]==t[j-1]: c_m = COST[i-1][j-1] + COST_MATCH
else: c_m = sys.maxsize
COST[i][j] = min(c_d, c_i, c_s, c_m)
return COST[sl][tl]
|
| Log of EditDistance.py |
$ python 
Python 3.9.13 (main, Aug 25 2022, 23:26:10)
[GCC 11.2.0] :: Anaconda, Inc. on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import EditDistance
>>> EditDistance.solve('saka','ara')
2
>>> print(EditDistance.COST)
[[0, 1, 2, 3], [1, 1, 2, 3], [2, 1, 2, 2], [3, 2, 2, 3], [4, 3, 3, 2]]
>>> exit()
|
Program of Edit Distance (python, Cost and Operations)
| EditDistancePath.py |
import sys
COST_DEL = 1
COST_INS = 1
COST_SUBST = 1
COST_MATCH = 0
COST = []
OP = []
def solve(s,t):
global COST, OP
sl = len(s)
tl = len(t)
COST = [[0 for i in range(tl+1)] for j in range(sl+1)]
OP = [['' for i in range(tl+1)] for j in range(sl+1)]
COST[0][0] = 0
for i in range(1,sl+1):
COST[i][0] = COST[i-1][0] + COST_DEL
OP[i][0] += 'D'
for i in range(1,tl+1):
COST[0][i] = COST[0][i-1] + COST_INS
OP[0][i] += 'I'
for i in range(1,sl+1):
for j in range(1,tl+1):
c_d = COST[i][j-1] + COST_DEL
c_i = COST[i-1][j] + COST_INS
c_s = COST[i-1][j-1] + COST_SUBST
if s[i-1]==t[j-1]: c_m = COST[i-1][j-1] + COST_MATCH
else: c_m = sys.maxsize
COST[i][j] = min(c_d, c_i, c_s, c_m)
if (c_d == COST[i][j]): OP[i][j] += 'D'
if (c_i == COST[i][j]): OP[i][j] += 'I'
if (c_s == COST[i][j]): OP[i][j] += 'S'
if (c_m == COST[i][j]): OP[i][j] += 'M'
return COST[sl][tl], getPath(s,t)
def getPath(s,t):
global OP
r = []
row = len(s)
col = len(t)
while row > 0 or col > 0:
s_ch = s[row-1]
t_ch = t[col-1]
if 'M' in OP[row][col]:
r.append('MATCH '+s_ch)
row -= 1
col -= 1
elif 'S' in OP[row][col]:
r.append('SUBSTITUTE '+s_ch+' with '+t_ch)
row -= 1
col -= 1
elif 'I' in OP[row][col]:
r.append('INSERT '+t_ch)
col -= 1
elif 'D' in OP[row][col]:
r.append('DELETE '+s_ch)
row -= 1
r.reverse()
return r
|
| Log of EditDistancePath.py |
$ python
Python 3.9.13 (main, Aug 25 2022, 23:26:10)
[GCC 11.2.0] :: Anaconda, Inc. on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import EditDistancePath
>>> EditDistancePath.solve('saka','ara')
(2, ['DELETE s', 'MATCH a', 'SUBSTITUTE k with r', 'MATCH a'])
>>> print(EditDistancePath.COST)
[[0, 1, 2, 3], [1, 1, 2, 3], [2, 1, 2, 2], [3, 2, 2, 3], [4, 3, 3, 2]]
>>> print(EditDistancePath.OP)
[['', 'I', 'I', 'I'], ['D', 'S', 'DS', 'DS'], ['D', 'M', 'DS', 'M'], ['D', 'I', 'S', 'DIS'], ['D', 'IM', 'IS', 'M']]
>>> exit()
|
Program of Edit Distance (java)
Consider a program that calculates the edit distance between two strings.
In the following program, the array cost is
"the minimum cost to reach each state"
and the array parent records "the most recent operation to reach that state with the minimum cost".
Since each type of operation is represented by a different bit, even multiple operations can be recorded at the same time.
- MATCH ... the rightmost bit ($2^0 = 1$)
- SUBSTITUTE ... 2nd bit from th right ($2^1 = 2$)
- INSERT ... 3rd bit from the right ($2^2 = 4$)
- DELETE ... 右から4番目のbit (= 8) ($2^3 = 8$)
For example, if the operation is "$SI$" (= SUBSTITUTE or INSERT),
the operations are recorded as $2+4=6$.
For simplicity, only one operation sequence of the minimal cost is shown, even if there are multiple.
| EditDistance.java |
import java.util.*;
public class EditDistance {
int COST_M = 0, COST_S = 1, COST_D = 1, COST_I = 1;
public static final int OP_M = 1, OP_S = 2, OP_I = 4, OP_D = 8;
String s,t;
int[][] cost, op;
public EditDistance(String s,String t) { this.s = s; this.t = t; }
public void setSubstituteCost(int COST_S) { this.COST_S = COST_S; }
public void setInsertCost(int COST_I) { this.COST_I = COST_I; }
public void setDeleteCost(int COST_D) { this.COST_D = COST_D; }
public int solve() {
cost = new int[s.length()+1][t.length()+1];
cost[0][0] = 0;
op = new int[s.length()+1][t.length()+1];
op[0][0] = 0;
for (int i=1; i<cost.length; i++) {
cost[i][0] = cost[i-1][0] + COST_D;
op[i][0] = OP_D;
}
for (int i=1; i<cost[0].length; i++) {
cost[0][i] = cost[0][i-1] + COST_I;
op[0][i] = OP_I;
}
for (int si=1; si<cost.length; si++) {
for (int ti=1; ti<cost[0].length; ti++) {
int c_m = (s.charAt(si-1) == t.charAt(ti-1)) ? cost[si-1][ti-1] + COST_M : Integer.MAX_VALUE;
int c_s = cost[si-1][ti-1] + COST_S;
int c_i = cost[si][ti-1] + COST_I;
int c_d = cost[si-1][ti] + COST_D;
cost[si][ti] = Math.min(c_m,Math.min(c_s,Math.min(c_i,c_d)));
op[si][ti] = 0;
if (cost[si][ti] == c_m) op[si][ti] |= OP_M;
if (cost[si][ti] == c_s) op[si][ti] |= OP_S;
if (cost[si][ti] == c_i) op[si][ti] |= OP_I;
if (cost[si][ti] == c_d) op[si][ti] |= OP_D;
}
}
return cost[s.length()][t.length()];
}
public String[] getPath() {
ArrayList<String> v = new ArrayList<String>();
int si=cost.length-1;
int ti=cost[0].length-1;
while (si > 0 || ti > 0) {
if ((op[si][ti] & OP_M) != 0) {
v.add("matches '"+s.charAt(si-1)+"' and '"+t.charAt(ti-1)+"'");
si--; ti--;
} else if ((op[si][ti] & OP_S) != 0) {
v.add("substitute '"+s.charAt(si-1)+"' by '"+t.charAt(ti-1)+"'");
si--; ti--;
} else if ((op[si][ti] & OP_I) != 0) {
v.add("insert '"+t.charAt(ti-1)+"'");
ti--;
} else if ((op[si][ti] & OP_D) != 0) {
v.add("delete '"+s.charAt(si-1)+"'");
si--;
} else throw new RuntimeException("bad op");
}
Collections.reverse(v);
return v.toArray(new String[0]);
}
public String showCostTable() { return toString(cost); }
public String showOpTable() { return toString(op); }
public String toString(int[][] x) {
StringBuilder sb = new StringBuilder(" | ");
for (int i=0; i<t.length(); i++) sb.append(" "+t.charAt(i));
int w = sb.toString().length();
sb.append("\n");
for (int i=0; i<w; i++) sb.append((i==1) ? "+" : "-");
sb.append("\n");
for (int line=0; line < x.length; line++) {
if (line == 0) sb.append(" | ");
else sb.append(s.charAt(line-1)+"| ");
for (int col=0; col < x[line].length; col++) {
int v=x[line][col];
if (v < 10 && v>=0) sb.append(" ");
sb.append(v + " ");
}
sb.append("\n");
}
return sb.toString();
}
}
|
| RunEditDistance.java |
/*
* [Usage]
* $ java RunEditDistance saka ara
*/
import java.util.*;
public class RunEditDistance {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s,t;
if (args.length > 0) s=args[0];
else { System.out.print("s="); s = sc.next();}
if (args.length > 1) t=args[1];
else { System.out.print("t="); t = sc.next();}
EditDistance ed = new EditDistance(s,t);
System.out.println(ed.solve());
System.out.println(ed.showCostTable());
System.out.println(ed.showOpTable());
String[] a = ed.getPath();
for (int i=0; i<a.length; i++)
System.out.println(a[i]);
}
}
|
| RunEditDistance.javaの実行例 |
$ javac RunEditDistance.java EditDistance.java
$ java RunEditDistance "saka" "ara"
2
| a r a
-+------------
| 0 1 2 3
s| 1 1 2 3
a| 2 1 2 2
k| 3 2 2 3
a| 4 3 3 2
| a r a
-+------------
| 0 4 4 4
s| 8 2 6 6
a| 8 1 6 1
k| 8 8 2 14
a| 8 9 10 1
delete 's'
matches 'a' and 'a'
substitute 'k' by 'r'
matches 'a' and 'a'
$ java RunEditDistance "apple is good" "applet is god"
2
| a p p l e t i s g o d
-+------------------------------------------
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13
a| 1 0 1 2 3 4 5 6 7 8 9 10 11 12
p| 2 1 0 1 2 3 4 5 6 7 8 9 10 11
p| 3 2 1 0 1 2 3 4 5 6 7 8 9 10
l| 4 3 2 1 0 1 2 3 4 5 6 7 8 9
e| 5 4 3 2 1 0 1 2 3 4 5 6 7 8
| 6 5 4 3 2 1 1 1 2 3 4 5 6 7
i| 7 6 5 4 3 2 2 2 1 2 3 4 5 6
s| 8 7 6 5 4 3 3 3 2 1 2 3 4 5
| 9 8 7 6 5 4 4 3 3 2 1 2 3 4
g| 10 9 8 7 6 5 5 4 4 3 2 1 2 3
o| 11 10 9 8 7 6 6 5 5 4 3 2 1 2
o| 12 11 10 9 8 7 7 6 6 5 4 3 2 2
d| 13 12 11 10 9 8 8 7 7 6 5 4 3 2
| a p p l e t i s g o d
-+------------------------------------------
| 0 4 4 4 4 4 4 4 4 4 4 4 4 4
a| 8 1 4 4 4 4 4 4 4 4 4 4 4 4
p| 8 8 1 5 4 4 4 4 4 4 4 4 4 4
p| 8 8 9 1 4 4 4 4 4 4 4 4 4 4
l| 8 8 8 8 1 4 4 4 4 4 4 4 4 4
e| 8 8 8 8 8 1 4 4 4 4 4 4 4 4
| 8 8 8 8 8 8 2 1 4 4 5 4 4 4
i| 8 8 8 8 8 8 10 10 1 4 4 4 4 4
s| 8 8 8 8 8 8 10 10 8 1 4 4 4 4
| 8 8 8 8 8 8 10 1 8 8 1 4 4 4
g| 8 8 8 8 8 8 10 8 10 8 8 1 4 4
o| 8 8 8 8 8 8 10 8 10 8 8 8 1 4
o| 8 8 8 8 8 8 10 8 10 8 8 8 9 2
d| 8 8 8 8 8 8 10 8 10 8 8 8 8 1
matches 'a' and 'a'
matches 'p' and 'p'
matches 'p' and 'p'
matches 'l' and 'l'
matches 'e' and 'e'
insert 't'
matches ' ' and ' '
matches 'i' and 'i'
matches 's' and 's'
matches ' ' and ' '
matches 'g' and 'g'
delete 'o'
matches 'o' and 'o'
matches 'd' and 'd'
$ java RunEditDistance "thou shalt not" "you should not"
5
| y o u s h o u l d n o t
-+---------------------------------------------
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
t| 1 1 2 3 4 5 6 7 8 9 10 11 12 13 13
h| 2 2 2 3 4 5 5 6 7 8 9 10 11 12 13
o| 3 3 2 3 4 5 6 5 6 7 8 9 10 11 12
u| 4 4 3 2 3 4 5 6 5 6 7 8 9 10 11
| 5 5 4 3 2 3 4 5 6 6 7 7 8 9 10
s| 6 6 5 4 3 2 3 4 5 6 7 8 8 9 10
h| 7 7 6 5 4 3 2 3 4 5 6 7 8 9 10
a| 8 8 7 6 5 4 3 3 4 5 6 7 8 9 10
l| 9 9 8 7 6 5 4 4 4 4 5 6 7 8 9
t| 10 10 9 8 7 6 5 5 5 5 5 6 7 8 8
| 11 11 10 9 8 7 6 6 6 6 6 5 6 7 8
n| 12 12 11 10 9 8 7 7 7 7 7 6 5 6 7
o| 13 13 12 11 10 9 8 7 8 8 8 7 6 5 6
t| 14 14 13 12 11 10 9 8 8 9 9 8 7 6 5
| y o u s h o u l d n o t
-+---------------------------------------------
| 0 4 4 4 4 4 4 4 4 4 4 4 4 4 4
t| 8 2 6 6 6 6 6 6 6 6 6 6 6 6 1
h| 8 10 2 6 6 6 1 4 4 4 4 4 4 4 4
o| 8 10 1 6 6 6 14 1 4 4 4 4 4 5 4
u| 8 10 8 1 4 4 4 12 1 4 4 4 4 4 4
| 8 10 8 8 1 4 4 4 12 2 6 1 4 4 4
s| 8 10 8 8 8 1 4 4 4 4 6 14 2 6 6
h| 8 10 8 8 8 8 1 4 4 4 4 4 4 6 6
a| 8 10 8 8 8 8 8 2 6 6 6 6 6 6 6
l| 8 10 8 8 8 8 8 10 2 1 4 4 4 4 4
t| 8 10 8 8 8 8 8 10 10 10 2 6 6 6 1
| 8 10 8 8 9 8 8 10 10 10 10 1 4 4 4
n| 8 10 8 8 8 8 8 10 10 10 10 8 1 4 4
o| 8 10 9 8 8 8 8 1 14 10 10 8 8 1 4
t| 8 10 8 8 8 8 8 8 2 14 10 8 8 8 1
delete 't'
substitute 'h' by 'y'
matches 'o' and 'o'
matches 'u' and 'u'
matches ' ' and ' '
matches 's' and 's'
matches 'h' and 'h'
insert 'o'
substitute 'a' by 'u'
matches 'l' and 'l'
substitute 't' by 'd'
matches ' ' and ' '
matches 'n' and 'n'
matches 'o' and 'o'
matches 't' and 't'
|
Exercise
Exercise a
| Submission File | EditDistance.java |
|---|
| Comment:
|
Minimum cost of editing the original string
"sushi and wine belong to food"
to the target string
"sun shines and window blows, good"
|
|---|
| Submit to: |
|
|---|
Assume that the cost of SUBSTITUTE, INSERT, DELETE and MATCH operations are $1$, $1$, $1$, $0$, respectively.
Find the minimum cost to edit from the original string
"sushi and wine belong to food"
to the target string
"sun shines and window blows, good".
Exercise b
| NearWord.java |
| Comment:
|
Note that the input dataset is different for each student.
The input dataset is assigned by the result of modulo 3 of the last digit of the student number.
Paste the output of the program for each input data.
(Paste the 7 execution result).
| Group 0 | Group 1 | Group 2 |
|---|
abcense
explasion
foorin
irerebant
nowlege
rigitemite
newclear
|
akcept
exagelat
forine
embaras
misaile
gaard
okacionally
|
colligion
forhedd
riblaly
haight
hipoksicy
laiing
brouchere
|
|
|---|
| Submit to: |
|
|---|
Write a program that points out typos in English and suggests correct words.
However, it must meet the following specifications.
- User input should be one line. You can include whitespace characters in the input
- Use mwords_74550common.txt as a dictionary.
- To find the "line in the dictionary" that has the minimum edit distance to the input
- The first line of the output is the mininum edit distance.
The second and subsequent lines should be "the dictinary line with the minimum edit distance".
- If there are multiple solutions, list all solutions, on per line.
- SUBSTITUTE, INSERT, DELETE of MATCH cost are
$1$, $1$, $1$ and $0$, respectively.
The contents of
"mwords_74550common.txt"
are take from the list of 74550 words
including in several dictionaries
which is
available from
Grady Ward's Moby Project
http://icon.shef.ac.uk/Moby/mwords.html
.
| Part of "mwords_74550common.txt" |
...(omitted)...
alow
alp
alpaca
alpenglow
alpenhorn
alpenstock
alpestrine
alpha
alpha and omega
alpha decay
...(omitted)...
|
| NearWord.java |
import java.util.*;
import java.io.*;
public class NearWord {
private Vector<String> dic;
private int minCost;
public NearWord(String fname) {
try {
Scanner sc = new Scanner(new File(fname));
dic = new Vector<String>();
while (sc.hasNext())
dic.add(sc.nextLine());
} catch (Exception e) {
e.printStackTrace();
System.exit(-1);
}
}
public int cost() { return minCost; }
public Vector<String> find(String s) {
minCost = Integer.MAX_VALUE;
// [Exercise] Write the appropriate code hear.
}
public static void main(String[] args) {
NearWord nw = new NearWord("mwords_74550common.txt");
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
Vector<String> words = nw.find(s);
System.out.println(nw.cost());
for (String w: words)
System.out.println(w);
}
}
|
| Execution log of NearWord.java |
$ javac NearWord.java
$ java NearWord
Amanda's applet
5
Adam's apple
$ java NearWord
womin
1
woman
women
$ java NearWord
thiatar
2
theater
$ java NearWord
the Internet
6
eterne
herb bennet
interne
internee
phenanthrene
tenter
theater
theatre
|
Yoshihisa Nitta
http://nw.tsuda.ac.jp/