Levenshtein Distance, Edit Distance

Algorithm (アルゴリズム)

Dynamic Programming (動的計画法)

Levenshtein distance (レーベンシュタイン距離) / Edit Distance (編集距離)

「ある文字列 s と別の文字列 t がどれだけ似ているか」を判断したい場合があります。それを表すのが編集距離 (Edit Distance) という概念です (レーベンシュタイン距離, Levenshtein distance とも言います)。編集距離が小さいほど「近い」、すなわち「似ている」ということになります。

文字列 s に次の3種類の操作を加えて、文字列 t に変更するにかかる手間が編集距離です。 3種類の操作それぞれにコスト(cost, 手間)が設定されるのが普通です。

置き換え(substitute) ... sの中の1文字を別の1文字で置き換える。例 apble → apple
挿入(insert) ... sの中に1文字を挿入する。例 aple → apple
削除(delete) ... sの中の1文字を削除する。例 applet → apple

編集距離を計算するためには、動的計画法を用います。長さnと長さmの文字列の間の編集距離を求めるのに$(n+1) \times (m+1)$の2次元行列の各要素を計算で求めていくので、計算量はO(mn)です。

[理解のポイント]

「表1:編集中の文字列の状態」の各セルにおける文字列の状態をよく確認して下さい。文字列の状態が

「生成した文字列」
「消費した文字列」
「カーソル位置(編集ポイント)」

という3要素から構成されていることを理解すれば、アルゴリズムの動きが容易に理解できるようになります。

編集距離の計算例

"saka"という文字列から"ara"という文字を生成するときにコストが最小となるような編集操作を考えます。文字列"saka"のうち再利用できる部分は再利用しながら消費して、なるべく効率良く文字列"ara"を生成したいわけです。

動的計画法で解くには、元の(消費すべき)文字列を縦に、生成すべき文字列を横に書いた表を用います。各文字列の先頭は一マス分空けておきます。

この表の中の各マスに対応する編集中の文字列の状態は次のようになります。

文字列を編集している位置を「カーソル位置」または「編集ポイント」とよび、'|' (vertical bar, 縦棒)で表しています。
カーソル位置の左にある文字(赤色で表現しています)は「既に生成した文字列」です
カーソル位置の右にある文字(緑色で表現しています)は「元の文字列のうちまだ消費していない文字列」です。

表1: 編集中の文字列の状態

		a	r	a
	\|saka	a\|saka	ar\|saka	ara\|saka
s	\|aka	a\|aka	ar\|aka	ara\|aka
a	\|ka	a\|ka	ar\|ka	ara\|ka
k	\|a	a\|a	ar\|a	ara\|a
a	\|	a\|	ar\|	ara\|

最小コストを求めるだけならば表は1つでいいのですが、編集操作の手順を記録しておく必要がある場合は表をもう1つ用意します。

今回の例ではそれぞれの操作のコストを以下のように仮定します。もちろんこれらの値はどのように設定しても構いません。

表2: 編集操作のコスト

操作	記号	コスト	説明
Insert	I	1	カーソル位置の左に1文字を挿入します。
Delete	D	1	カーソル位置の右の1文字を削除します
Substitute	S	1	カーソル位置の右の1文字を置き換え、右に1文字分カーソル位置を移動します
Match	M	0	カーソル位置を右に1文字分移動します

以下では、表の L行R列要素を(L,R)と表現しています。

2つの表のうち、左の表はコストを記録します。右の表は最小コストを決定したときに最後に行った操作を記録します。

左表の(0,0)にコスト0と記入しましょう。右表の(0,0)はまだ何も操作を行っていないので"-"です。

欄	操作	編集中の文字列
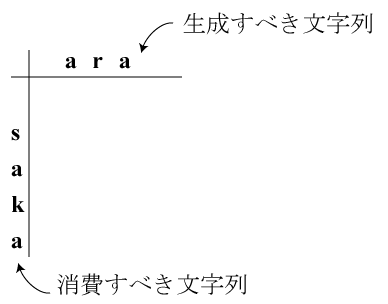
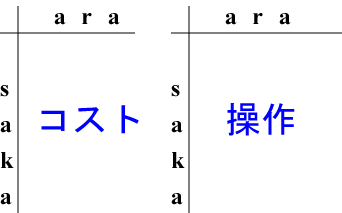
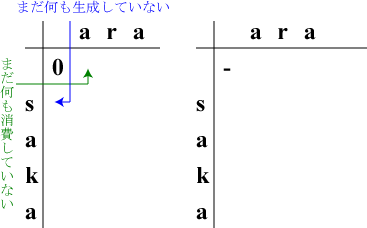
(0,0)	初期状態	\|saka

左表の最左の行の欄(L,0)に削除のコストを足しながら記入していきます。「削除」ですから右表の(L,0)には"D"と記入します。

欄	操作	編集中の文字列
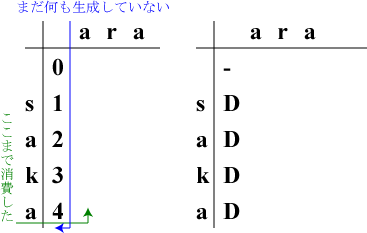
(0,0)	初期状態	\|saka
(1,0)	's'を『削除』	\|aka
(2,0)	'a'を『削除』	\|ka
(3,0)	'k'を『削除』	\|a
(4,0)	'a'を『削除』	\|

左表の最上の行の欄(0,R)に挿入のコストを足しながら記入していきます。「挿入」ですから右表の(0,R)には"I"と記入します。

欄	操作	編集中の文字列
(0,0)	初期状態	\|saka
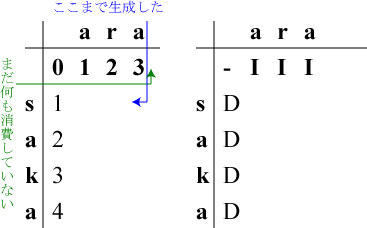
(0,1)	'a'を『挿入』	a\|saka
(0,2)	'r'を『挿入』	ar\|saka
(0,3)	'a'を『挿入』	ara\|saka

左表の(L,R)に記入すべきコストは

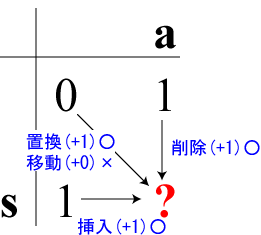
(L-1,R-1)の状態からの「置換」
(L-1,R-1)の状態からの「カーソル移動」←文字が等しい場合だけ
(L-1,R)の状態からの「削除」
(L,R-1)の状態からの「挿入」

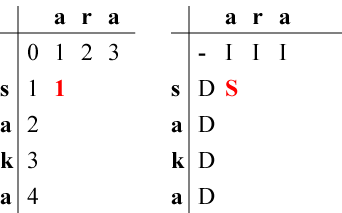
のどれかです。最小のコストを計算して左表に記入します。右表の(L,R)には選んだ操作を記入します。

左表の(1,1)の状態に到達する最小コストを考えます。カーソル位置にある文字's'と生成したい文字'a'が等しくないので「(0,0)の状態からの『カーソル移動』」は使えません。したがって、(1,1)に到達するには

「(0,0)の状態から's'を'a'に『置換』」、コストは 0+1=1
「以前に'a'を『挿入』した(0,1)の状態からの's'の『削除』」、コストは1+1=2
「以前に's'を『削除』した(1,0)の状態からの'a'の『挿入』」、コストは1+1=2

という3種類の方法がありえることがわかります。そのうち「(0,0)の状態から's'を'a'に『置換』」が最小コストで1なので、左表(1,1)には1、右表(1,1)にはS (置換, Substitute)を記入します。

欄	操作	編集中の文字列
(0,0)	初期状態	\|saka
(1,1)	's'を'a'に『置換』	a\|aka

欄(1,1)の状態は、操作の順番はともかく「『消費すべき文字列』から先頭の's'が無くなり、『生成すべき文字列』から先頭の'a'が無くなった」状態です。その状態にたどり着くための編集操作の最小コストが1であったわけです。

左表の(2,1)は、カーソル位置にある『消費すべき』文字とこれから『生成すべき文字』がどちらも'a'なのでMatchしますから「(1,0)の状態からの『カーソル移動』」が使えます。他にも「(1,1)の状態から'a'を『削除』」「(2,0)の状態から'a'を『挿入』」という方法が使えますが、左表の(2,1)に到達するには「(1,0)の状態からの『カーソル移動』」が最小コストです。左表(2,1)には1+0=1を、右表(2,1)にはM (カーソル移動, Match)を記入します。

欄	操作	編集中の文字列
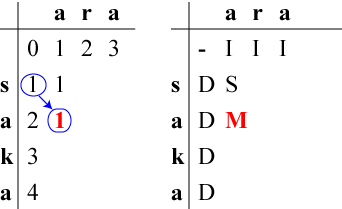
(1,0)	's'を『削除』	\|aka
(2,1)	同じ'a'なので『カーソル移動』	a\|ka

欄(2,1)の状態は、「まず『消費すべき文字列』から先頭の's'を『削除』し、その次に『消費すべき文字列』と『生成すべき文字列』がともに'a'であったので『カーソル移動』した」状態です。その状態にたどり着くための演習操作の最小コストが「削除(コスト1)」と「カーソル移動(コスト0)」の合計で、1です。

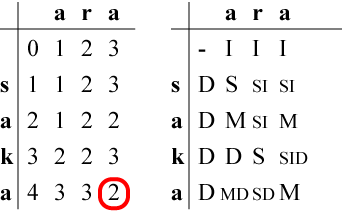
表を全て記入した状態です。

右表の中で複数の記号が併記されている場合はどちらの操作でも最小コストになることを表しています。たとえば"SI"という記号は「置換または挿入のどちらの操作でもOK」の意味です。

左表の最右下の欄である(4,3)を見ることで最小コストは2であることがわかります。

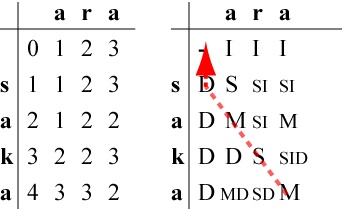
最小コストに到達する手段は、右表の右下の欄からスタートして、操作を逆に

SかMならば置換かカーソル移動によってその欄に到達したので、左上へ
Iならば挿入によってその欄に到達したので、左へ
Dならば削除されてその欄に到達したので、上へ

と辿ればわかります。

最小コストの操作手順は以下のようになります。

欄	操作	編集中の文字列
(0,0)	初期状態	\|saka
(1,0)	's'を『削除』	\|aka
(2,1)	'a'は『カーソル移動』	a\|ka
(3,2)	'k'を'r'に『置換』	ar\|a
(4,3)	'a'は『カーソル移動』	ara\|

編集距離を計算するプログラム例 (python, コストだけ)

EditDistance.py

import sys

COST_DEL = 1
COST_INS = 1
COST_SUBST = 1
COST_MATCH = 0

COST = []

def solve(s,t,flag = False):
  global COST
  sl = len(s)
  tl = len(t)
  COST = [[0 for i in range(tl+1)] for j in range(sl+1)]
  COST[0][0] = 0
  for i in range(1,sl+1):
    COST[i][0] = COST[i-1][0] + COST_DEL
  for i in range(1,tl+1):
    COST[0][i] = COST[0][i-1] + COST_INS
  for i in range(1,sl+1):
    for j in range(1,tl+1):
      c_d = COST[i][j-1] + COST_DEL
      c_i = COST[i-1][j] + COST_INS
      c_s = COST[i-1][j-1] + COST_SUBST
      if s[i-1]==t[j-1]: c_m = COST[i-1][j-1] + COST_MATCH
      else: c_m = sys.maxsize
      COST[i][j] = min(c_d, c_i, c_s, c_m)
  return COST[sl][tl]

EditDistance.pyの実行例

$ python  
Python 3.9.13 (main, Aug 25 2022, 23:26:10) 
[GCC 11.2.0] :: Anaconda, Inc. on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import EditDistance  
>>> EditDistance.solve('saka','ara')  
2
>>> print(EditDistance.COST)  
[[0, 1, 2, 3], [1, 1, 2, 3], [2, 1, 2, 2], [3, 2, 2, 3], [4, 3, 3, 2]]
>>> exit()

編集距離を計算するプログラム例 (python, コストと編集手順)

EditDistancePath.py

import sys

COST_DEL = 1
COST_INS = 1
COST_SUBST = 1
COST_MATCH = 0

COST = []
OP = []

def solve(s,t):
  global COST, OP
  sl = len(s)
  tl = len(t)
  COST = [[0 for i in range(tl+1)] for j in range(sl+1)]
  OP = [['' for i in range(tl+1)] for j in range(sl+1)]
  COST[0][0] = 0
  for i in range(1,sl+1):
    COST[i][0] = COST[i-1][0] + COST_DEL
    OP[i][0] += 'D'
  for i in range(1,tl+1):
    COST[0][i] = COST[0][i-1] + COST_INS
    OP[0][i] += 'I'
  for i in range(1,sl+1):
    for j in range(1,tl+1):
      c_d = COST[i][j-1] + COST_DEL
      c_i = COST[i-1][j] + COST_INS
      c_s = COST[i-1][j-1] + COST_SUBST
      if s[i-1]==t[j-1]: c_m = COST[i-1][j-1] + COST_MATCH
      else: c_m = sys.maxsize
      COST[i][j] = min(c_d, c_i, c_s, c_m)
      if (c_d == COST[i][j]): OP[i][j] += 'D'
      if (c_i == COST[i][j]): OP[i][j] += 'I'
      if (c_s == COST[i][j]): OP[i][j] += 'S'
      if (c_m == COST[i][j]): OP[i][j] += 'M'
  return COST[sl][tl], getPath(s,t)

def getPath(s,t):
  global OP
  r = []
  row = len(s)
  col = len(t)
  while row > 0 or col > 0:
    s_ch = s[row-1]
    t_ch = t[col-1]
    if  'M' in OP[row][col]:
      r.append('MATCH '+s_ch)
      row -= 1
      col -= 1
    elif 'S' in OP[row][col]:
      r.append('SUBSTITUTE '+s_ch+' with '+t_ch)
      row -= 1
      col -= 1
    elif 'I' in OP[row][col]:
      r.append('INSERT '+t_ch)
      col -= 1
    elif 'D' in OP[row][col]:
      r.append('DELETE '+s_ch)
      row -= 1
  r.reverse()
  return r

EditDistancePath.pyの実行例

$ python  
Python 3.9.13 (main, Aug 25 2022, 23:26:10) 
[GCC 11.2.0] :: Anaconda, Inc. on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import EditDistancePath  
>>> EditDistancePath.solve('saka','ara')  
(2, ['DELETE s', 'MATCH a', 'SUBSTITUTE k with r', 'MATCH a'])
>>> print(EditDistancePath.COST)  
[[0, 1, 2, 3], [1, 1, 2, 3], [2, 1, 2, 2], [3, 2, 2, 3], [4, 3, 3, 2]]
>>> print(EditDistancePath.OP)  
[['', 'I', 'I', 'I'], ['D', 'S', 'DS', 'DS'], ['D', 'M', 'DS', 'M'], ['D', 'I', 'S', 'DIS'], ['D', 'IM', 'IS', 'M']]
>>> exit()

編集距離を計算するプログラム例 (java)

2つの文字列の編集距離を計算するプログラムを考えましょう。

次のプログラムでは、配列 cost に「それぞれの状態に至る最小コスト」を記録し、配列 parent に「その状態に最小コストで到達するための直近の操作」を記録します。操作を種類毎に異なるbitで表現しているので、複数の操作でも同時に記録できます。

MATCH ... 最も右の 1bit (= 1)
SUBSTITUTE ... 右から2番目のbit (= 2)
INSERT ... 右から3番目のbit (= 4)
DELETE ... 右から4番目のbit (= 8)

たとえば手順が SI (SUBSTITUTEまたはINSERT)の場合は 2+4で 6と記録されます。

簡単のため、最小コストの編集手順はたとえ複数存在しても一通りだけ表示するようにしています。

EditDistance.java

import java.util.*;
public class EditDistance {
    int COST_M = 0, COST_S = 1, COST_D = 1, COST_I = 1;
    public static final int OP_M = 1, OP_S = 2, OP_I = 4, OP_D = 8;
    String s,t;
    int[][] cost, op;
    public EditDistance(String s,String t) { this.s = s; this.t = t; }
    public void setSubstituteCost(int COST_S) { this.COST_S = COST_S; }
    public void setInsertCost(int COST_I) { this.COST_I = COST_I; }
    public void setDeleteCost(int COST_D) { this.COST_D = COST_D; }
    public int solve() {
	cost = new int[s.length()+1][t.length()+1];
	cost[0][0] = 0;
	op = new int[s.length()+1][t.length()+1];
	op[0][0] = 0;
	for (int i=1; i<cost.length; i++) {
	    cost[i][0] = cost[i-1][0] + COST_D;
	    op[i][0] = OP_D;
	}
	for (int i=1; i<cost[0].length; i++) {
	    cost[0][i] = cost[0][i-1] + COST_I;
	    op[0][i] = OP_I;
	}
	for (int si=1; si<cost.length; si++) {
	    for (int ti=1; ti<cost[0].length; ti++) {
		int c_m = (s.charAt(si-1) == t.charAt(ti-1)) ? cost[si-1][ti-1] + COST_M : Integer.MAX_VALUE;
		int c_s = cost[si-1][ti-1] + COST_S;
		int c_i = cost[si][ti-1] + COST_I;
		int c_d = cost[si-1][ti] + COST_D;
		cost[si][ti] = Math.min(c_m,Math.min(c_s,Math.min(c_i,c_d)));
		op[si][ti] = 0;
		if (cost[si][ti] == c_m) op[si][ti] |= OP_M;
		if (cost[si][ti] == c_s) op[si][ti] |= OP_S;
		if (cost[si][ti] == c_i) op[si][ti] |= OP_I;
		if (cost[si][ti] == c_d) op[si][ti] |= OP_D;
	    }
	}
	return cost[s.length()][t.length()];
    }
    public String[] getPath() {
	ArrayList<String> v = new ArrayList<String>();
	int si=cost.length-1;
	int ti=cost[0].length-1;
	while (si > 0 || ti > 0) {
	    if ((op[si][ti] & OP_M) != 0) {
		v.add("matches '"+s.charAt(si-1)+"' and '"+t.charAt(ti-1)+"'");
		si--; ti--;
	    } else if ((op[si][ti] & OP_S) != 0) {
		v.add("substitute '"+s.charAt(si-1)+"' by '"+t.charAt(ti-1)+"'");
		si--; ti--;
	    } else if ((op[si][ti] & OP_I) != 0) {
		v.add("insert '"+t.charAt(ti-1)+"'");
		ti--;
	    } else if ((op[si][ti] & OP_D) != 0) {
		v.add("delete '"+s.charAt(si-1)+"'");
		si--;
	    } else throw new RuntimeException("bad op");
	}
	Collections.reverse(v);
	return v.toArray(new String[0]);
    }
    public String showCostTable() { return toString(cost); }
    public String showOpTable() { return toString(op); }
    public String toString(int[][] x) {
	StringBuilder sb = new StringBuilder(" |   ");
	for (int i=0; i<t.length(); i++) sb.append("  "+t.charAt(i));
	int w = sb.toString().length();
	sb.append("\n");
	for (int i=0; i<w; i++) sb.append((i==1) ? "+" : "-");
	sb.append("\n");
	for (int line=0; line < x.length; line++) {
	    if (line == 0) sb.append(" | ");
	    else sb.append(s.charAt(line-1)+"| ");
	    for (int col=0; col < x[line].length; col++) {
		int v=x[line][col];
		if (v < 10 && v>=0) sb.append(" ");
		sb.append(v + " ");
	    }
	    sb.append("\n");
	}
	return sb.toString();
    }
}

RunEditDistance.java

/*
 * [Usage]
 * $ java RunEditDistance saka ara
 */
import java.util.*;
public class RunEditDistance {
    public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	String s,t;
	if (args.length > 0) s=args[0];
	else { System.out.print("s="); s = sc.next();}
	if (args.length > 1) t=args[1];
	else { System.out.print("t="); t = sc.next();}
	
	EditDistance ed = new EditDistance(s,t);
	System.out.println(ed.solve());
	System.out.println(ed.showCostTable());
	System.out.println(ed.showOpTable());
	String[] a = ed.getPath();
	for (int i=0; i<a.length; i++)
	    System.out.println(a[i]);
    }
}

RunEditDistance.javaの実行例

$ javac RunEditDistance.java EditDistance.java
$ java RunEditDistance "saka" "ara"
2
 |     a  r  a
-+------------
 |  0  1  2  3 
s|  1  1  2  3 
a|  2  1  2  2 
k|  3  2  2  3 
a|  4  3  3  2 

 |     a  r  a
-+------------
 |  0  4  4  4 
s|  8  2  6  6 
a|  8  1  6  1 
k|  8  8  2 14 
a|  8  9 10  1 

delete 's'
matches 'a' and 'a'
substitute 'k' by 'r'
matches 'a' and 'a'

$ java RunEditDistance "apple is good" "applet is god"
2
 |     a  p  p  l  e  t     i  s     g  o  d
-+------------------------------------------
 |  0  1  2  3  4  5  6  7  8  9 10 11 12 13 
a|  1  0  1  2  3  4  5  6  7  8  9 10 11 12 
p|  2  1  0  1  2  3  4  5  6  7  8  9 10 11 
p|  3  2  1  0  1  2  3  4  5  6  7  8  9 10 
l|  4  3  2  1  0  1  2  3  4  5  6  7  8  9 
e|  5  4  3  2  1  0  1  2  3  4  5  6  7  8 
 |  6  5  4  3  2  1  1  1  2  3  4  5  6  7 
i|  7  6  5  4  3  2  2  2  1  2  3  4  5  6 
s|  8  7  6  5  4  3  3  3  2  1  2  3  4  5 
 |  9  8  7  6  5  4  4  3  3  2  1  2  3  4 
g| 10  9  8  7  6  5  5  4  4  3  2  1  2  3 
o| 11 10  9  8  7  6  6  5  5  4  3  2  1  2 
o| 12 11 10  9  8  7  7  6  6  5  4  3  2  2 
d| 13 12 11 10  9  8  8  7  7  6  5  4  3  2 

 |     a  p  p  l  e  t     i  s     g  o  d
-+------------------------------------------
 |  0  4  4  4  4  4  4  4  4  4  4  4  4  4 
a|  8  1  4  4  4  4  4  4  4  4  4  4  4  4 
p|  8  8  1  5  4  4  4  4  4  4  4  4  4  4 
p|  8  8  9  1  4  4  4  4  4  4  4  4  4  4 
l|  8  8  8  8  1  4  4  4  4  4  4  4  4  4 
e|  8  8  8  8  8  1  4  4  4  4  4  4  4  4 
 |  8  8  8  8  8  8  2  1  4  4  5  4  4  4 
i|  8  8  8  8  8  8 10 10  1  4  4  4  4  4 
s|  8  8  8  8  8  8 10 10  8  1  4  4  4  4 
 |  8  8  8  8  8  8 10  1  8  8  1  4  4  4 
g|  8  8  8  8  8  8 10  8 10  8  8  1  4  4 
o|  8  8  8  8  8  8 10  8 10  8  8  8  1  4 
o|  8  8  8  8  8  8 10  8 10  8  8  8  9  2 
d|  8  8  8  8  8  8 10  8 10  8  8  8  8  1 

matches 'a' and 'a'
matches 'p' and 'p'
matches 'p' and 'p'
matches 'l' and 'l'
matches 'e' and 'e'
insert 't'
matches ' ' and ' '
matches 'i' and 'i'
matches 's' and 's'
matches ' ' and ' '
matches 'g' and 'g'
delete 'o'
matches 'o' and 'o'
matches 'd' and 'd'

$ java RunEditDistance "thou shalt not" "you should not"
5
 |     y  o  u     s  h  o  u  l  d     n  o  t
-+---------------------------------------------
 |  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 
t|  1  1  2  3  4  5  6  7  8  9 10 11 12 13 13 
h|  2  2  2  3  4  5  5  6  7  8  9 10 11 12 13 
o|  3  3  2  3  4  5  6  5  6  7  8  9 10 11 12 
u|  4  4  3  2  3  4  5  6  5  6  7  8  9 10 11 
 |  5  5  4  3  2  3  4  5  6  6  7  7  8  9 10 
s|  6  6  5  4  3  2  3  4  5  6  7  8  8  9 10 
h|  7  7  6  5  4  3  2  3  4  5  6  7  8  9 10 
a|  8  8  7  6  5  4  3  3  4  5  6  7  8  9 10 
l|  9  9  8  7  6  5  4  4  4  4  5  6  7  8  9 
t| 10 10  9  8  7  6  5  5  5  5  5  6  7  8  8 
 | 11 11 10  9  8  7  6  6  6  6  6  5  6  7  8 
n| 12 12 11 10  9  8  7  7  7  7  7  6  5  6  7 
o| 13 13 12 11 10  9  8  7  8  8  8  7  6  5  6 
t| 14 14 13 12 11 10  9  8  8  9  9  8  7  6  5 

 |     y  o  u     s  h  o  u  l  d     n  o  t
-+---------------------------------------------
 |  0  4  4  4  4  4  4  4  4  4  4  4  4  4  4 
t|  8  2  6  6  6  6  6  6  6  6  6  6  6  6  1 
h|  8 10  2  6  6  6  1  4  4  4  4  4  4  4  4 
o|  8 10  1  6  6  6 14  1  4  4  4  4  4  5  4 
u|  8 10  8  1  4  4  4 12  1  4  4  4  4  4  4 
 |  8 10  8  8  1  4  4  4 12  2  6  1  4  4  4 
s|  8 10  8  8  8  1  4  4  4  4  6 14  2  6  6 
h|  8 10  8  8  8  8  1  4  4  4  4  4  4  6  6 
a|  8 10  8  8  8  8  8  2  6  6  6  6  6  6  6 
l|  8 10  8  8  8  8  8 10  2  1  4  4  4  4  4 
t|  8 10  8  8  8  8  8 10 10 10  2  6  6  6  1 
 |  8 10  8  8  9  8  8 10 10 10 10  1  4  4  4 
n|  8 10  8  8  8  8  8 10 10 10 10  8  1  4  4 
o|  8 10  9  8  8  8  8  1 14 10 10  8  8  1  4 
t|  8 10  8  8  8  8  8  8  2 14 10  8  8  8  1 

delete 't'
substitute 'h' by 'y'
matches 'o' and 'o'
matches 'u' and 'u'
matches ' ' and ' '
matches 's' and 's'
matches 'h' and 'h'
insert 'o'
substitute 'a' by 'u'
matches 'l' and 'l'
substitute 't' by 'd'
matches ' ' and ' '
matches 'n' and 'n'
matches 'o' and 'o'
matches 't' and 't'

演習

課題a

提出ファイル	EditDistance.java
コメント欄:	文字列 "sushi and wine belong to food" を編集して文字列 "sun shines and window blows, good" を生成する場合の最小コスト
提出先:

Substitute, Insert, Delete, Matchそれぞれの文字列操作のコストが1,1,1,0であるとする。文字列 "sushi and wine belong to food" を編集して文字列 "sun shines and window blows, good" を生成する場合の最小コストを求めよ。

課題b

提出ファイル

NearWord.java

コメント欄:

学生ごとに入力データセットが異なるので注意が必要である。学生番号の末尾の数字を３で割った余りで入力データセットが割り当てられる。割り当てられたデータをプログラムで処理した結果の出力をコメント欄に貼り付けておくこと。 (1度に1個の入力データを処理した、合計7回分の実行結果を貼り付けること）。

グループ0	グループ1	グループ2
abcense explasion foorin irerebant nowlege rigitemite newclear	akcept exagelat forine embaras misaile gaard okacionally	colligion forhedd riblaly haight hipoksicy laiing brouchere

提出先:

「英単語のタイプミスを指摘し、正しい単語の候補を示す」プログラムを作りなさい。ただし、以下の仕様を満たすこと。

ユーザの入力は1行とする。途中に空白文字を含んでもよい。
辞書として mwords_74550common.txt を用いる。
「ユーザが入力した行」と最も編集距離が近い「辞書中の行」を発見すること。
出力の最初の行が「最小の編集距離」、 2行目以降は「最も編集距離が短い行の内容」であること。
解が複数ある場合は、全ての解を1行に１つずつ表示すること。
文字列操作 Substitute, Insert, Delete, Match のコストはそれぞれ1,1,1,0とする。

"mwords_74550common.txt"の内容は Grady Ward's Moby Project http://icon.shef.ac.uk/Moby/mwords.html から入手できる単語のリストのうちの "74550com.mon" (複数の辞書に含まれる一般的な単語 74550 語)である。

mwords_74550common.txtの内容(抜粋)

...(略)...
alow
alp
alpaca
alpenglow
alpenhorn
alpenstock
alpestrine
alpha
alpha and omega
alpha decay
...(略)...

NearWord.java

import java.util.*;
import java.io.*;

public class NearWord {
    private Vector<String> dic;
    private int minCost;
    public NearWord(String fname) {
	try {
	    Scanner sc = new Scanner(new File(fname));
	    dic = new Vector<String>();
	    while (sc.hasNext())
		dic.add(sc.nextLine());
	} catch (Exception e) {
	    e.printStackTrace();
	    System.exit(-1);
	}
    }
    public int cost() { return minCost; }
    public Vector<String> find(String s) {
	minCost = Integer.MAX_VALUE;

	// [課題] ここに入るべきコードを書きなさい。

    }
    public static void main(String[] args) {
	NearWord nw = new NearWord("mwords_74550common.txt");
	Scanner sc = new Scanner(System.in);
	String s = sc.nextLine();
	Vector<String> words = nw.find(s);
	System.out.println(nw.cost());
	for (String w: words)
	    System.out.println(w);
    }
}

NearWord.javaの実行例

$ javac NearWord.java 
$ java NearWord 
Amanda's applet 
5
Adam's apple
$ java NearWord 
womin 
1
woman
women
$ java NearWord 
thiatar 
2
theater
$ java NearWord 
the Internet 
6
eterne
herb bennet
interne
internee
phenanthrene
tenter
theater
theatre

		a	r	a
	\|saka	a\|saka	ar\|saka	ara\|saka
s	\|aka	a\|aka	ar\|aka	ara\|aka
a	\|ka	a\|ka	ar\|ka	ara\|ka
k	\|a	a\|a	ar\|a	ara\|a
a	\|	a\|	ar\|	ara\|